
2.1 Анализ чувствительности
Проанализируем чувствительность построенного плана к возможному увеличению потребности в работниках вечером в воскресенье.
Вечером будем считать период с 15:00 до 23:00, который делится на две смены: 3 и 4.
При увеличении потребности в рабочих в 4 смену, увеличивается только количество временных работников в обозначенное время (воскресенье, 19:00-23:00), поэтому значение целевой функции увеличивается на дополнительное количество требуемых рабочих, умноженное на зарплату временного рабочего.
При увеличении потребности в рабочих в 3 смену, происходят следующие изменения плана:
+1) Изменение постоянных рабочих = 0, временных = +1, значение целевой функции += 6720. Временный рабочий добавляется в обозначенное время.
+2) Изменение постоянных рабочих = 0, временных = +2, значение целевой функции = +6720 · 2, но при этом изменилось распределение рабочих:
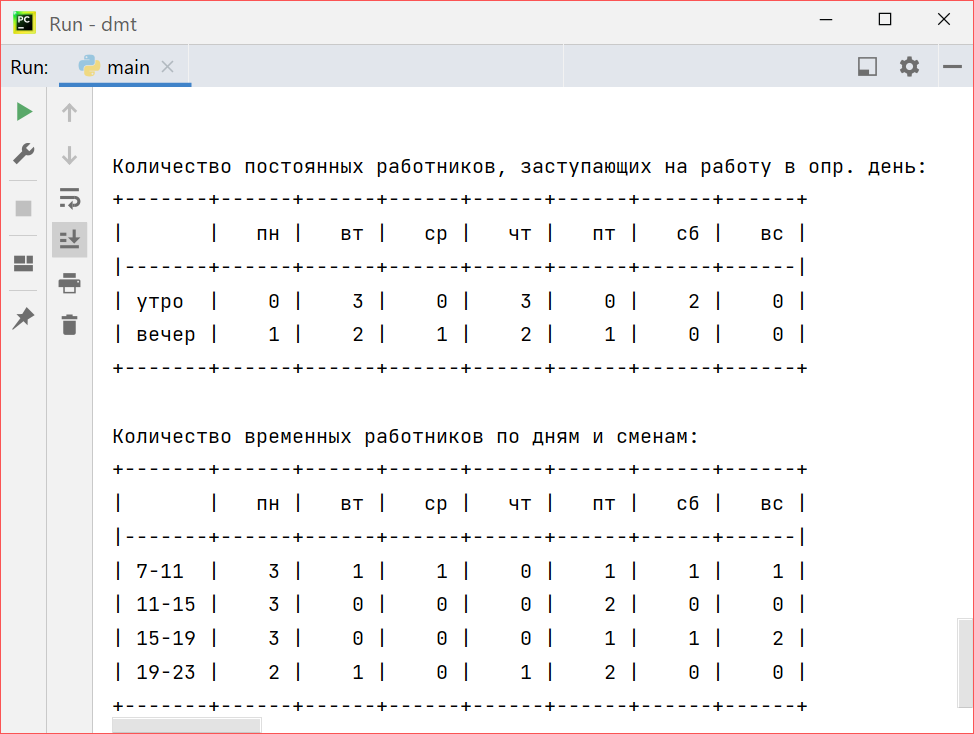
Рисунок 3 – Результаты решения при увеличении требования рабочих
+3) Изменение постоянных рабочих = 0, временных = +3, значение целевой функции = +6720 · 3, но при этом снова изменилось распределение рабочих:
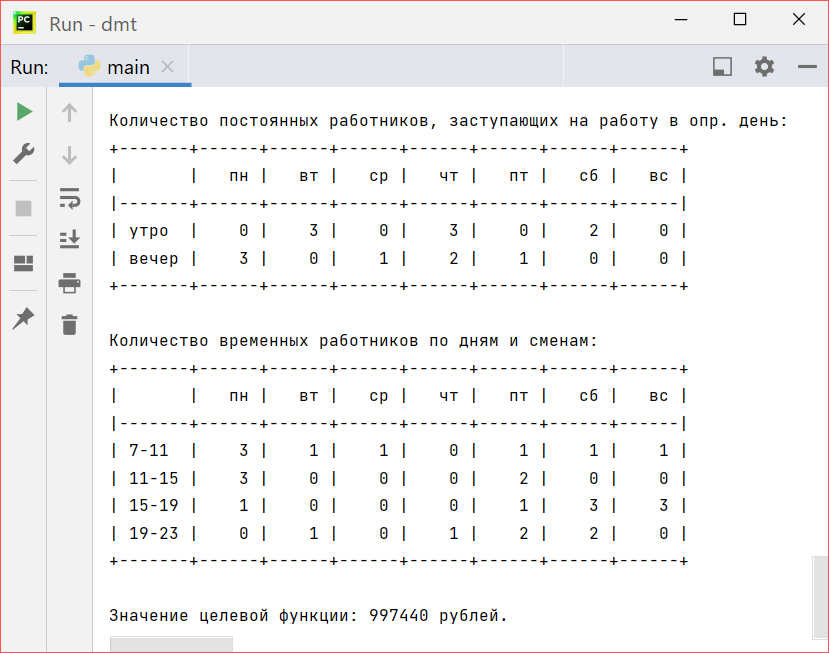
Рисунок 4 – Результаты решения при увеличении требования рабочих
При дальнейшем увеличении потребности в рабочих в период с 15:00 до 19:00 все также происходит только увеличение числа временных рабочих, но при этом больше не меняется распределение всех рабочих на неделе.
При одновременном увеличении потребности в рабочих в 3 и 4 смену происходят следующие изменения:
+1, +1) Возникают дробные числа в решении.
+2, +2) Изменение постоянных рабочих = +1, временных = -6, значение целевой функции = +14080, и изменилось распределение рабочих:
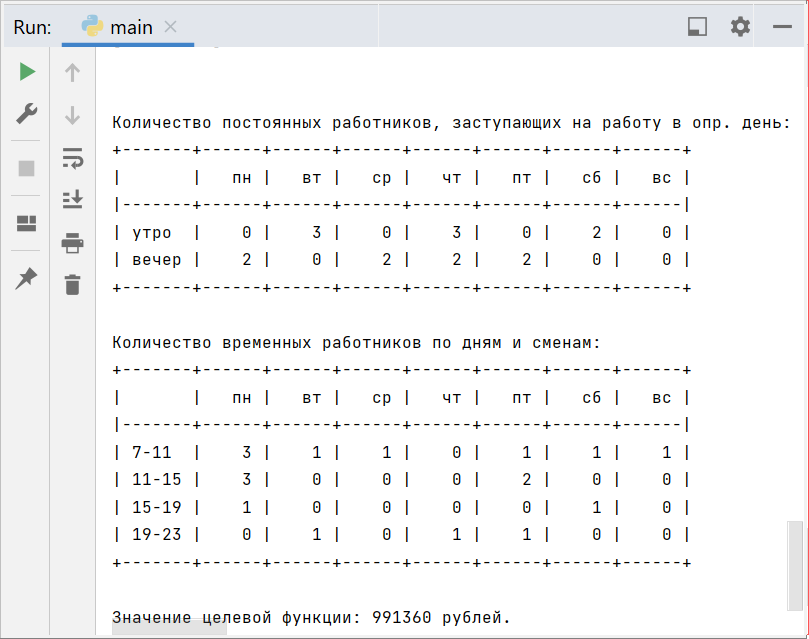
Рисунок 5 – Результаты решения при увеличении требования рабочих
В дальнейшем увеличивается лишь число временных рабочих.
Заключение
В результате решения задачи был получен оптимальный план наиболее выгодного распределения работников в течение недели. Анализ чувствительности продемонстрировал, что при увеличении потребности в рабочих в какой-то определенный день выгоднее нанимать временных работников. Это связано со сложностью распределения постоянных рабочих таким образом, чтобы они были заняты все свои рабочие часы и затраты на их зарплату окупались.
Список использованных источников
1. Пономарев А.В. Решение задач линейного программирования с использованием GNU Octave, GLPK и Python // Теория принятия решений – тематический сайт. URL: https://avponomarev.bitbucket.io/LP_tutorial.pdf (дата обращения: 25.04.2023).
2. Таха Хемди А. Введение в исследование операций. 7-е издание. М.: Издательский дом "Вильямс", 2005. - 912 с.
3. ГОСТ 7.32–2001. Межгосударственный стандарт. Отчет о научно-исследовательской работе. Структура и правила оформления. М.: Изд-во стандартов, 2001.
