Статистика учебное пособие 2012 иностр
.pdf21
1- 0.82
2- 0.28
3- 8.2
4- 2.8
7. В картотеке имеются истории болезней восьми пациентов. Если наугад взять первую, затем вторую, третью и т. д. историю болезней, то какова в каждом случае будет вероятность изъятия нужной истории болезней? Предполагается, что искомая история болезней имеется в картотеке (выберите правильные ответы).
1- 12 %
2- 8%
3- 12,5%
4- 1/8
8.В урне находится 10 шаров: 3 белых и 7 чѐрных. Из неѐ наугад извлекается один шар. Вероятность того, что этот шар будет белый равна (выберите правильные ответы)
1- Р = 3/10
2- Р = 7/10
3- Р = 3/7
4- Р = 7/3
5- Р = 30%
6- Р = 70%
9. |
В |
урне |
|
находится 10 шаров: 3 белых и 7 чѐрных. Из неѐ наугад извлекается один |
|
|
шар. Вероятность того, что этот шар будет чѐрный равна (выберите |
|
|
правильные ответы) |
|
|
1- Р = 3/10 |
|
|
2- Р = 7/10 |
|
|
3- Р = 3/7 |
|
|
4- Р = 7/3 |
|
|
5- Р = 30% |
|
|
6 - Р = 70% |
|
10. |
В |
урне |
|
находится 10 шаров: 3 белых и 7 чѐрных. Из неѐ наугад извлекается |
|
|
чѐрный шар и не возвращается в урну. Вероятность извлечь после этого |
|
белый шар равна
1- Р = 60%
2- Р = 2/3
3- Р = 0,6
4- Р = 1/3
22
11. В урне находится 10 шаров: 3 белых и 7 чѐрных. Из неѐ наугад извлекается белый шар и не возвращается в урну. Вероятность извлечь после этого чѐрный шар равна
1- Р = 70%
2- Р = 7/9
3- Р = 0,7
4- Р = 2/9
12. В урне находится 10 шаров: 3 белых и 7 чѐрных. Из неѐ наугад извлекается белый шар и не возвращается в урну. Вероятность извлечь после этого белый шар равна
1- Р = 30%
2- Р = 2/9
3- Р = 0,3
4- Р = 7/9
13. Теорема для совместных событий математически имеет вид
1. P |
m |
2. P 1 |
3. P |
PA PB PC |
|
||||
|
n |
( A и B и C ) |
|
|
|
|
|
||
4. P( A и B и C ) PA PB PC
14.Теорема для несовместных событий математически имеет вид
1. P |
m |
|
2. P 1 |
3. P |
|
PA PB PC |
|
|
|
||||||
|
n |
|
|
( A или B или C ) |
|
||
|
|
|
|
|
|
||
4. P |
PA PB PC |
|
|
||||
( A или B или C ) |
|
|
|
|
|
||
15. Вероятность, |
что |
человек здоров Р i |
= 0.9. Если группа в |
||||
количестве трех |
человек контактирует |
таким образом, что |
|||||
обеспечивается заражение, то вероятность, что каждый из них будет здоров равна:
1. Рздо р Рi Pi Pi 0.9 0.9 0.9 27. 2. Рздо р Рi 3 0.93 073.
3.Рздо р. Р3i 0.9 / 3 0.9 / 3 0.9 / 3 0.9
4.Рздо р. Рi / 3 0.9 / 3 0.3
16.Теорема сложения вероятностей определяет вероятность
1. |
совместных событий |
3. невозможных событий |
2. |
несовместных событий |
4. равновозможных событий |
17.Теорема умножения вероятностей определяет вероятность |
||
1. |
совместных событий |
3. невозможных событий |
23
2.несовместных событий 4. равновозможных событий
18.Вероятность того, что взятая наугад упаковка лекарственного препарата из некоторой партии упаковок, будет бракованной равна 0,2.
В этом случае вероятность того, что из трех взятых упаковок 2 окажутся не бракованными равна
1- 3,5324
2- 0,5411
3- 2,9167
4- 0,9573
19.На основе многолетних наблюдений вызов врача в данный дом оценивается вероятностью 0,5. Вероятность того, что в течение шести
дней произойдут четыре вызова врача равна
1- 0,350
2- 0,234
3- 2,5
4- 0,99
20.В одну из больниц поступают пациенты с четырьмя видами болезней. Многолетние наблюдения показывают, что этим группам
заболеваний соответствуют вероятности : 0,1; 0,2; 0,3; и 0,4.Для лечения заболеваний с вероятностью 0,1 и 0,2 необходимо переливание крови.
Укажите какое количество больных следует обеспечить кровью, если в течение месяца поступило 1000 больных.
1- 100 больных
2- 200 больных
3- 300 больных
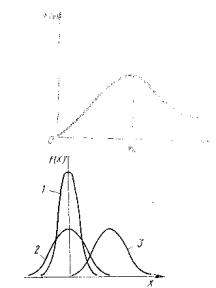
Данный график представляет 1 - распределение Гаусса 2 - распределение Максвелла
3 - распределение Больцмана
4 - распределение Пуассона
22 . Данные графики представляют
1 - распределение Гаусса
2 - распределение Максвелла
3 - распределение Больцмана
4 |
- |
распределение Пуассона
24
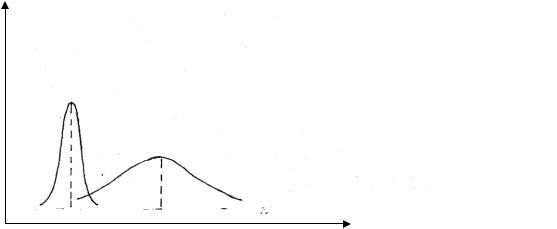
23. Укажите соответствие между М1 и М2, 1 и 2 на представленных графиках
f(x)
1.М1 >M2, 1 < 2 2. М1 = M2, 1 = 2 3. М1 < M2, 1 < 2 4. М1 <M2, 1 > 2
M1 |
M2 |
x |
24.При увеличении математического ожидания вершина кривой Гаусса
1.не смещается
2.смещается вправо
3.смещается влево
4.смещается вверх
25.Математическое ожидание при большом числе измерений равно
1.дисперсии
2.доверительной вероятности
3.среднему арифметическому значению
4.среднему квадратическому значению
26.Дисперсия показывает
1. |
отклонение х от М(х) |
3. отклонение от М(х) |
2. |
отклонение М(х) от хо |
4. отклонение от М(х) |
27. При увеличении среднеквадратического значения вершина кривой Гаусса
1.опускается вниз
2.становится более острой
3.поднимается вверх
4.становится менее острой
28. Нормальное распределение графически может быть представлено
25
1. распределением Максвелла 2. кривой Гаусса
3.кривой Больцмана
29.Формула дисперсии для распределения непрерывных случайных величин
1- M(x2) - [M(x)]2
|
|
|
|
|
|
|
|
|
|
2- |
f (x)dx |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3- |
[x M (x)]2 f (x)dx |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
2 |
2 |
|
f |
2 |
2 |
|
|
|
|
|
Sx1 |
|
|
|
Sx2 ... |
|
|
x |
x |
|||||||
4- |
|
|
|
|
|||||
|
|
1 |
|
|
|
2 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
5- |
xi pi |
|
|
|
|
|
|||
|
i 1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
6- |
xf (x)dx |
|
|
|
|
||||
30. Формула математического ожидания для распределения дискретных случайных величин
1- M(x2) - [M(x)]2
|
|
|
|
|
|
|
|
|
|
2- |
f (x)dx |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3- |
[x M (x)]2 f (x)dx |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
2 |
2 |
|
f |
2 |
2 |
|
|
|
|
|
Sx1 |
|
|
|
Sx2 ... |
|
|
x |
x |
|||||||
4- |
|
|
|
|
|||||
|
|
1 |
|
|
|
2 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
5- |
xi pi |
|
|
|
|
||||
|
i 1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
6- |
|
xf (x)dx |
|
|
|
||||
26
31. Формула вероятности для распределения непрерывных случайных величин
1. M(x2) - [M(x)]2
|
|
|
|
|
|
|
|
|
|
2. |
f (x)dx |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
[x M (x)]2 f (x)dx |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
2 |
2 |
|
f |
2 |
2 |
|
|
|
|
|
Sx1 |
|
|
|
Sx2 ... |
|
|
x |
x |
|||||||
4. |
|
|
|
|
|||||
|
|
1 |
|
|
|
2 |
|
|
|
5.xi pi
i1n
6.xf (x)dx
32. Условие нормировки для нормального распределения непрерывных случайных величин соответствует формуле
|
|
|
1- |
xf (x)dx 1 |
|
|
|
|
|
|
|
2- |
f (x)dx 1 |
|
|
|
|
|
n |
|
3- |
xi |
pi 1 |
|
i 1 |
|
|
n |
|
4- |
pi |
1 |
i 1
33. Среднеквадратическое значение косвенных измерений определяется по формуле
1-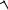 
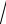D
2-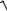 
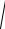M (x2 ) [M (x)]2
|
f |
2 |
2 |
|
f |
|
2 |
2 |
|
|
|
S x1 |
|
|
|
|
S x2 ... |
x |
x |
|
||||||
3- |
|
|
|
|
||||
|
1 |
|
|
|
|
2 |
|
|
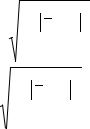
27
n
x xi 2
4- |
i 1 |
|
|
|
n 1 |
n
x xi 2
5- |
i 1 |
|
|
|
n |
34.Доверительному интервалу М соответствует доверительная вероятность
1.1
2.0,95
3.0,68
35.Площадь под кривой Гаусса, соответствующая интервалу
М 3 , равна |
|
|
1. 100% |
2. 95% |
3. 68% |
36. Условие нормировки для нормального распределения дискретных случайных величин выражается формулой
|
|
|
1- |
xf (x)dx 1 |
|
|
|
|
|
|
|
2- |
f (x)dx 1 |
|
|
|
|
|
n |
|
3- |
xi |
pi 1 |
|
i 1 |
|
|
n |
|
4- |
pi |
1 |
i1
37.Размерность среднеквадратического значения
1.отсутствует (Размерности нет)
2.соответствует размерности случайной величины
3.соответствует размерности квадрата случайной величины
38. Размерность дисперсии
1. отсутствует (Размерности нет)
2.соответствует размерности случайной величины
3.соответствует размерности квадрата случайной величины
39.Размерность математического ожидания
1.отсутствует (Размерности нет)
2.соответствует размерности случайной величины
3.соответствует размерности квадрата случайной величины
40.Размерность среднего арифметического значения
1.отсутствует (Размерности нет)
28
2.соответствует размерности случайной величины
3.соответствует размерности квадрата случайной величины