
Статистика учебное пособие 2012 иностр
.pdf1
СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ МЕДИКО-БИОЛОГИЧЕСКОЙ ИНФОРМАЦИИ
КРАТКАЯ ТЕОРИЯ
В медицине необходимо вести учет, анализ и прогноз различных массовых явлений. В целом, массовым явлениям присущи свои особые закономерности. К доктору обращаются пациенты с различными заболеваниями. Болезнь конкретного человека - случайное событие для врача. Но случайные события предсказуемы, например, в период эпидемии гриппа наиболее часто встречаются заболевания гриппом. Закономерности массовых случайных событий - статистических данных, отражающих эти события, - изучаются с помощью математической статистики. Математическая статистика использует основные понятия и положения теории вероятностей.
Типичная задача математической статистики - это приближенная оценка неизвестной вероятности случайного события по результатам наблюдений, экспериментов, когда событие может происходить или не осуществляться. Поэтому необходимо вычислять различные вероятности и сравнивать их между собой. Такие задачи необходимо решать специалистам по генетике, экологии, демографии, в различных областях медицины. Подробно практическое применение в медицине статистических методов рассматривается в курсе социальной гигиены и организации здравоохранения.
Случайной величиной называется переменная величина, значение которой зависит от исхода некоторого испытания.
Дискретной называется случайная величина, которая может принимать значения некоторой конечной или бесконечной числовой последовательности (число таблеток в упаковке, больных в палате, студентов в аудитории . . .).
Непрерывной называется случайная величина, которая может принимать любые значения внутри некоторого интервала (масса, температура, рост . . ).
Распределение дискретной случайной величины
Дискретная случайная величина считается заданной, если указаны ее возможные значения и соответствующие им вероятности:
Дискретные случайные |
х1 |
х2 |
х3 |
х4 |
х5 . . . . . |
величины Х i |
|
|
|
|
|
Вероятность Рi |
Р1 |
Р2 |
Р3 |
Р4 |
Р5 . . . . |
2
Совокупность Хi и Рi называется распределением дискретной случайной величины.
Поскольку все возможные значения дискретной случайной величины представляют полную систему, то сумма вероятностей равна 1:
n
P( xi ) 1 условие нормировки i 1
Различные распределения
1.Биномиальное распределение (позволяет определить вероятность того, что событие А произойдет раз при n испытаниях).
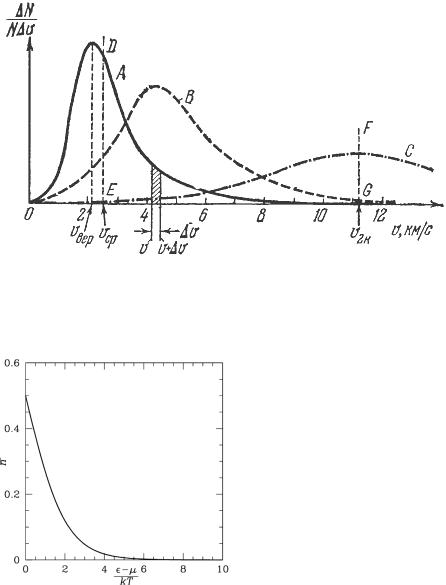
2.Распределение Максвелла (распределение газовых молекул по скоростям, кинетическим энергиям. График - кривая Максвелла).
На рисунке показано распределен ие молекул газа по скоростям - распределен ие Максвелла, которое
строго верно для газа, находящегося в покое
3. Распределение Больцмана (распределение частиц по потенциальным энергиям в силовых полях - гравитационном, электрическом.
График - экспонента).
Это распределение приемлемо к частицам, находящимся в состоянии хаотического теплового движения.
3
4.Нормальное распределение (график - кривая Гаусса).
5.Распределение Пуассона (вероятностная модель редких событий - эпидемии, космические лучи, аварии, распределение изюминок в булочке) и др.
Нормальный закон распределения имеет важное
практическое значение в естественных науках. Оказывается, распределение роста, массы новорожденных, параметров частоты сердечных сокращений, давления, жизненной ѐмкости лѐгких, частоты дыхания и много других случайных событий физической и биологической природы описываются нормальным законом распределения и графически иллюстрируется кривой Гаусса. Для понимания этого закона необходимо изучить терминологию и освоить новые понятия числовых характеристик дискретных и непрерывных случайных величин.
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Дискретные величины
Математическое ожидание (среднее значение) случайной величины есть сумма произведений всех возможных ее значений на вероятности этих значений:
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
М( Х ) х1 р1 х2 р2 .......хn pn xi pi |
|
|
|
|
|||||||
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
||
|
|
Среднее арифметическое значение |
|
|
|
|
|
|
|
|
|
|||
|
|
|
m1x1 m2x2 ....... mnxn |
|
m1 |
x |
|
m2 |
x |
..... |
mn |
x |
||
X |
||||||||||||||
|
|
|
|
|
||||||||||
|
|
|
n |
n |
1 |
|
n |
2 |
|
|
n |
n |
||
|
|
|
|
|
|
|
|
|
||||||
Обычно среднее арифметическое значение обозначается так: |
х ; <x>; |
|
||||||||||||
xср. |
|
|
|
|
|
|
|
|
|
|||||
|
m |
P, |
а |
|
М( х ) |
||
Если n велико, то относительная частота |
Х |
||||||
n |
|
||||||
|
|
|
|
||||
|
|
|
|
|
|||
Математическое ожидание часто отождествляют со средним арифметическим значением.
Дисперсия случайной величины - математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
4
D( x ) M x M( x ) 2 D( x ) M( x2 ) M( x ) 2
Дисперсия характеризует рассеяние случайных величин относительно математического ожидания. Размерность дисперсии - квадрат размерности случайной величины, поэтому введена величина

 D( x ) - среднеквадратическое отклонение, которое имеет размерность случайной величины.
D( x ) - среднеквадратическое отклонение, которое имеет размерность случайной величины.
Непрерывные случайные величины
dР - вероятность того, что непрерывная случайная х принимает значения между х и х + dx. Вероятность зависит от самой случайной величины и интервала dx.
dP = f(x)dx
где f(x) - плотность вероятности или функция распределения вероятностей. Она показывает, как изменяется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от значения самой
этой величины: f ( x ) dP |
|
|
dx |
в |
|
Paв f ( x ) dx |
-вероятность того, что случайная величина |
а
принимает значения в интервале (aв)
|
|
|
1 |
f ( x ) dx |
- условие нормировки для непрерывной |
|
|
|
случайной величины
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F( x ) |
f ( x ) dx - функция распределения непрерывной |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
случайной величины. |
|
|
|
|
|
|
||||||||||
Это вероятность того, что случайная величина принимает значения от |
|
||||||||||||||||||||||
―-― бесконечности до х. F( x ) |
P( |
|
|
X |
x ) |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Математическое ожидание: M( X ) |
x f ( x ) dx |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсия: |
|
|
D( X ) |
x M( X ) 2 f ( x ) dx |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x M( X ) 2 |
|
|||||
|
|
|
|
|
|
|
|
|
f ( x ) |
|
|
|
|
2 2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|||||||
Нормальный закон распределения: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
е = 2.71828. . . , е = ехр (экспонента), ех = ехр(х), |
|
е-х = ехр(-х) |
|
|
|||||||||||||||||||
График нормального закона - кривая Гаусса. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Иные записи закона Гаусса (нормального закона распределения): |
|
||||||||||||||||||||||
|
|
1 |
|
|
|
x M( x ) |
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
x M( x ) |
2 |
||
f ( x ) |
|
|
|
exp |
|
; f ( x ) |
|
|
|
|
|
|
exp |
|
|||||||||
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
2 D |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2D |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
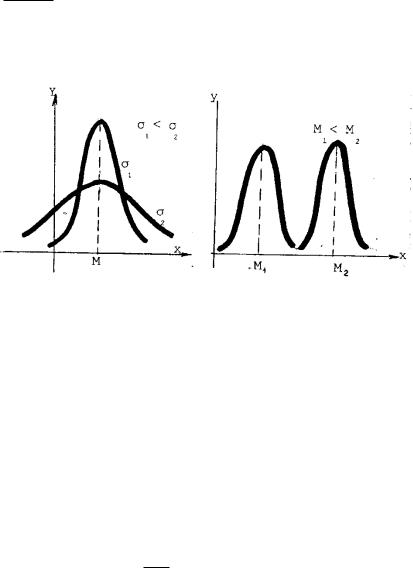
ОСОБЕННОСТИ КРИВОЙ ГАУССА:
- колоколообразная форма.
-ветви кривой Гаусса - экспоненты (убывающая и возрастающая)
- кривая Гаусса симметрична относительно х = М(х).
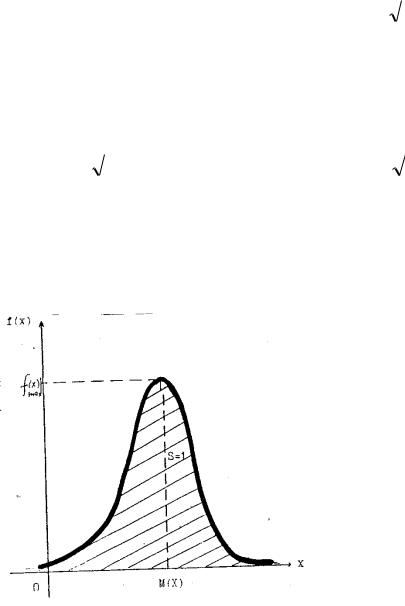
М(Х) является центром рассеивания; -максимум кривой Гаусса
соответствует точке с координатами (х, fмакс(х)),
6
х= М(х);
-координаты максимума кривой Гаусса определяем по формуле
нормального распределения, учитывая х = М(х):
fмакс( х ) |
|
1 |
|
|
|
|
|
|
|
|
|
(вершина графика); |
|
|
|
|
|
|
||
|
|
2 |
||||
|
|
|
||||
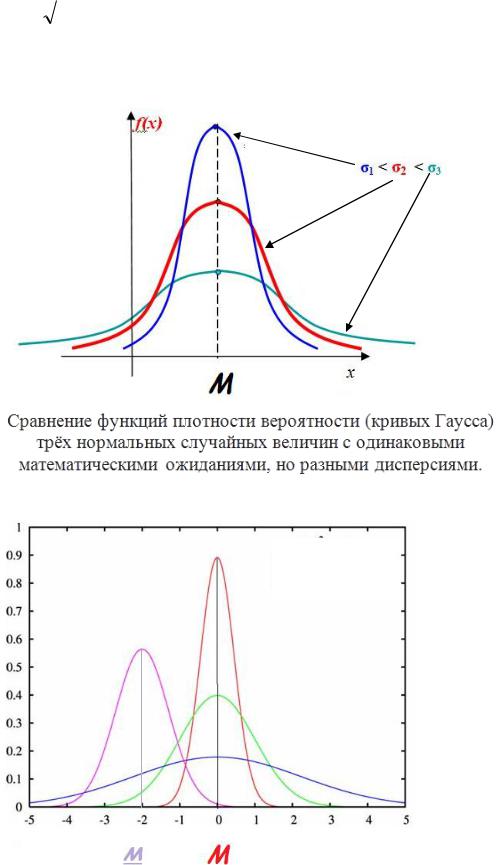
-ветви асимптотически приближаются к оси ОХ, |
||||||
чем больше |
, тем менее острая вершина, |
|||||
изменение математического ожидания М(х) сдвигает вершину графика влево или вправо,
7
площадь, заключенная под кривой равна 1 (выполняется условие нормировки);
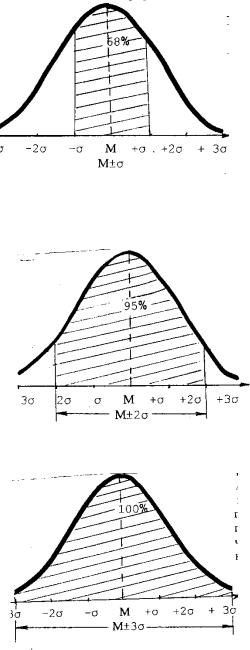
выполняется правило «трѐх сигм»;
нормальному распределению соответствует симметричная гистограмма.
Графическая иллюстрация правила «трѐх сигм»
1.Вероятность появления случайной величины в интервале значений ( М( Х ) ) равна 68%
То есть в интервале значений ( М( Х ) ) находится 68% случайных величин из
нормального распределения случайных величин.
2.Вероятность появления случайной величины в интервале значений М( Х ) 2 равна 95%
То есть в интервале значений ( М( Х ) 2 ) находится 95%
случайных величин из нормального распределения случайных величин.
3.Вероятность появления случайной величины в интервале значений ( М( Х ) 3 ) равна 100%- точнее 99,97%,
(это соответствует условию нормировки: площадь под кривой равна 1), следовательно. практически все случайные величины нормального распределения находятся под кривой Гаусса.
То есть в интервале значений ( М( Х ) 3 ) находится 100 % (точнее - 99,97%)
случайных величин из нормального распределения случайных величин.
8
Гистограмма
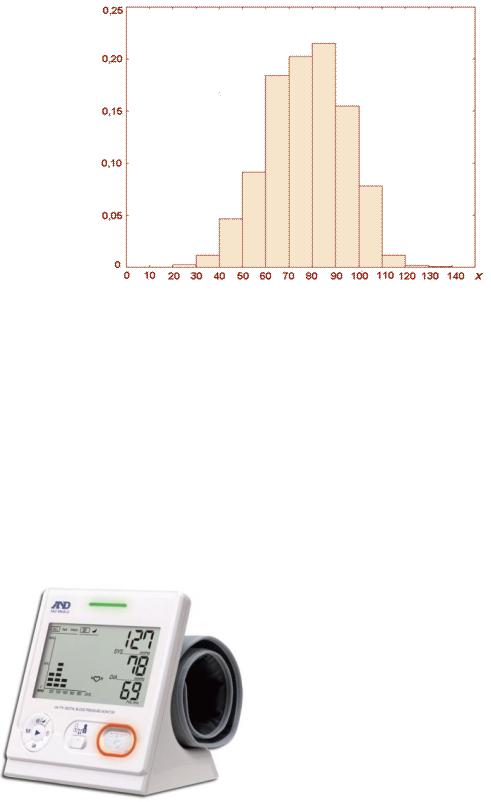
Гистограмма (от греч. histos, здесь столб + grámma — черта, буква, написание) — способ графического представления табличных данных. Гистограмма в виде столбиковой диаграммы используется в статистике для графического представления распределения вероятностей значений некоторой случайной величины.
Для нормального закона распределения характерен симметричный вид гистограммы.
По форме гистограммы можно оценить, какому статистическому закону распределения подчиняется случайная величина. Например, если все столбцы гистограммы примерно одинаковы, то равномерному, если в виде симметричного «холма», как представлено на рисунке, то нормальному закону распределения. По гистограмме на рисунке можно предположить, что случайная величина x описывается законом, близким к нормальному, и имеет наиболее вероятное значение, лежащее в пределах 80-90. Достаточно вероятными будут значения из интервала 60-100, и очень маловероятными – меньше 30 и больше 120.
Гистограмма частот - это совокупность |
смежных |
|
прямоугольников, построенных |
на |
|
одной прямой линии. Основания |
||
прямоугольников одинаковы, а высоты |
||
равны относительной |
частоте |
m/n |
(вероятности). |
|
|
Современный тонометр, |
|
|
используемый как домашний |
|
|
кардиоцентр, представляет не только результаты измерения артериального давления и пульса, но и построение
9
гистограмм, наглядных графиков результатов измерения.
Пакет анализа данных MS Excel позволяет построить из любого ряда данных гистограмму распределения значений,
автоматически
рассчитывая оптимальные параметры. На рисунке представлено графическое
распределение значений концентрации гемоглобина.
Чем большее число наблюдений будет в исследовании, тем лучше получится график функции с симметричным видом.
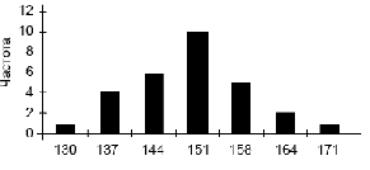
В качестве примера далее приведен фрагмент отчета по учебноисследовательской самостоятельной работе студентов - УИРС, по изучению распределений случайных величин антропометрических данных, таких как, ЖЕЛ (жизненная ѐмкость лѐгких),ЧСС (частота сердечных сокращений), рост, масса, АД (артериальное давление),ЧД (частота дыхания).
ЗАДАНИЕ: исследовать значение пульса студентов I курса.
ОТЧЕТ:
1. Учтены данные измерений частоты сердечных сокращений - ЧСС 50 студентов I курса.
2. Представляем полученные данные в виде статистического ряда:
74 |
84 |
86 |
79 |
77 |
74 |
64 |
87 |
80 |
83 |
90 |
55 |
60 |
60 |
74 |
74 |
68 |
72 |
63 |
65 |
66 |
65 |
69 |
63 |
78 |
80 |
86 |
82 |
79 |
79 |
68 |
87 |
87 |
87 |
78 |
65 |
65 |
70 |
79 |
78 |
73 |
73 |
68 |
74 |
70 |
70 |
70 |
83 |
78 |
94 |
3. Выделяем max и min значения ЧСС:
ЧССmin = 55 удар/мин ЧССmax= 94 удар/мин

10
4.При обработке статистических значений берѐм 5 интервалов с шириной интервала ЧСС
ЧСС = |
|
X max X min |
|
100 50 |
10 , В качестве Хmax |
взяли максимальный |
|
5 |
5 |
||||||
|
|
|
|
||||
десяток, |
в который |
входит |
ЧССmax, т.е. 100, а в |
качестве Хmin взяли |
|||
минимальный десяток, в который входит ЧССmin, т.е. 50.
Полученные интервалы: 50 – 60; 60 – 70; 70 – 80; 80 – 90; 90 – 100.
Середины интервалов соответственно равны: 55, 65, 75, 85, 95.
При расчѐте попадания случайных величин в каждый интервал нижний предел входит в данный интервал, а верхний не входит, так как он учитывается далее как нижний предел в следующем интервале. Например, значение 60 мы учитываем только во втором интервале. Значения 70, 80, 90 учитываем в следующих интервалах, которые они открывают.
5.В работе используются следующие формулы для определения числовых характеристик изучаемого распределения:
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
ЧСС |
|
|
ЧСС i М (ЧСС) |
|
|
|
|
||||
а) f(ЧСС1 ) = |
|
|
|
exp |
|
|
|
|
|
; f(ЧСС i )- плотность |
||||
|
|
|
|
|
2 |
2 |
||||||||
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вероятности.
Функция кривой Гаусса для расчета значений по отношению к середине интервала (ЧССi);
б) |
fmax |
= |
ЧСС |
- |
|
максимальное значение кривой |
Гаусса (для |
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
математического ожидания); |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
ЧСС1 ЧСС2 |
...ЧСС50 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
в) |
ЧСС |
- |
среднее арифметическое значение |
|||||||||||||||||||||||||
|
|
|
|
|
|
50 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
частоты сердечных сокращений; |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
г) М(ЧСС) |
|
|
= ЧCC1 p1 ЧCC 2 |
p2 ЧCC 3 p3 ЧCC 4 p4 |
ЧCC 5 p5 - |
|||||||||||||||||||||||
математическое ожидание ( P |
mi |
); |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
ni |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
5 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
д) D = [ |
ЧСС |
i |
М (ЧСС)] pi - дисперсия; |
|
|
|
||||||||||||||||||||||
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
е) |
|
|
|
|
|
|||||||||||||||||||||||
D - среднеквадратическое отклонение. |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисляем эти параметры. |
|
|
|
||||||||||
