Статистические методы обработки медико-биологической информации
КРАТКАЯ ТЕОРИЯ
В медицине необходимо вести учет, анализ и прогноз различных массовых явлений. В целом, массовым явлениям присущи свои особые закономерности. К доктору обращаются пациенты с различными заболеваниями. Болезнь конкретного человека - случайное событие для врача. Но случайные события предсказуемы, например, в период эпидемии гриппа наиболее часто встречаются заболевания гриппом. Закономерности массовых случайных событий - статистических данных, отражающих эти события, - изучаются с помощью математической статистики. Математическая статистика использует основные понятия и положения теории вероятностей.
Типичная задача математической статистики - это приближенная оценка неизвестной вероятности случайного события по результатам наблюдений, экспериментов, когда событие может происходить или не осуществляться. Поэтому необходимо вычислять различные вероятности и сравнивать их между собой. Такие задачи необходимо решать специалистам по генетике, экологии, демографии, в различных областях медицины. Подробно практическое применение в медицине статистических методов рассматривается в курсе социальной гигиены и организации здравоохранения.
Случайной величиной называется переменная величина, значение которой зависит от исхода некоторого испытания.
Дискретной называется случайная величина, которая может принимать значения некоторой конечной или бесконечной числовой последовательности (число таблеток в упаковке, больных в палате, студентов в аудитории ...).
Непрерывной называется случайная величина, которая может принимать любые значения внутри некоторого интервала (масса, температура, рост ..).
Распределение дискретной случайной величины
Дискретная случайная величина считается заданной, если указаны ее возможные значения и соответствующие им вероятности:
|
Дискретные случайные величины X j |
Xi |
Х2 |
Хз |
х4 |
Х5 |
|
Вероятность Р; |
Pi |
р2 |
Рз |
р4 |
р5 .... |
Совокупность X, и Pj называется распределением дискретной случайной величины.
Поскольку всс возможные значения дискретной случайной величины представляют полную систему, то сумма вероятностей равна 1:
п
i=l
условие нормировки
Различные распределения
Биномиальное распределение (позволяет определить вероятность того, что событие А произойдет i раз при п испытаниях).
Распределение Максвелла (распределение газовых молекул по скоростям, кинетическим энергиям. График - кривая Максвелла).
Н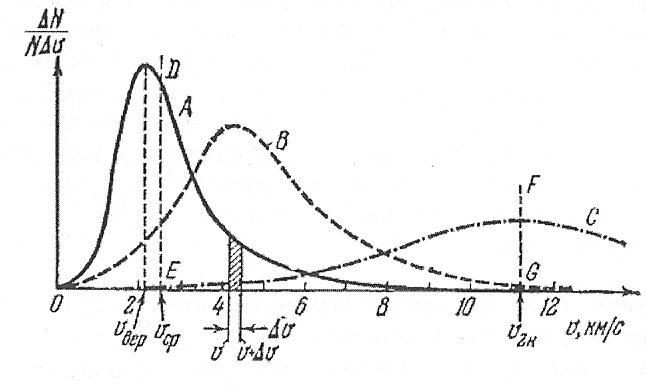
а
рисунке показано распределение молекул
газа по скоростям- распределение
Максвелла, которое строго верно для
газа, находящегося в покое
Распределение Больцмана (распределение частиц по потенциальным
э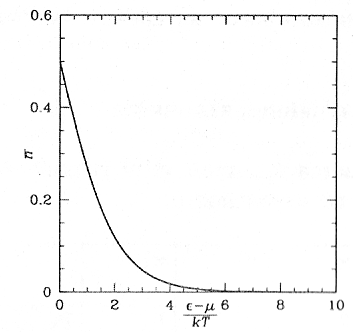
нергиям
в силовых полях
гравитационном, электрическом. График - экспонента).
Это распределение приемлемо к частицам, находящимся в состоянии хаотического теплового движения.
Нормальное распределение (график - кривая Гаусса).
Распределение Пуассона (вероятностная модель редких событий - эпидемии, космические лучи, аварии, распределение изюминок в булочке) и др.
Нормальный закон распределения имеет важное практическое значение в естественных науках. Оказывается, распределение роста, массы новорожденных, параметров частоты сердечных сокращений, давления, жизненной ёмкости лёгких, частоты дыхания и много других случайных событий физической и биологической природы описываются нормальным законом распределения и графически иллюстрируется кривой Гаусса. Для понимания этого закона необходимо изучить терминологию и освоить новые понятия числовых характеристик дискретных и непрерывных случайных величин.