
- •Методическое пособие для студентов с примерами и задачами
- •Методическое пособие для студентов с примерами и задачами
- •Часть I
- •Часть 1
- •5. Если
- •Решение:
- •Решение:
- •V - скорость.
- •Решение
- •Решение
- •В медицине и биологии, например, используя производную, можноопределить быстроту изменения различных параметров системы илипроцесса в живом организме.
- •2. Вычисляем предел
- •3. Если предел существует и равен а, то
- •Решение:
- •4. Постоянный множитель можно выносить за знак неопределенного интеграла.
- •Свойства определенного интеграла:
- •2. Найти площадь фигуры, заключенной между
- •Тренинг: решение примеров
- •Часть III
- •2) Пусть, например, груз р массы m подвешен к пружине и находится вположении равновесия. Отклоняя его от положения равновесия с помощью
- •Дифференциальные уравнения высших порядков и системыдифференциальных уравнений.
- •Приложение
- •4.Корень от частного равен частному от деления корня из делимого накорень из делителя (показатели корней должны быть одинаковыми):
- •5.Чтобы возвести корень в степень, достаточно возвести в эту степеньподкоренное значение:
- •Формулы сложения:
- •Интегралы, содержащие только cos
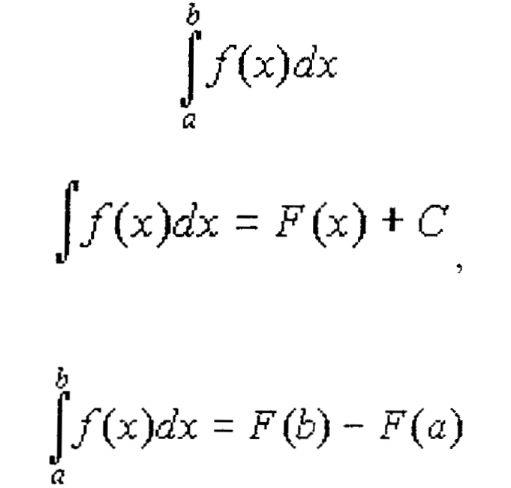
![]()
Свойства определенного интеграла:
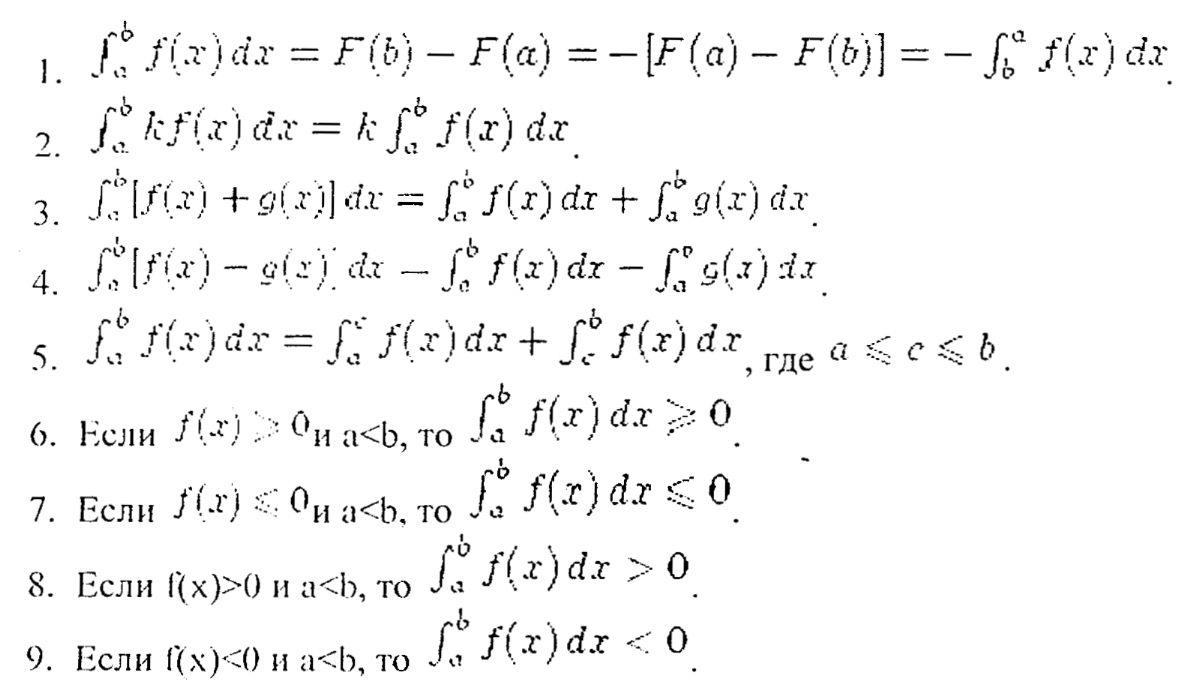
![]()
Определение. Приращение первообразных функций F(x)+C при переходеаргумента х от значения х=а к значению х=b, равное разности F(b)-F(a),называется определенным интегралом и обозначается символом
так, что если
то
Данное равенство называется формулой Ньютона - Лейбница,предполагается при этом, что подинтегральная функция f(x) непрерывна при всехзначениях х, удовлетворяющих условиям
Для вычисления определенных интегралов мы, как и отмечалось выше, будемрассматривать наиболее часто используемые методы - замену переменной и
![]()
Таким образом, искомый интеграл равен 6.
Геометрический смысл определенного интеграла
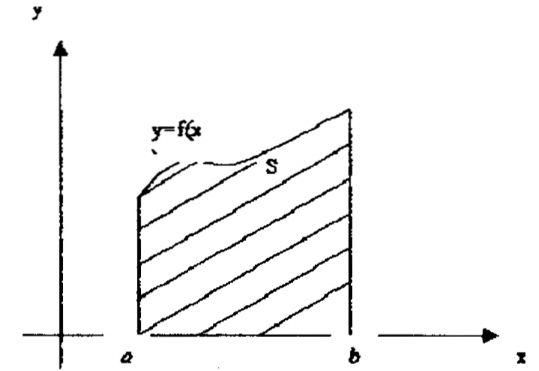
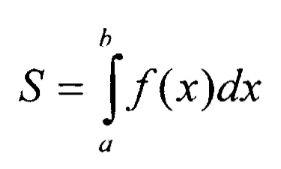
Примеры
интегрирование
по частям.Пример:
необходимо найти определенный интеграл
Решение:
1.
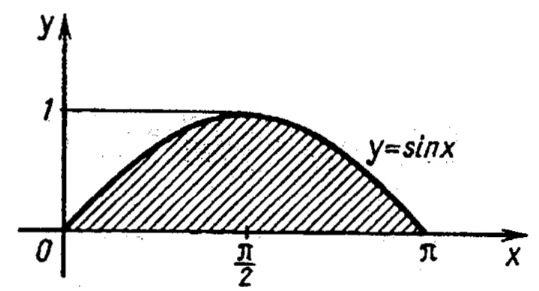
Найти площадь одной арки синусоиды.![]()
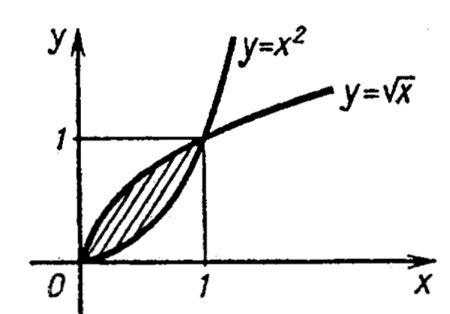
2. Найти площадь фигуры, заключенной между
Данная фигура ограничена графиками двухфункций:
дугами
парабол
![]()
![]()
![]()
:
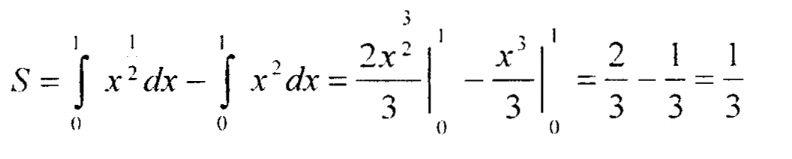
Вычисление объёмов тел с помощью интеграла
![]()
Пример.
Пусть Т— тело вращения, образованное вра-щением криволинейной трапеции вокруг осиабсцисс. Найти объем тела Т.Решение.
тогда
где
S
(х)
— площадь сечения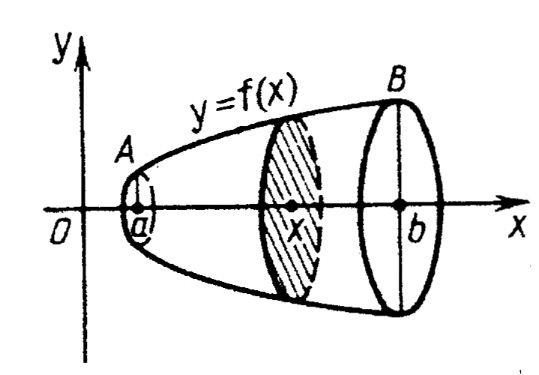
![]()
.
f(x),
значит,
Но
тогда![]()
Иногда![]()
пишут
так:
![]()
Приведенные ниже примеры демонстрируют наиболее типичныеслучаи нахождения определенного интеграла.
Пример №1. Нахождение определенного интеграла с помощью формулы Ньютона- Лейбница
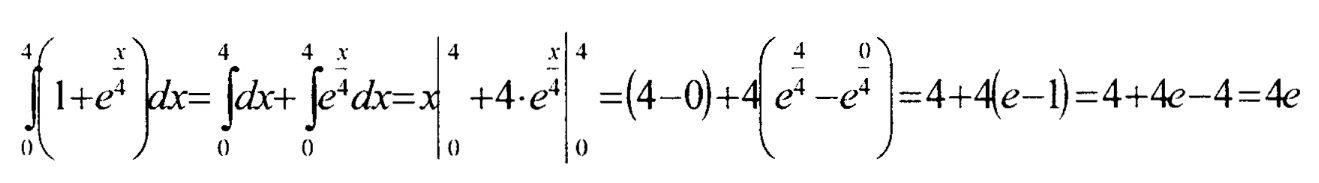
Пример №2. Нахождение определенного интеграла методом замены переменнойинтегрировани
я
Введем
новую переменную интегрирования:
Заменим
пределы интегрирования относительно
новой переменной t:
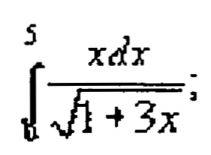
![]()
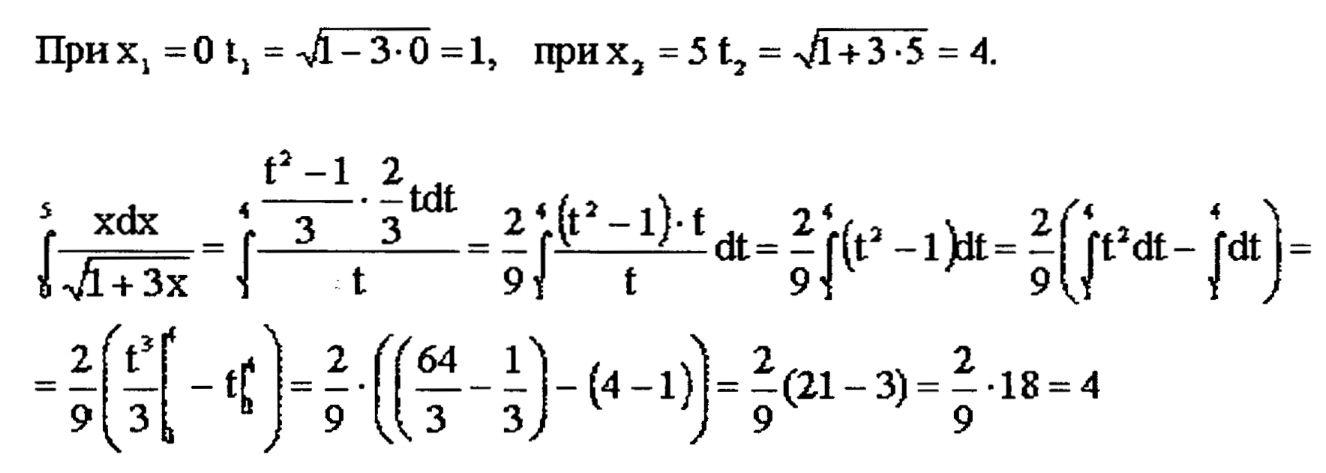
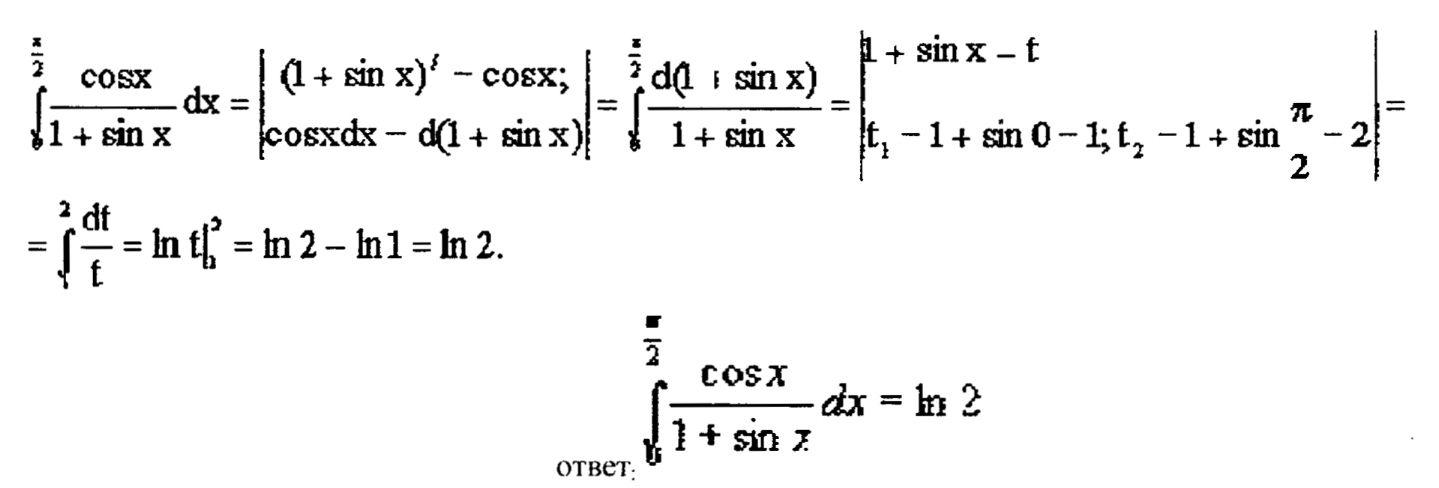
ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ
• Соотношения между перемещением S и скоростью v:
![]()
Так как скорость характеризует быстроту процесса, то, зная, к примеру, скорость ростаклеток, размножения бактерий, радиоактивного распада, ...можно определит
ь
соответствующие зависимости от времени количества образующихся клеток, бактерий,распавшегося вещества и т.д., используя метод интегрирования.
![]()
![]()
![]()
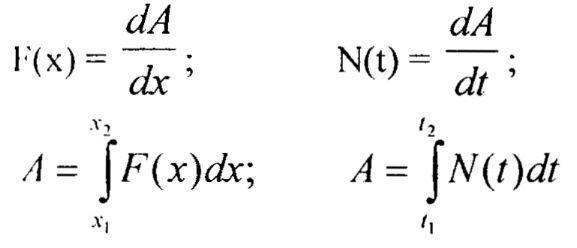
Соотношения между массой m и плотностью р:
Соотношения между электрическим зарядом q и силой тока I:
Соотношения между теплоёмкостью с и количеством теплоты Q:
![]()
