
- •Методическое пособие для студентов с примерами и задачами
- •Методическое пособие для студентов с примерами и задачами
- •Часть I
- •Часть 1
- •5. Если
- •Решение:
- •Решение:
- •V - скорость.
- •Решение
- •Решение
- •В медицине и биологии, например, используя производную, можноопределить быстроту изменения различных параметров системы илипроцесса в живом организме.
- •2. Вычисляем предел
- •3. Если предел существует и равен а, то
- •Решение:
- •4. Постоянный множитель можно выносить за знак неопределенного интеграла.
- •Свойства определенного интеграла:
- •2. Найти площадь фигуры, заключенной между
- •Тренинг: решение примеров
- •Часть III
- •2) Пусть, например, груз р массы m подвешен к пружине и находится вположении равновесия. Отклоняя его от положения равновесия с помощью
- •Дифференциальные уравнения высших порядков и системыдифференциальных уравнений.
- •Приложение
- •4.Корень от частного равен частному от деления корня из делимого накорень из делителя (показатели корней должны быть одинаковыми):
- •5.Чтобы возвести корень в степень, достаточно возвести в эту степеньподкоренное значение:
- •Формулы сложения:
- •Интегралы, содержащие только cos
4. Постоянный множитель можно выносить за знак неопределенного интеграла.
Таблица первообразных
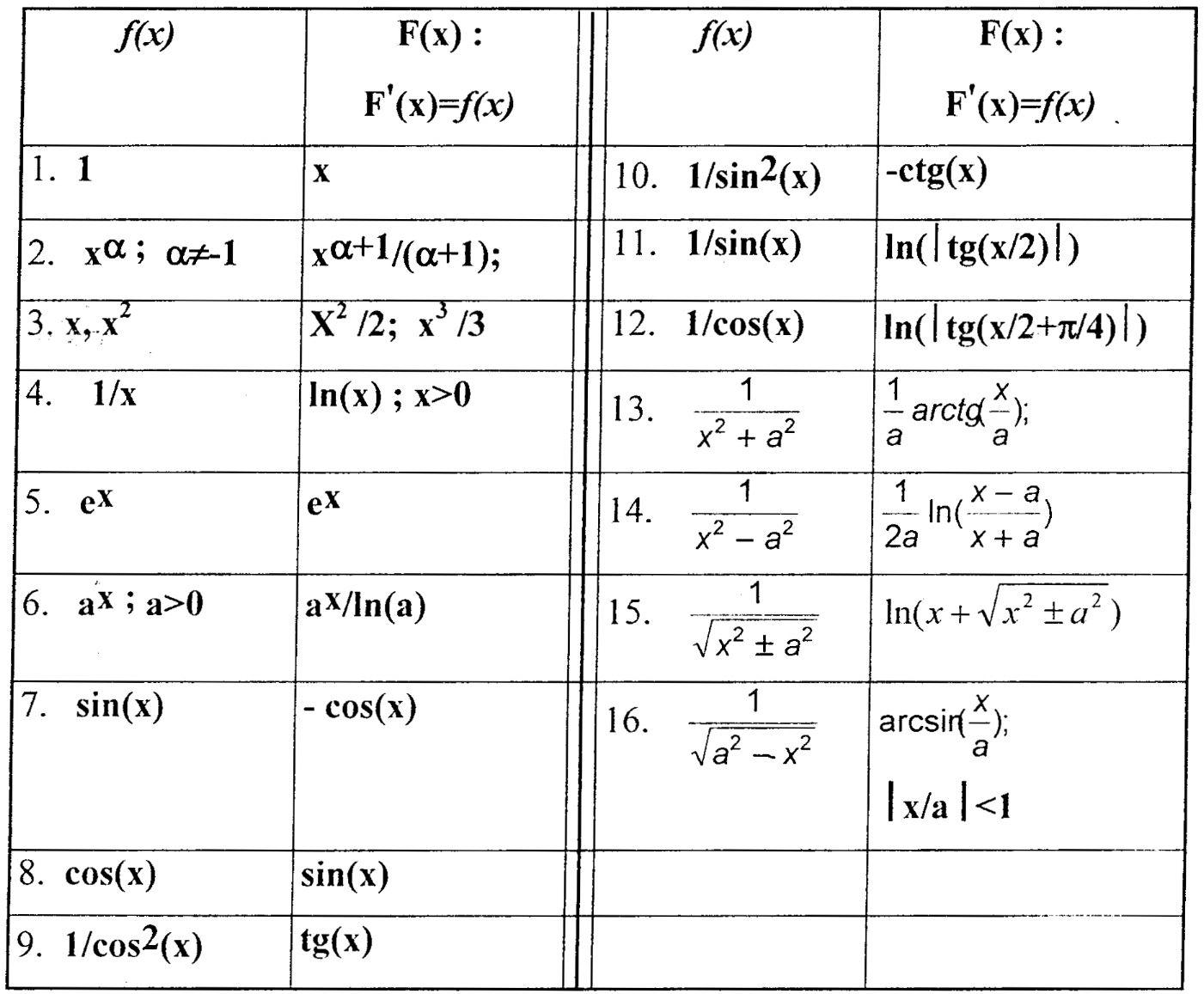
Таблица
неопределённых интегралов

Используя свойства неопределенных интегралов и таблицу основных интегралов,можно интегрировать некоторые функции.
Пример.
![]()
Пример.
Пример.
Правил для интегрирования произведения, частного, сложной, обратной функции вобщем случае нет. Рассмотрим отдельные приёмы интегрирования некоторыхклассов функции.
![]()
Наиболее общим приёмом интегрирования функций является методподстановки, который применяется тогда, когда искомый интегралявляется табличным, но путем ряда элементарных преобразований он может бытьсведен к табличному.
![]()
![]()
![]()
где x=φ(t) - дифференцируемая функция от t, производная которой φ'(t) сохраняетзнак для рассматриваемых значений переменных.Сущность применения этой формулы состоит в том, что в данном интеграле
![]()
переменную .т заменяют переменной / по формуле х=φ(t) и,следовательно, dx произведением φ'(t)dt.
Продифференцировав
правую часть формулы, имеем
![]()
![]()
Таким образом, формула справедлива.
Часто употребляется обратная замена переменной, т.е. подстановка t=φ'(x).
dt=φ'(x)dx
Пример: Необходимо найти интегра
л
![]()
Подставляя
полученные значения в искомый интеграл
получим:
![]()
Теперь
подставив значение
и
в полученное выражение получим
решениеискомого
интеграла:
![]()
С = 0.
Интегрирование по частям
![]()
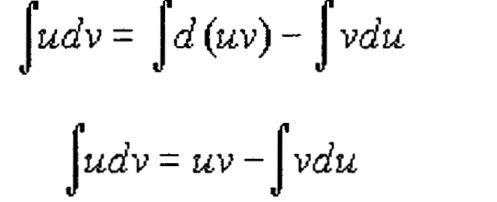
Отсюда
Интегрируя обе части этого равенства, имеем
или
Интегрированием по частям называется интегрирование с помощью полученнойформулы.
Основные случаи, когда применяется данный способ интегрирования:
подинтегральная функция содержит произведение многочлена от х напоказательную функцию от х или произведение многочлена от х на sin(x) илиcos(x), или произведение многочлена от х на 1п(х)\
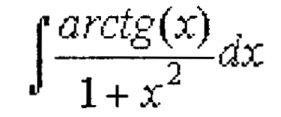
Применим подстановку: u=arctg(x), тогда
подинтегральная функция представляет собой одну из обратныхтригонометрических функций arcsin(x), arcos(x) и т.д.;подинтегральная функция есть произведение показательной функции на sin(x)или cos(x).
![]()
Пример: необходимо найти интегра
л
Положим
и = х,
dv
=
sin(x)dx.Тогда
du
=
dx,
v
=
-cos(x).
Отсюда
![]()
Пример: вычислить интегралПредставим удобную запись вычислений:
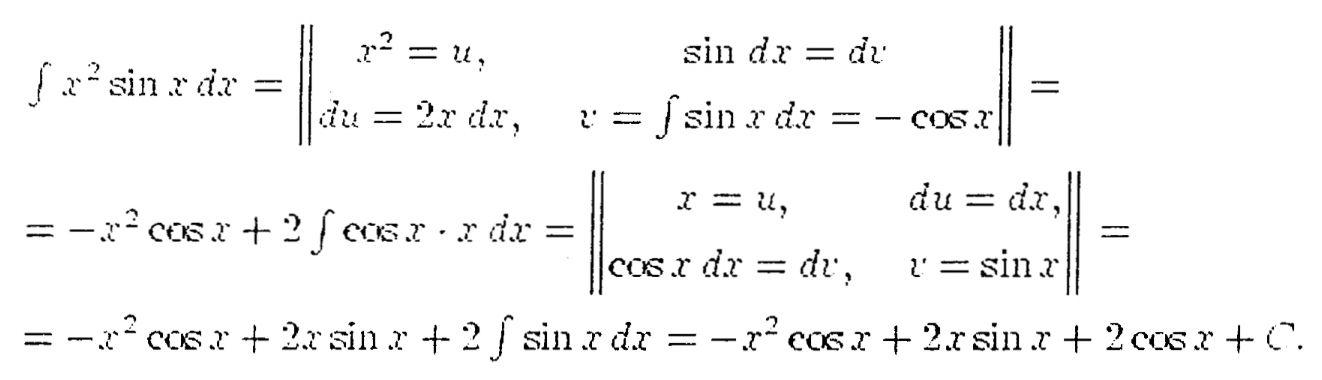
Здесь в двойные вертикальные линии заключены все вычисления, которыеявляются подготовительными для применения формулы интегрирования почастям. Подготовительные записи могут быть вынесены за пределы уравнения.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Задача. Найти приращение функции, первообразной для функции f(x), припереходе аргумента х от значения а к значению b.Решение. Положим, что интегрированием найдено
![]()
Тогда F(x)+C1, где С1 - любое данное число, будет одной из первообразныхфункций для данной функции f(x). Найдем её приращение при переходе аргументаот значения а к значению b. Получим:
![]()
Как видим, в выражении приращения первообразной функции F(x) + С1отсутствует постоянная величина С1. А так как под С1 подразумевалось любоеданное число, то полученный результат приводит к следующему заключению: припереходе аргумента х от значения х=а к значению х=b все функции F(x) + С,первообразные для данной функции f(x), имеют одно и то же приращение, равноеF(b)-F(a).
