2. Вычисляем предел
если
предел не
3. Если предел существует и равен а, то
существует,
то
не
существует.
Задача 2. Определить по известной функции f(х)
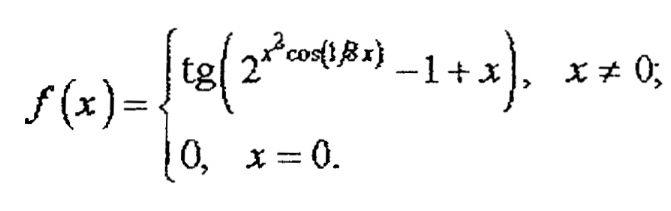
решение
Исходя
из определения производной, имеем:
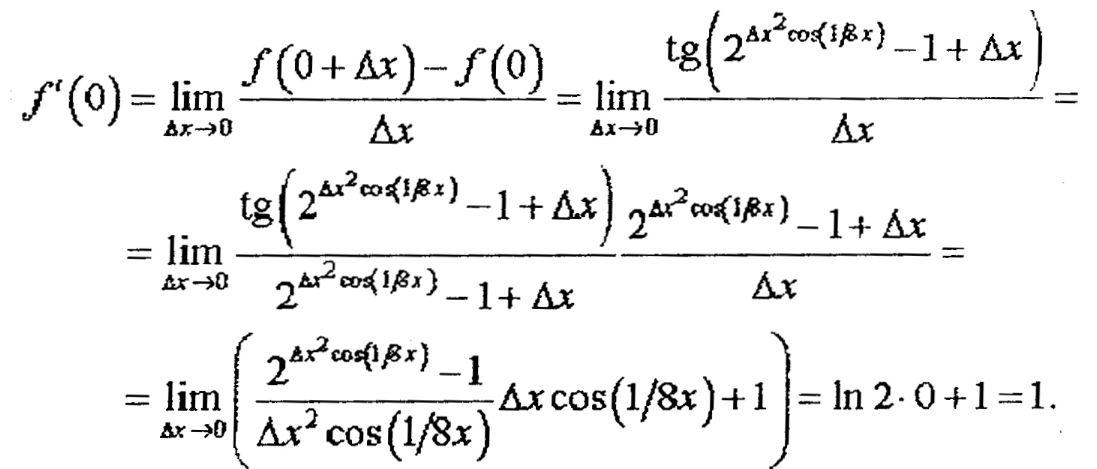
Отметим,
что хотя
при
не
определен, этот параметр является
конечной величиной. Т.е. заданная функция в точке х = 0 имеет производную
равную
единице:
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНО
Й
кривой
Пусть
в точке
существует
касательная к данной
кривой
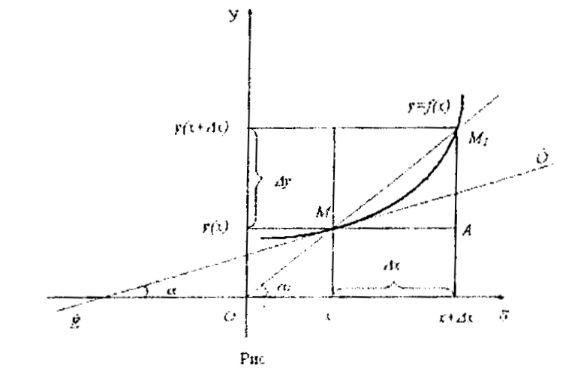
(рис.). Дадим аргументу х
приращение Δх и отметим па кривой точку
Проведем
секущую ММ1
и обозначим через
ɑ1
величину
угла, образованного секущей сположительным
направлением оси ОХ.
следует,
что отношение
Из
треугольника
(прямоугольного)
Если
точка
M1
будет
перемещаться вдолькривой,
приближаясь к точке М, то приэтом
секущая ММ1
и величина
ɑ1меняются
с изменением х. Предельным
положением секущей будет прямая, касательная к кривой в точке М,образующая с положительным направлением оси ОХ некоторый угол,величину которого обозначим через α.
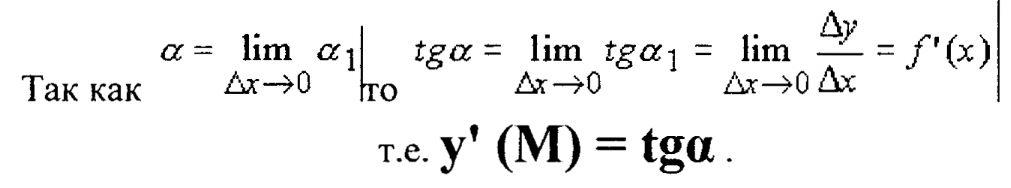
где
Если
Если
/или
нормали.
в
(1) и/или (2),
3.
Подставляя найденные значенияполучаем
уравнения касательной и
Пользуясь геометрическим смыслом производной, решим следующиезадачи:
в
Задача/. Составить уравнение касательной и/или нормали к кривойточке с абсциссой х0.
решение
Если
функция f(x)
в
точке х0
имеет конечную производную, тоуравнение
касательной имеет вид
,
то уравнение касательной имеет видто
уравнение нормали имеет вид
•
Если
то
уравнение нормали имеет вид
1.
Находим значение
2.
Находим производную
в
точке M1
с
абсциссой
Задача
3:
Найти уравнение касательной к параболе
решение
Будем
искать уравнение касательной в виде
уравнения прямой с угловымкоэффициентом,
т.е.
у = kx
+
b.
Известно, что к есть тангенс угла
наклонапрямой
к положительному направлению оси ОХ,
т.е. k
= у'(М1).Так
как М1
принадлежит и касательной и параболе,
то ее координатыудовлетворяют
их уравнениям.
решение
Уравнение
нормали:
Имеем:
•
Получаем
уравнение нормали:
• Составляем уравнение касательной к данной кривой в точке сабсциссой х0).
Уравнение
касательной:
Имеем:
•
Получаем
уравнение касательной:
В
точке М1
Подставив
x1
=
2 в уравнение параболы, найдем ординату
у1
точки М1:
Значит
М(2,9).
Найдем
x1=
2; y1
=
9 в уравнение прямой, найдем b:
9 = 8 • 2 + b;
b =
- 7.Значит
касательная к параболе у = Зх2
- 4х + 5 в точке
М1
(2,9)
будетпредставлена
уравнением
у = 8х — 7.
может
быть представлено в
то
соответствующее приращению аргумента
виде
где
A
не зависит от
но
то
функция
зависит
от
называется
дифференцируемой в точке х.
Здесь
бесконечно
малая более высокого порядка малости,
чем
т.е.
Можно
доказать, что
Таким
образом, существование
в
точке х
эквивалентно её
дифференцируемости в этой точке по определению 3.
Определение 4. Главная линейная часть приращения дифференцируемой
функции
называется
ее дифференциалом.
ДИФФЕРЕНЦИАЛ ФУНКЦИИ И ДИФФЕРЕНЦИАЛАРГУМЕНТ
А
ДИФФЕРЕНЦИАЛ
Рассмотрев
функцию
,
убедимся, что
является
функцией двух аргументов -
(дифференциал
независимой переменной совпадает с ее приращением). Дифференциалыстарших порядков определяются индуктивно.
и
по определению предела
По определению производнойполучим
:
или
где Δх при х = 0 тоже БМВ.Лейбниц предложил обозначить
и
назвать это дифференциалом функции.
Тогда, если у = х, то
Откуда
дифференциал аргумента dx
равен
приращению аргумента —Δх.
Можно (4) представить в виде:
• Пример.
Найти дифференциал функции
Решение: По формуле (6) получим:
Отсюда формулами для нахождения дифференциала будут формулыдля нахождения производной, где вместо знака производной передфункцией будет стоять символ d.
Например:
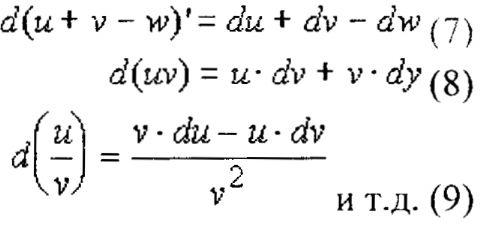
считается
функцией только х
(но не
),
т.е.
этом
Соотношение
выполняется,
например, для
n-1=1.
Методом
индукции из этого следует справедливость
аналогичноговыражения
для
n-го
дифференциала при любом n
≥
2 .
называется дифференциал от (n-1)-го дифференциала этой функции. При
• Пример. Вычислить 1-й и 2-й дифференциалы функции
