
- •Методическое пособие для студентов с примерами и задачами
- •Методическое пособие для студентов с примерами и задачами
- •Часть I
- •Часть 1
- •5. Если
- •Решение:
- •Решение:
- •V - скорость.
- •Решение
- •Решение
- •В медицине и биологии, например, используя производную, можноопределить быстроту изменения различных параметров системы илипроцесса в живом организме.
- •2. Вычисляем предел
- •3. Если предел существует и равен а, то
- •Решение:
- •4. Постоянный множитель можно выносить за знак неопределенного интеграла.
- •Свойства определенного интеграла:
- •2. Найти площадь фигуры, заключенной между
- •Тренинг: решение примеров
- •Часть III
- •2) Пусть, например, груз р массы m подвешен к пружине и находится вположении равновесия. Отклоняя его от положения равновесия с помощью
- •Дифференциальные уравнения высших порядков и системыдифференциальных уравнений.
- •Приложение
- •4.Корень от частного равен частному от деления корня из делимого накорень из делителя (показатели корней должны быть одинаковыми):
- •5.Чтобы возвести корень в степень, достаточно возвести в эту степеньподкоренное значение:
- •Формулы сложения:
- •Интегралы, содержащие только cos
Решение:
![]()
Пример
№2.
Вычислить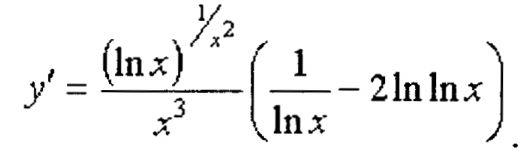
Решение:![]()
если
Старшие
производные функции одной переменной
имеет
индуктивный
Определение
производной n
-го порядка функции
![]()
![]()
![]()
называется
функции
Определение
2.
Производной порядка![]()
![]()
Таким
образом,
производная
определяется и вычисляется через
ю,та
— через
-ю,
и т.д.
порядка
функции
•
Пример.
Вычислить производную![]()
![]()
![]()
![]()
![]()
![]()
![]()
Решение:
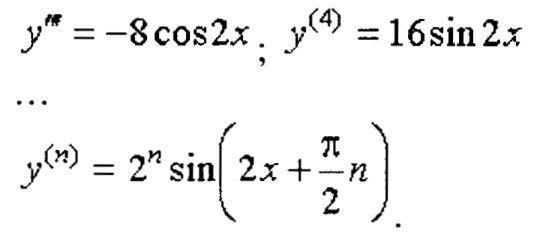
Последняя формула является предположением, основанным на предыдущемутверждении. Для n = 1,2,3,4 она выполняется. Предположим, что"угаданная" формула для производной (n-1) -го порядка верна. Покажем
,
по x:
Примененный
способ доказательства называется
методом полнойматематической
индукции.
Впрочем, по индукции можно доказать
формулу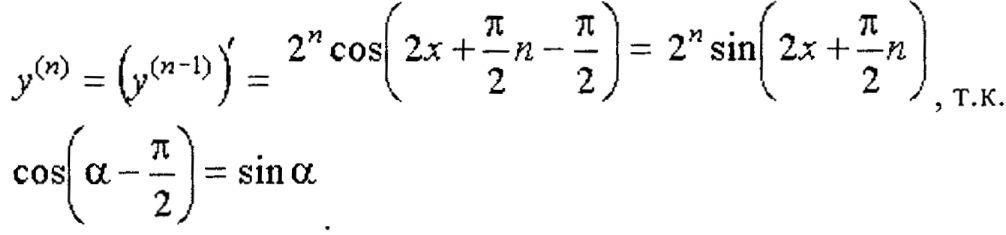
,
а затем, применив ее и формулу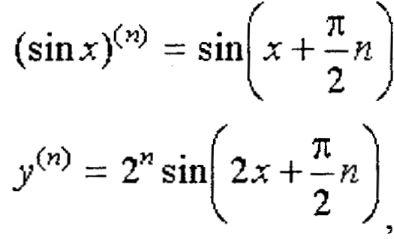
• Пример. Посчитаем 2-ю производную из примера № 1,
получить
выражение для
что
тогда она верна и для n-й
производной. Пусть
Продифференцируем
последнее равенство![]()
![]()
Решение:![]()
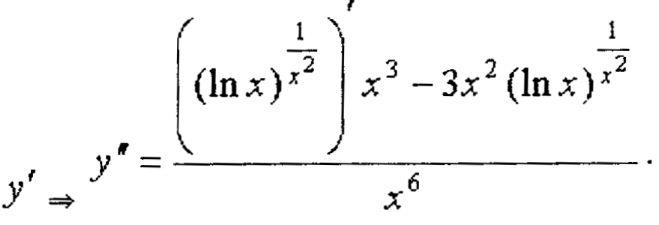
Продифференцируем
При
вычислении
использовалась
уже найденная в примере № 1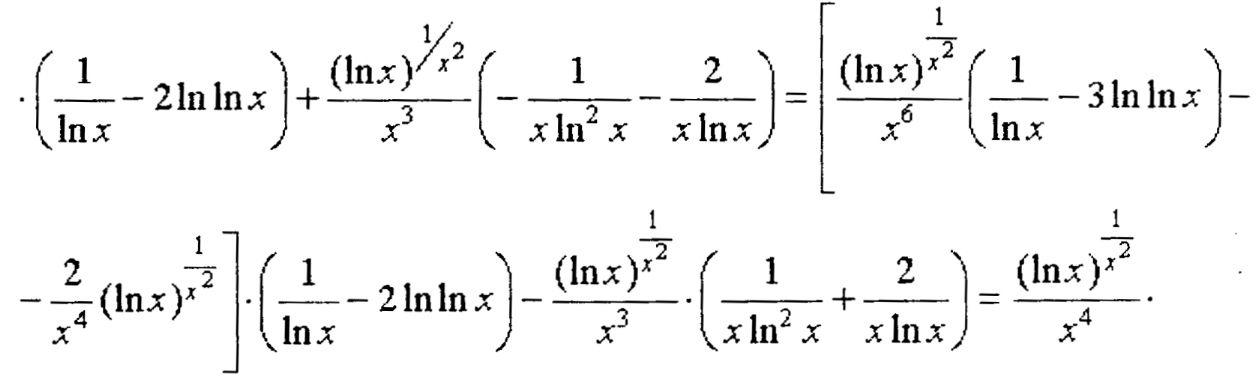
![]()
![]()
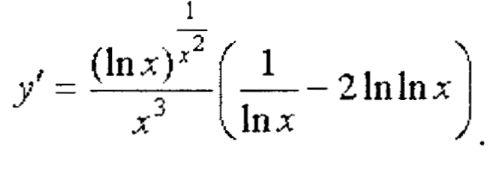
Механический смысл производной
Производная функции у=f(x) в точке x0 выражает скоростьизменения функции в точке x0 , то есть скорость протеканияпроцесса, описанного зависимостью у=f(x)
.
V - скорость.
Пусть
закон
прямолинейного движения. Тогда
выражает
мгновенную скорость движения в момент
времени![]()
![]()
![]()
![]()
Первая
производная от пути по времени, т.е.
![]()
а - ускорение
Вторая
производная
выражает
мгновенное ускорение в момент![]()
времени![]()
(вторая
производная от пути по![]()
Первая производная от скорости по времен
ивремени),
т.е.ускорение
где
обозначения
производных по времени, введенные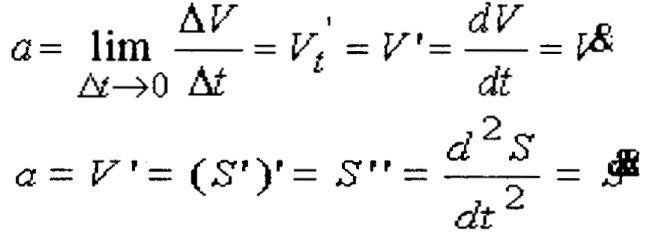
![]()
И.Ньютоном. Он впервые сформулировал, что с позиции механикимгновенная скорость прямолинейно движущейся точки есть перваяпроизводная от пути по времени, а её мгновенное ускорение естьпервая производная от скорости по времени или вторая производная отпути по времени.
т.е.
на 2-й секунде бега спринтер имеет
скорость 2,5 м/с.Решение
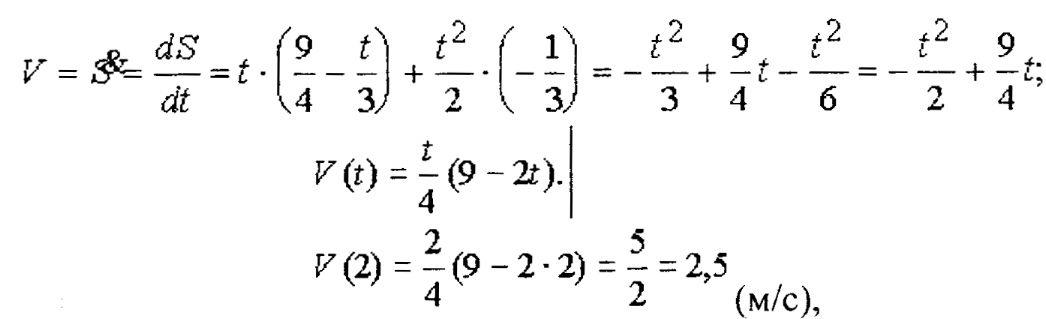
•
Пример.
Найти скорость спринтера через 2 с
после старта, если
его
путь изменяется по формуле:![]()
т.е.
в начале бега спринтер имел ускорение
2,25 м/с2Решение
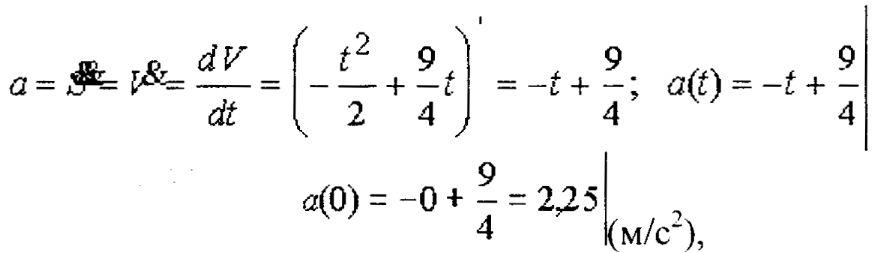
В медицине и биологии, например, используя производную, можноопределить быстроту изменения различных параметров системы илипроцесса в живом организме.
• Пример. При воздействии внешней среды давление наповерхность тела с течением времени меняется по закону
мм.рт.ст.![]()
Определите с какой скоростью изменяется давление на 10 секунде от началапроцесса.
решение
В
момент времени t
=
10 с![]()
Ответ:
В момент времени t
= 10 с давление изменяется со скоростью
59мм.рт.ст.
в секунду.
![]()
• В качестве примера можно рассмотреть понятие градиента.На рисунке представлено распределение скоростей разных слоевжидкости 1-5 при движении вязкой жидкости между двумяпластинами, из которых нижняя неподвижна, а верхняя движется соскоростью VB.
Слой у основания неподвижен. По мере приближения кверхней пластинке скорость слоев возрастает истремится к VB. При характеристике возникающих силтрения между слоями используется важный показательdV
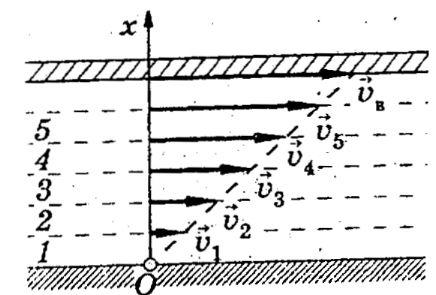
скорости на некотором участке в направлении х,
перпендикулярном скорости, отнесённое к длине этого участка. Величина
![]()
называется градиентом скорости или скоростью сдвига. В медицине,
при рассмотрении движения крови по сосудам и анализе вязкости крови
,
оценивают
значение скорости сдвига![]()
Задача 1: Исходя из определения производной, определите производнуюфункции f(х) в точке х = 0.
решение
1. По определению производной
![]()
,
но![]()
![]()
