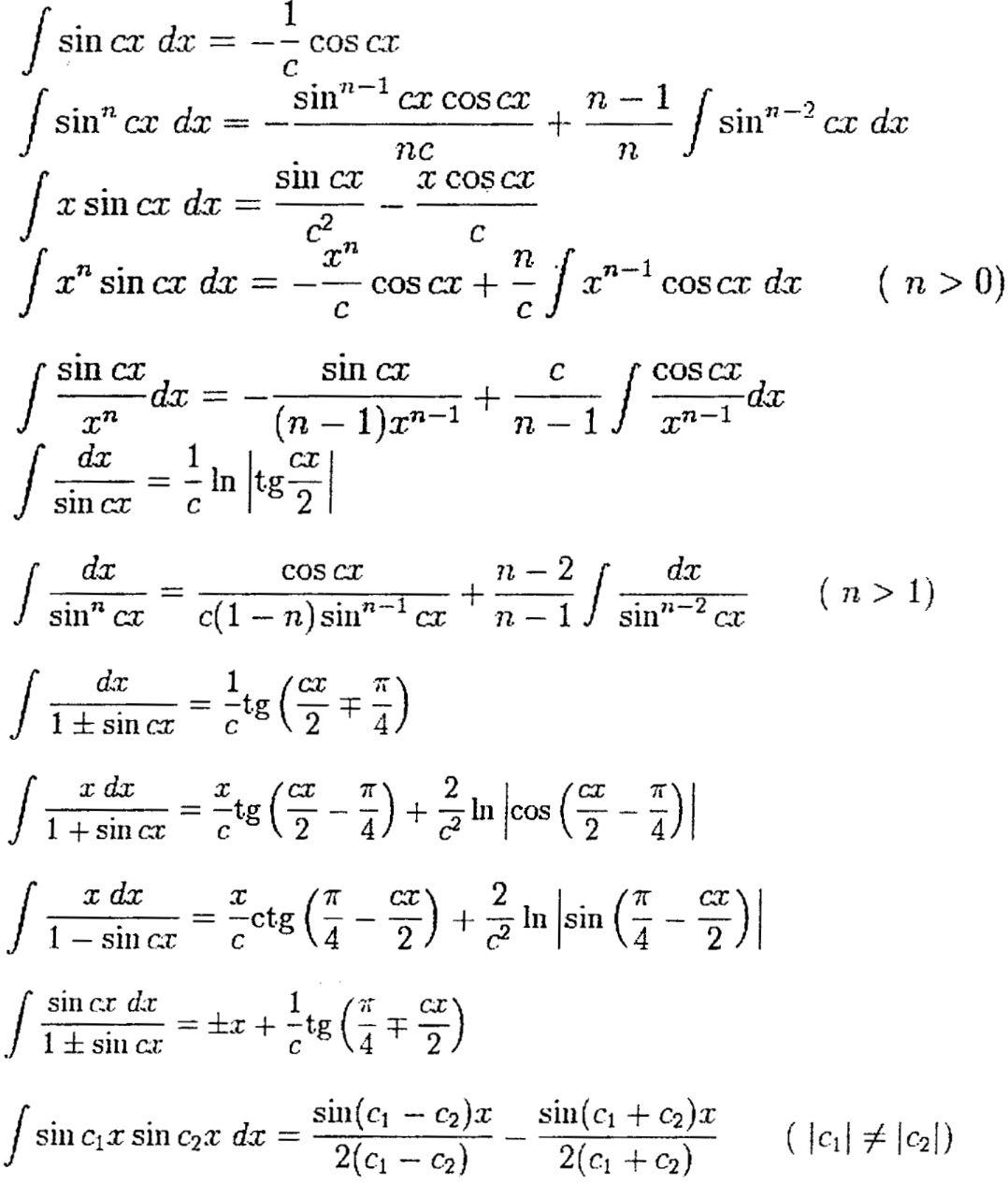Формулы сложения:

Формулы двойного и тройного угла:

Формулы понижения степени:

Формулы приведения:

Наиболее употребительными являются следующие формулы:Формулы суммы и разности синусов:

Формулы суммы и разности косинусов:

Формулы суммы и разности тангенсов:

Преобразование произведения синусов и косинусов в сумму (разность):

Выражение синуса и косинуса через тангенс половинного аргумента:

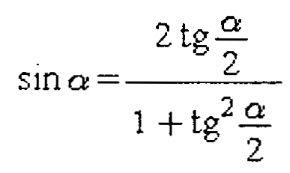
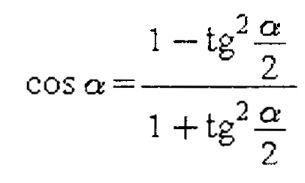
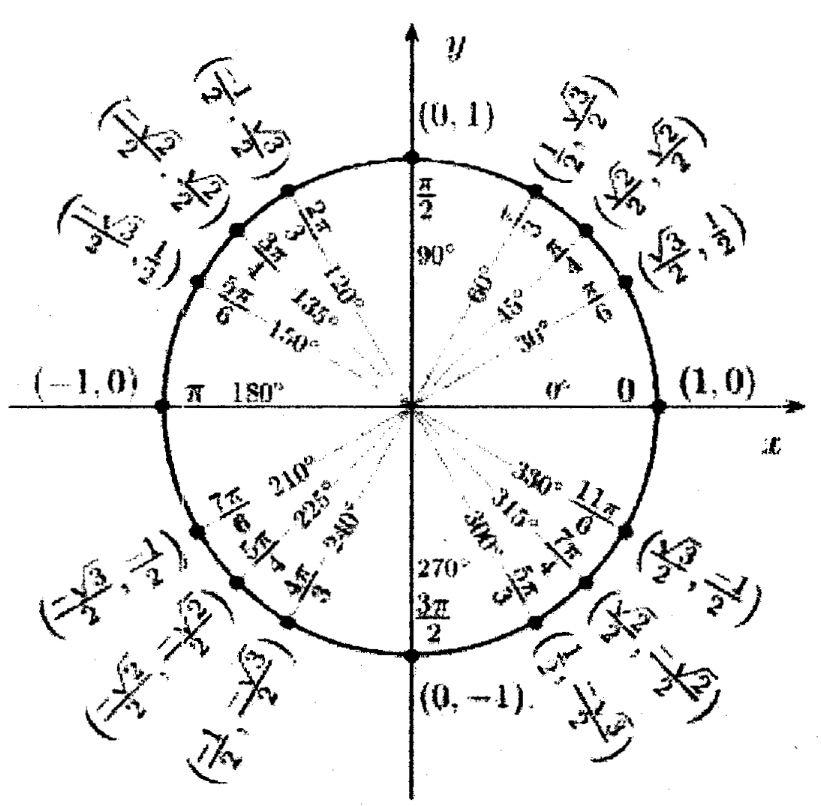
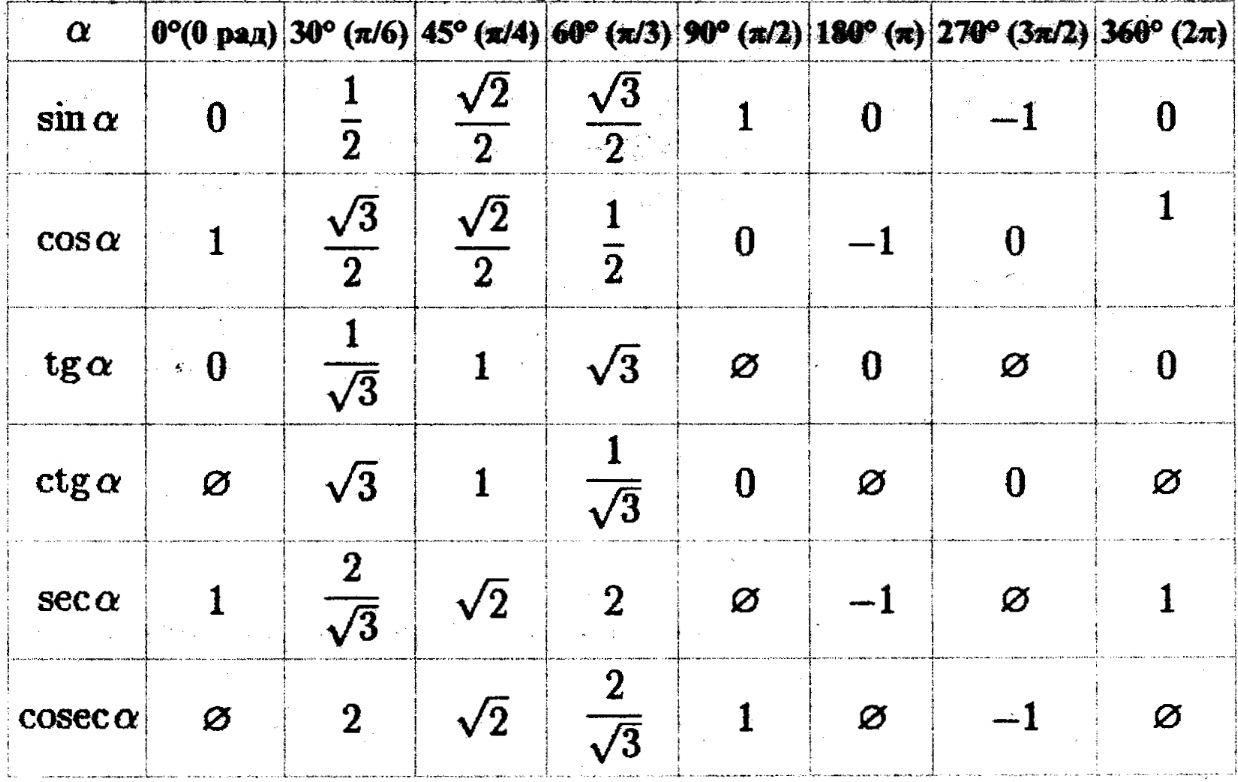
Значения косинуса и синуса на окружности.

причем известен закон изменения переменной х_п , т.е. для каждого натурального числа п можно указать соответствующее значение х_n. Таким образом предполагается, что переменная х_n является функцией от n:

Определение. Постоянное число а называется пределом последовательности x₁ ,x₂,...,х_п,.... или пределом переменной х_п , если для сколь угодно малого положительного числа ε найдется такое натуральное число N (т.е номер N), что все значения переменной x_n , начиная с x_n, отличаются от а по абсолютной величине меньше, чем на ε. Данное определение кратко записывается так:

Здесь п→ ∞ означает, что п неограниченно возрастает. Часто говорят также: х_n стремится к а и пишут x_n→а.

Таким образом, переменная х_n имеет предел а, если абсолютная величина разности между х_n и а в процессе изменения переменной х_п, пробегающей последовательность x₁ , х₂,..., x_n, становится (в момент, когда п = N) и в дальнейшем остается (т.е. для всех п > N) меньше заданного положительного числа ε.

Чем меньшим будет выбрано ε, тем большим будет число N. При n>N выполняется неравенство (2), но для того, чтобы число а было пределом переменной х_n необходимо, чтобы такое число N нашлось, как бы ни мало было число ε.

Но не всякая переменная имеет предел. Так, переменная х_n , принимающая последовательно значения

Предел последовательности

Пусть переменная величина х_n принимает бесконечную последовательность значений

при всех n ≥ N, или, что то же самое,

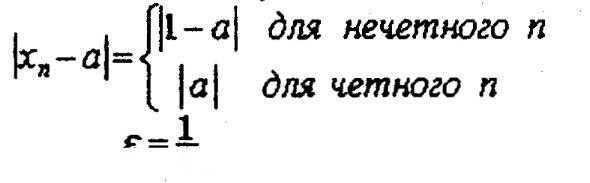
Рассмотрим пример, когда Тогда не существует такого номера N, что для n ≥ N всегда выполнялось бы равенство

1, 0, 1, 0,..., 1, 0,..., предела не имеет, так как в данном случае для любого постоянного числа

Теорема. Переменная х_n может иметь только один предел.(без доказательства)

Арифметическая прогрессия

Арифметическая прогрессия - арифметический ряд первого порядка -последовательность чисел, в которой каждый член (начиная со второго)получается из предыдущего путем прибавления к нему одного и того жечисла называемого разностью этой арифметической прогрессии.

Каждая арифметическая прогрессия имеет вид а, а + d, а + 2d, а + 3d, ...

Общий член арифметической прогрессии а_n = а₁ + d(n - 1)

Характеристическое свойство арифметической профессии

Если разность арифметической прогрессии d > 0, то прогрессия называетсявозрастающей, если d < 0 - убывающей.

Простейший пример арифметической прогрессии - натуральный ряд чисе;1,2,3,..., n,...

Число членов арифметической прогрессии может быть ограниченным либонеограниченным.

Если арифметическая прогрессия содержит n членов, то ее сумму можновычислить по формуле S_n = (a₁ + а_n)*п /2

Пример: 1, 3, 5, 7, 9, 11, 13... - арифметическая прогрессия.

Геометрическая прогрессия

Геометрическая прогрессия - числовая последовательность, каждый членкоторой, начинается со второго, равен предыдущему, умноженному нанекоторое отличное от нуля постоянное число.

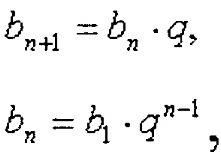
для бесконечно убывающей прогрессии

Пример: 2, 8, 32,128,..., - геометрическая прогрессия. Постоянное число q,называется знаменателем геометрической профессии: q = 4.

Пример: Закон Вебера — Фехнера — открытый Э.Г.Вебером и развитыйГ.Т.Фехнером - основной психофизиологический закон, согласно которомупри увеличении силы воздействия в геометрической прогрессии (1, 2, 4, 8,16 и т.д.) интенсивность ощущения увеличивается в арифметическойпрогрессии (0, 1, 2, 3, 4 и т.д.);

Дополнительный список интегралов (первообразных функций)

Интегралы от экспоненциальной функции.

Интегралы, содержащие только sin

(n >0)