
- •1. Методы оценки сложности и эффективности алгоритмов и структур данных.
- •2. Линейный однонаправленный список, представление и реализация.
- •3. Стек, очередь и дек.
- •4.Мультисписки. Слоеные списки. Иерархические списки.
- •5.Нотации алгебраических выражений.
- •6. Поиск в линейных структурах данных (последовательный поиск, барьеры, бинарный поиск, метод интерполяций)
- •7. Хеширование при хранении и поиске данных. Возникновение и разрешение коллизий.
- •8. Представления и реализации бинарных деревьев, обходы бинарных деревьев.
- •9. Бинарные деревья поиска.
- •10. Алгоритмы построения идеально сбалансированного дерева. Алгоритм построения лозы бинарного дерева.
- •Int* keys; // An array of keys
- •Int t; // Minimum degree (defines the range for number
- •Int n; // Current number of keys
- •13. Графы, способы представления.
- •14. Сортировка вставками (включением),сортировка Шелла.
- •15. Сортировка обменами, шейкерная сортировка.
- •16.Сортировка выбором.
- •17. Сортировка подсчетом. (Требуется проверка)
- •18. Быстрая сортировка Хоара.
- •19. Карманная сортировка, поразрядная сортировка.
- •20. Турнирная сортировка.
- •21. Пирамидальная сортировка.
- •22. Внешняя сортировка, прямое слияние, естественное слияние.
- •23. Алгоритмы поиска в тексте.Прямой поиск, алгоритм Рабина-Карпа
- •24. Алгоритмы поиска в тексте, алгоритм Боуера-Мура.
- •25. Файловые структуры данных. Классификация файлов. Индексные файлы. Инвертированные списки.
18. Быстрая сортировка Хоара.
Алгоритм:
1. вводятся указатели left и right для обозначения начального и конечного элементов последовательности, а также опорный элемент mid;
2. вычисляется значение опорного элемента (left+right)/2, и заносится в переменную mid;
3. указатель left смещается с шагом в 1 элемент к концу массива до тех пор, пока arr[left]<mid. А указатель last смещается от конца массива к его началу, пока arr[right]>mid;
3. каждые два найденных элемента меняются местами;
4. пункты 3 и 4 выполняются до тех пор, пока left<=right.
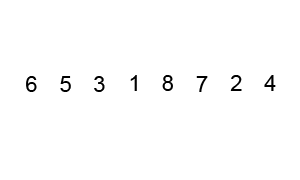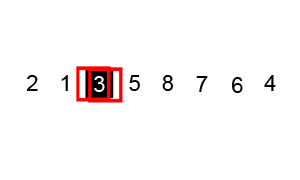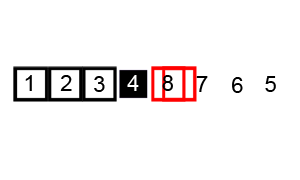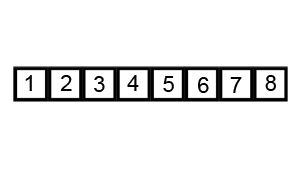
void qsort(int* arr, const int size)
{
int left = 0;
int right = size - 1;
int mid = arr[size / 2];
do
{
while (arr[left] < mid)
left++;
while (arr[right] > mid)
right--;
if (left <= right) std::swap(arr[left++], arr[right--]);
} while (left <= right);
if (right > 0) qsort(arr, right + 1);
if (left < size) qsort(&arr[left], size - left);
}
худший случай: О( )
средний случай: О(N log(N))
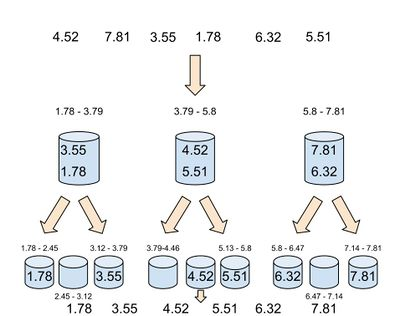
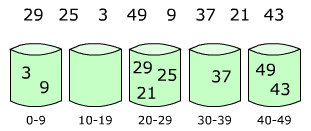
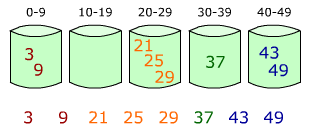
19. Карманная сортировка, поразрядная сортировка.
20. Турнирная сортировка.
Основная идея Tournamentsort заключается в использовании относительно небольшой (по сравнению с основным массивом) вспомогательной кучи, которая выполняет роль приоритетной очереди. В этой куче(дереве) сравниваются элементы на нижних уровнях, в результате чего меньшие элементы поднимаются наверх, а в корень всплывает текущий минимум из той порции элементов массива, которые попали в эту кучу. Минимум переносится в дополнительный массив «победителей», в результате чего в куче происходит сравнение/перемещение оставшихся элементов — и вот уже в корне дерева новый минимум.
Перенос минимумов в дополнительный массив приводит к тому, что в куче появляются вакантные места для следующих элементов основного массива — в результате чего в порядке очереди обрабатываются все элементы.
На каждом из n шагов, требуемых для сортировки массива, нужно log n (двоичный) сравнений. Следовательно, всего потребуется nlog n сравнений, но для представления дерева понадобится 2n - 1 дополнительных единиц памяти.

21. Пирамидальная сортировка.
Пирамидальная сортировка (Heapsort, «Сортировка кучей») — алгоритм сортировки, работающий в худшем, в среднем и в лучшем случае (то есть гарантированно за n*logn операций при сортировке n элементов.
Его идея состоит в том, что вместо полного дерева сравнения исходный массив a[1], a[2], ..., a[n] преобразуется в пирамиду, обладающую тем свойством, что для каждого a[i] выполняются условия a[i] <= a[2i] и a[i] <= a[2i+1]. Затем пирамида используется для сортировки.
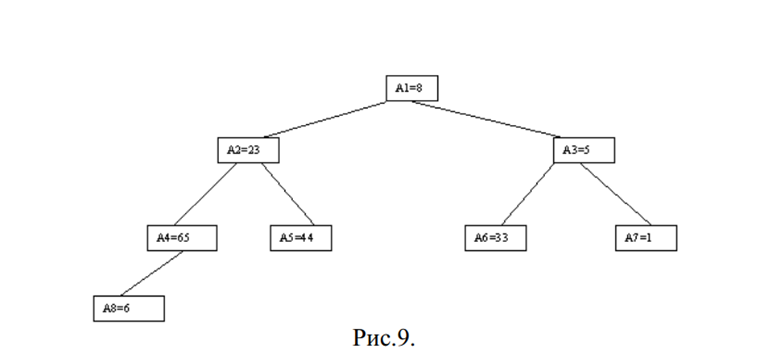
Элементы, для которых существенны ограничения пирамиды: a[n/2], a[n/2-1], ..., a[1] для массивов с четным числом элементов и элементы a[(n-1)/2], a[(n-1)/2-1], ..., a[1] для массивов с нечетным числом элементов Пусть i - наибольший индекс из них. Тогда берется элемент a[i] в построенном дереве и для него выполняется процедура просеивания, состоящая в том, что выбирается ветвь дерева, соответствующая min(a[2i], a[2i+1]), и значение a[i] меняется местами со значением соответствующего элемента.
Флойд предложил метод построения пирамиды без явного построения дерева (хотя метод основан на тех же идеях).

