Пересечение поверхностей геометрических тел плоскостью

При пересечении любой поверхности плоскостью получается некоторого вида плоская фигура, называемая сечением.

Под сечением понимают ту часть секущей плоскости, которая находится внутри рассеченного тела и ограничена линией сечения. Линией сечения тела плоскостью называется контур этого сечения.

Плоскости, которые пересекают поверхности, называют секущими.

Пересечение многогранников плоскостью

При пересечении многогранников секущей плоскостью в сечении получаем многоугольник. Вершинами этого многоугольника являются точки пересечения ребер с секущей плоскостью. На рис.115 пирамида пересечена фронтально-проецирующей плоскостью. В сечении получили треугольник KLM.

На рис.116,117 приведен пример пересечения призмы фронтально-проецирующей плоскостью. В сечении получаем треугольник 123.

Пересечение поверхностей вращения секущей плоскостью

Для решения подобных задач необходимо на поверхности цилиндра или конуса провести семейство образующих (сетку образующих). Как правило, достаточно 8-12 образующих. В остальном алгоритм такой же, как и для гранных тел.

Рис.115

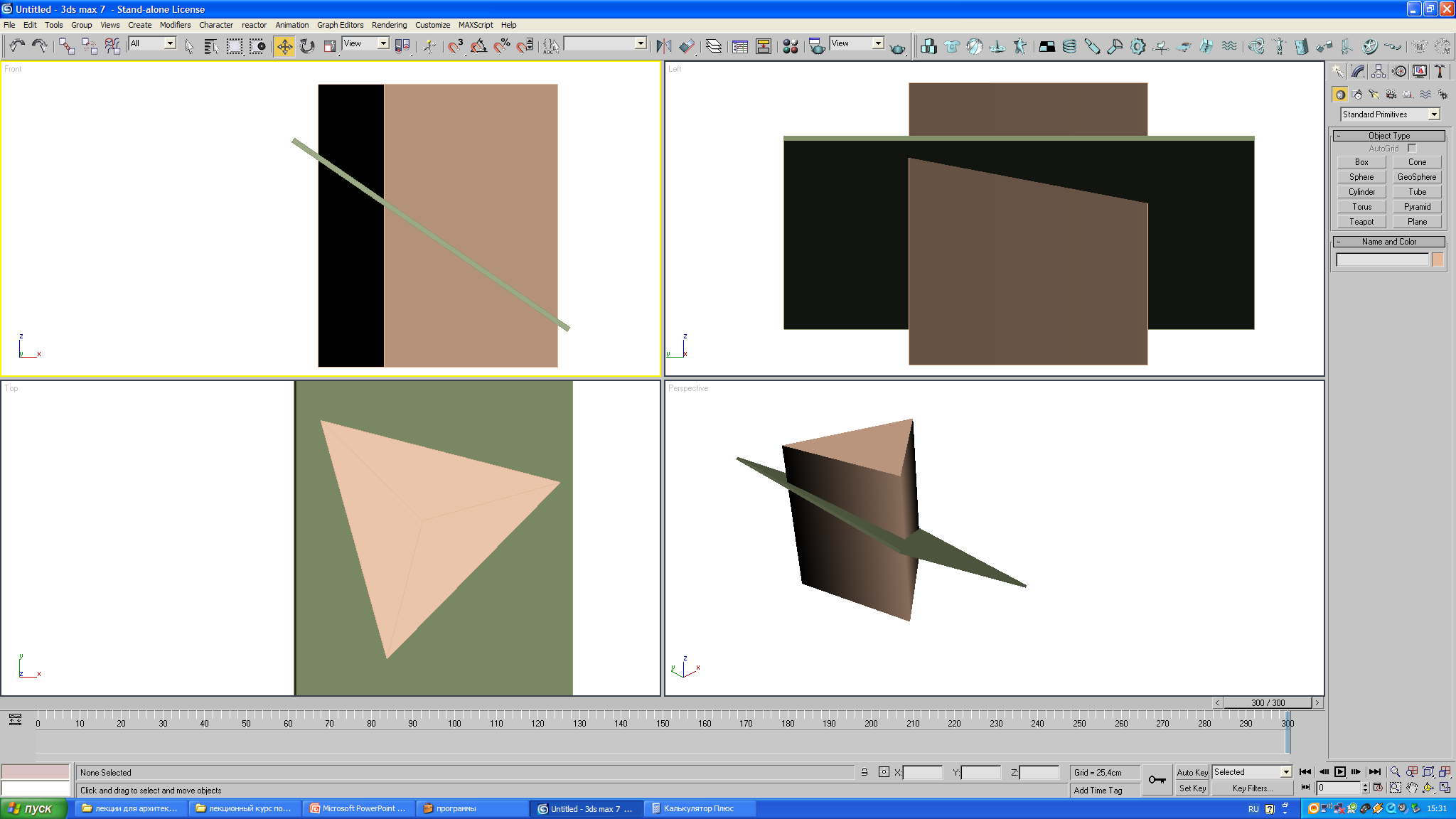
Рис.116 Рис.117

Сечение конуса плоскостью частного положения

При пересечении конуса секущей плоскостью (1), проходящей через вершину, в сечении получаем треугольник. Плоскость (2), параллельная основанию, в сечении дает окружность. Плоскость (3) в сечении дает эллипс. Плоскость (5), параллельная одной образующей, дает в сечении параболу. Плоскость (4), параллельная двум образующим, в сечении дает гиперболу (рис.118, 119,120,121,122).

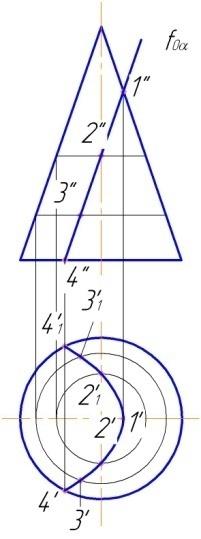
Рис.118

Рис.119

Рис.120

Рис.121

Рис.122

Рассмотрим подробно построение линии пересечения поверхности конуса с плоскостью (рис.123).

Рис.123

Задан конус и плоскость частного положения, в данной задаче плоскость фронтально-проецирующая απ₂, f_оα – собирающий след. Линия пересечения поверхности конуса с фронтально-проецирующей плоскостью представляет собой эллипс. Эллипс – это лекальная кривая, которая строится минимум по 8 точкам. Фронтальная проекция эллипса совпадает с фронтальным следом f_оα.

Рис.120

1. Возьмем ряд точек на f_оα и найдем их горизонтальные проекции. Отметим характерные фронтальные проекции A'' и B'' , C'' и D''. Остальные точки можно выбрать произвольно. Точка лежит на поверхности, если она принадлежит линии, лежащей на этой поверхности (рис.124). Горизонтальные проекции A' и B' получим на образующих, совпадающих с осью симметрии.

2. Для получения горизонтальных проекций C' и D' проведем параллельно основанию линию, горизонтальная проекция которой является окружностью, и на ней отметим C' и D'.

3. Фронтальные проекции M'' и N'' выбрали произвольно на собирающем следе f_оα. Для нахождения горизонтальных проекций M', N' проведем линию параллельно основанию, горизонтальная проекция которой является также окружностью.

4. Полученные горизонтальные проекции точек надо соединить плавной кривой от руки, а затем обвести по лекалу (рис.125).

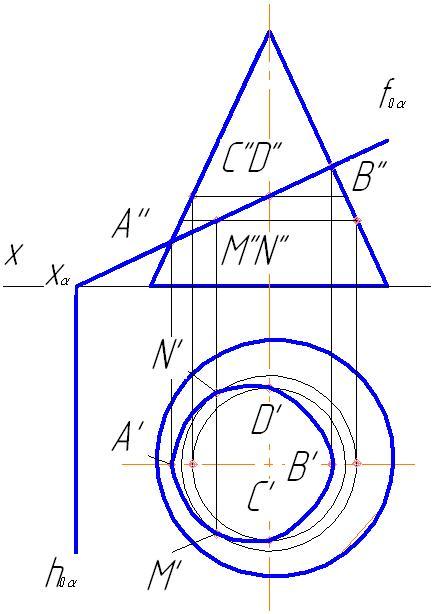
Рис.125