3.1. Определение уравнения линейной регрессии

В качестве базисных возьмем следующий набор функций: 1, ,,. Тогда , и уравнение (1) примет вид

.

Для линейной зависимости определение коэффициентов уравнения регрессии и оценку значимости факторов выделим блок ячеек размером 5 на ,в списке функций находим процедуру = ЛИНЕЙН. В появившемся окне вводим 4 аргумента:

• одномерный массив значений отклика ;

• двумерный массив значений факторов ,,;

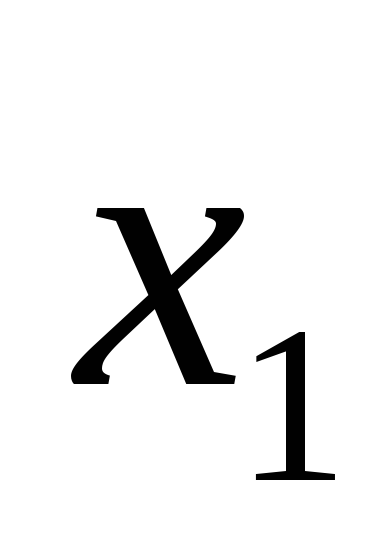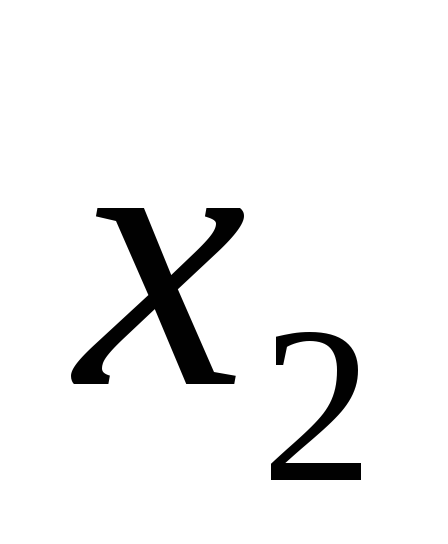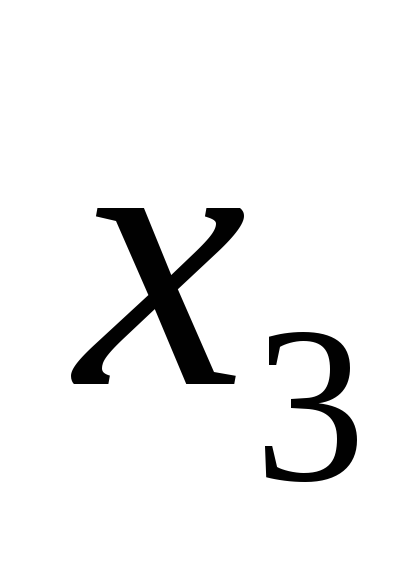• значение ИСТИНА (или число 1), если в число базисных функций включена функция, тождественно равная 1, или значение ЛОЖЬ (или число 0), если функция, равная 1, отсутствует среди набора базисных функций. В первом случае в уравнении регрессии будет присутствовать свободный член, а во втором случае он будет отсутствовать;

• значение ИСТИНА (или число 1), если требуется вычислить дополнительную статистику, или значение ЛОЖЬ (или число 0), если требуется вычислить только коэффициенты уравнения регрессии.

Затем нажимаем клавиши “Ctrl”+”Shift”+”Enter” .Результаты расчетов отображаются в виде табл.3.

Таблица 3

	I	J	K	L
3	53,997251	71,36249	61,33753	-3933,08
4	11,774997	13,51732	2,535307	427,7162
5	0,9307504	159,9589	#Н/Д	#Н/Д
6	206,08807	46	#Н/Д	#Н/Д
7	15819430	1176995	#Н/Д	#Н/Д

В блоке ячеек I3 : L3 содержатся коэффициенты уравнения линейной регрессии

, ,,(коэффициенты следуют в обратном порядке), а само уравнение имеет вид

(7)

В блоке ячеек I4 : L4 находятся среднеквадратические отклонения этих коэффициентов:

, ,,.

3.2. Определение коэффициента детерминации и проверка адекватности математической модели

Ячейка I5 содержит коэффициент детерминации уравнения регрессии: , что свидетельствует о высокой коррелированности теоретических значений, полученных по функции, с фактическими данными. В 93 % случаев изменения х приводят к изменению y. Другими словами – точность подбора уравнения регрессии – высокая.

В ячейке J5 содержится стандартная ошибка для оценки :

.

Ячейка I6 хранит значение F-статистики, которая используется для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимыми переменными случайной или нет: . ЯчейкаJ6 содержит число степеней свободы, равное .

В ячейках I7 и J7 находятся соответственно сумма квадратов, обусловленная моделью , и сумма квадратов ошибок.

Для проверки адекватности уравнения (7) определим критическое значение F-распределения для уровня значимостии степеней свободы:и. Соответствующая формула вExcel имеет вид

= FРАСПОБР(0,05; 3; 46).

В результате получим, что . Так как, то построенная математическая модель в виде уравнения (7) адекватна опытным данным.

3.3. Определение уравнения регрессии с квадратичными членами

К базисным функциям 1, ,,добавим еще набор квадратичных функций,,,,,. Тогда , и уравнение (1) примет вид

.

На новом листе Excel произведем расчет значений параметров, включающих как линейные, так и квадратичные члены (см.табл.4).

Таблица 4

	A	B	C	D	E	F	G	H	I	J	K
1	№ лес-ва	Возр.	Выс.	Диам.							Запас
2
3	1	71	17,6	23,3	5041	1249,6	1654,3	309,76	410,08	542,89	2849
4	2	65	18,8	21,1	4225	1222	1371,5	353,44	396,68	445,21	2748
5	3	60	16,5	23	3600	990	1380	272,25	379,5	529	1941
6	4	89	16,8	21	7921	1495,2	1869	282,24	352,8	441	4027
7	5	86	16,6	18,3	7396	1427,6	1573,8	275,56	303,78	334,89	3456
8	6	74	20,6	18,6	5476	1524,4	1376,4	424,36	383,16	345,96	2927
9	7	73	21	19,6	5329	1533	1430,8	441	411,6	384,16	3248
10	8	73	16,6	23,6	5329	1211,8	1722,8	275,56	391,76	556,96	2900
11	9	76	20,3	20,8	5776	1542,8	1580,8	412,09	422,24	432,64	3467
12	10	62	19,1	24,1	3844	1184,2	1494,2	364,81	460,31	580,81	2737
13	11	74	20,5	19,3	5476	1517	1428,2	420,25	395,65	372,49	3005
14	12	79	18,1	22	6241	1429,9	1738	327,61	398,2	484	3354
15	13	84	20,3	23,3	7056	1705,2	1957,2	412,09	472,99	542,89	4003
16	14	71	18,3	19,8	5041	1299,3	1405,8	334,89	362,34	392,04	2815
17	15	65	20,5	23,8	4225	1332,5	1547	420,25	487,9	566,44	2959
18	16	72	20,8	20,5	5184	1497,6	1476	432,64	426,4	420,25	3338
19	17	84	20,8	21,1	7056	1747,2	1772,4	432,64	438,88	445,21	3856
20	18	72	16,8	19,3	5184	1209,6	1389,6	282,24	324,24	372,49	2811
21	19	72	19	18,3	5184	1368	1317,6	361	347,7	334,89	2586
22	20	60	16,8	21,8	3600	1008	1308	282,24	366,24	475,24	2273
23	21	71	21,1	21,6	5041	1498,1	1533,6	445,21	455,76	466,56	2770
24	22	89	18,3	24,1	7921	1628,7	2144,9	334,89	441,03	580,81	3978
25	23	76	18,1	19,8	5776	1375,6	1504,8	327,61	358,38	392,04	3094
26	24	72	16,1	21,6	5184	1159,2	1555,2	259,21	347,76	466,56	2749
27	25	84	21,8	18,3	7056	1831,2	1537,2	475,24	398,94	334,89	3467
28	26	74	20,8	22,1	5476	1539,2	1635,4	432,64	459,68	488,41	3442
29	27	71	18,6	21,5	5041	1320,6	1526,5	345,96	399,9	462,25	2925
30	28	81	17,6	21,3	6561	1425,6	1725,3	309,76	374,88	453,69	3508
31	29	61	20,3	24,1	3721	1238,3	1470,1	412,09	489,23	580,81	2517
32	30	87	17,6	22,6	7569	1531,2	1966,2	309,76	397,76	510,76	3966
33	31	67	17,3	19,5	4489	1159,1	1306,5	299,29	337,35	380,25	2466
34	32	85	19,5	24,1	7225	1657,5	2048,5	380,25	469,95	580,81	4083
35	33	61	21,8	23,1	3721	1329,8	1409,1	475,24	503,58	533,61	2786
36	34	71	17,5	19,1	5041	1242,5	1356,1	306,25	334,25	364,81	2885
37	35	85	21,6	21,1	7225	1836	1793,5	466,56	455,76	445,21	4127
38	36	68	17,5	20,6	4624	1190	1400,8	306,25	360,5	424,36	2417
39	37	83	18,8	24,6	6889	1560,4	2041,8	353,44	462,48	605,16	3473
40	38	61	19,8	19,6	3721	1207,8	1195,6	392,04	388,08	384,16	2304
41	39	71	21,1	20,5	5041	1498,1	1455,5	445,21	432,55	420,25	2896
42	40	89	19,6	23,3	7921	1744,4	2073,7	384,16	456,68	542,89	4235
43	41	81	16,8	24,1	6561	1360,8	1952,1	282,24	404,88	580,81	3695
44	42	66	21,1	21,3	4356	1392,6	1405,8	445,21	449,43	453,69	2565
45	43	68	19,5	21,1	4624	1326	1434,8	380,25	411,45	445,21	2988
46	44	73	17,5	24,6	5329	1277,5	1795,8	306,25	430,5	605,16	2963
47	45	88	18,5	18,1	7744	1628	1592,8	342,25	334,85	327,61	3825
48	46	88	21	23,8	7744	1848	2094,4	441	499,8	566,44	4249
49	47	75	17,5	22,6	5625	1312,5	1695	306,25	395,5	510,76	3108
50	48	88	20,8	19,5	7744	1830,4	1716	432,64	405,6	380,25	4016
51	49	67	18,6	24,1	4489	1246,2	1614,7	345,96	448,26	580,81	2743
52	50	61	21	23,1	3721	1281	1409,1	441	485,1	533,61	2405

Массив данных, подлежащих обработке, содержится в блоке ячеек B3 : K52. Для определения коэффициентов уравнения регрессии выделим блок ячеек размером 5 на 10. В списке функций находим процедуру = ЛИНЕЙН. В качестве аргументов вводим соответственно:

• одномерный массив значений отклика K3 : K52;

• двумерный массив значений факторов B3 : J52;

• значение ИСТИНА (или число 1),

• значение ИСТИНА (или число 1).

Нажатие клавиш “Ctrl”+”Shift”+”Enter” приводит к появлению данных, как показано в табл.5.

Таблица 5

	O	P	Q	R	S	T	U	V	W	X
3	-17,4652	10,7731	-10,8032	-1,00239	-0,28845	0,15994	672,6396	270,2993	66,44171	-12611,27
4	7,03865	7,920696	10,38735	1,425852	1,510622	0,322191	389,9628	470,8119	65,91671	8179,3968
5	0,944897	153,0157	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д
6	44,16037	40	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д
7	16059873	936552	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д

В блоке ячеек O3 : X3 содержатся коэффициенты уравнения линейной регрессии , а само уравнение имеет вид

(8)

В блоке ячеек O4 : X4 содержатся среднеквадратические отклонения этих коэффициентов:

, ,,,,,,,,.