
материалы по экзамену теплотехника
.docТеплопрово́дность — это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.
Теплопроводностью называется также количественная характеристика способности тела проводить тепло. В сравнении тепловых цепей с электрическими это аналог проводимости.
Способность вещества проводить тепло характеризуется коэффициентом теплопроводности (удельной теплопроводностью). Численно эта характеристика равна количеству теплоты, проходящей через образец материала толщиной 1 м, площадью 1 м2, за единицу времени (секунду) при единичном температурном градиенте.
Закон теплопроводности Фурье
В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:
![]()
где
![]() —
вектор плотности теплового потока —
количество энергии, проходящей в единицу
времени через единицу площади,
перпендикулярной каждой оси,
—
вектор плотности теплового потока —
количество энергии, проходящей в единицу
времени через единицу площади,
перпендикулярной каждой оси,
![]() —
коэффициент
теплопроводности
(удельная теплопроводность),
—
коэффициент
теплопроводности
(удельная теплопроводность),
![]() —
температура. Минус в правой части
показывает, что тепловой поток направлен
противоположно вектору grad T (то есть в
сторону скорейшего убывания температуры).
Это выражение известно как закон
теплопроводности Фурье
—
температура. Минус в правой части
показывает, что тепловой поток направлен
противоположно вектору grad T (то есть в
сторону скорейшего убывания температуры).
Это выражение известно как закон
теплопроводности Фурье
В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):
![]()
где
![]() —
полная мощность тепловых потерь,
—
полная мощность тепловых потерь,
![]() —
площадь сечения параллелепипеда,
—
площадь сечения параллелепипеда,
![]() —
перепад температур граней,
—
перепад температур граней,
![]() —
длина параллелепипеда, то есть расстояние
между гранями.
—
длина параллелепипеда, то есть расстояние
между гранями.
Коэффициент теплопроводности измеряется в Вт/(м·K).
Согласно
гипотезе Фурье, количество теплоты
d2Qτ,
проходящее через элемент изотермической
поверхности dF
за промежуток времени dτ,
пропорционально температурному градиенту
![]() :
:
|
|
(9.4) |
Здесь множитель λ называется коэффициентом теплопроводности. Знак минус указывает на то, что теплота передается в направлении уменьшения температуры. Количество теплоты, прошедшее в единицу времени через единицу изотермической поверхности, называется плотностью теплового потока:
|
|
(9.5) |
Проекции вектора q на координатные оси соответственно:
|
|
|
Уравнения (9.4) и (9.5) являются математическим выражением основного закона теплопроводности — закона Фурье.
Граничные условия в свою очередь бывают трех родов:
1) первого рода, задается распределение температуры на поверхности тела в функции времени;
2) второго рода, задается плотность теплового потока для всей поверхности тела в функции времени;
3) третьего рода, задаются температура окружающей среды tж и закон теплоотдачи между поверхностью тела и окружающей средой — закон Ньютона—Рихмана:
|
|
(9.13) |
где tc — температура поверхности тела; α — коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м2·К). Коэффициент теплоотдачи численно равен количеству теплоты, отдаваемому или воспринимаемому единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в один градус. Этот коэффициент учитывает все особенности явлении теплообмена, происходящие между поверхностью тела и окружающей средой. Плотность теплового потока, передаваемого от поверхности тела в окружающую среду,
9.4.3.Теплопроводность через плоскую стенку при граничных условиях первого рода
|
|
|
Рис. 9.2. Однородная плоская стенка |
 )
и отсутствии внутренних источников
теплоты (qv=0)
дифференциальное уравнение теплопроводности
примет вид:
)
и отсутствии внутренних источников
теплоты (qv=0)
дифференциальное уравнение теплопроводности
примет вид:
|
|
(9.16) |
При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки (ось Оx). В этом случае
|
|
|
и дифференциальное уравнение теплопроводности перепишется в виде:
|
|
(9.17) |
Граничные условия первого рода запишутся следующим образом: при x=0 t=tc1; при x=δ t=tc2. Интегрируя уравнение (9.17), находим
|
|
|
После второго интегрирования получаем
|
|
(9.18) |
Постоянные
С1
и С2
определим из граничных условий: при x=0
t=tc1,
С2=tc1;
при x=δ
t=tc2=С1·δ+tc1,
отсюда
 .
Подставляя значения С1
и С2
в уравнение (9.18), получим уравнение
распределения температуры по толщине
стенки:
.
Подставляя значения С1
и С2
в уравнение (9.18), получим уравнение
распределения температуры по толщине
стенки:
|
|
(9.19) |
Для
определения плотности теплового потока,
проходящего через стенку в направлении
оси Оx, воспользуемся законом Фурье,
согласно которому
 .
.
Учитывая,
что
 ,
получим
,
получим
|
|
(9.20) |
Общее количество теплоты, которое передается через поверхность стенки F за время τ,
|
|
(9.21) |
Отношение
![]() называют
тепловой проводимостью стенки, обратную
ей величину
называют
тепловой проводимостью стенки, обратную
ей величину
 -
термическим сопротивлением теплопроводности.
Поскольку величина λ
зависит от температуры, в уравнения
(9.20), (9.21) необходимо подставить коэффициент
теплопроводности λс,
взятый при средней температуре стенки.
-
термическим сопротивлением теплопроводности.
Поскольку величина λ
зависит от температуры, в уравнения
(9.20), (9.21) необходимо подставить коэффициент
теплопроводности λс,
взятый при средней температуре стенки.
Закон Стефана — Больцмана — закон излучения абсолютно чёрного тела. Определяет зависимость мощности излучения абсолютно чёрного тела от его температуры. Формулировка закона:
|
Мощность излучения абсолютно чёрного тела прямо пропорциональна площади поверхности и четвёртой степени температуры тела:
|
где
![]() -
степень черноты (для всех веществ
-
степень черноты (для всех веществ
![]() ,
для абсолютно черного тела
,
для абсолютно черного тела
![]() ).
При помощи закона Планка для излучения,
постоянную
).
При помощи закона Планка для излучения,
постоянную
![]() можно
определить как
можно
определить как
![]()
где
![]() —
постоянная
Планка,
—
постоянная
Планка,
![]() —
постоянная
Больцмана,
—
постоянная
Больцмана,
![]() —
скорость
света.
—
скорость
света.
Численное
значение
![]() Дж·с−1·м−2
· К−4.
Дж·с−1·м−2
· К−4.
Закон Нью́тона — Ри́хмана — эмпирическая закономерность, выражающая тепловой поток между разными телами через температурный напор.
Теплоотдача — это процесс теплообмена между теплоносителем и твёрдым телом.
Теплопередача — это процесс передачи тепла от одной среды к другой через разделяющую их стенку. Закон утверждает, что
-
Плотность теплового потока (выражается в Вт/м²) на границе тел пропорциональна их разности температур (так называемый температурный напор):

В 1893 году Вильгельм Вин, воспользовавшись, помимо классической термодинамики, электромагнитной теорией света, вывел следующую формулу:
где uν — плотность энергии излучения,
ν — частота излучения,
T — температура излучающего тела,
f — функция, зависящая только от частоты и температуры. Вид этой функции невозможно установить, исходя только из термодинамических соображений.
Первая формула Вина справедлива для всех частот.
Для нечёрных тел можно приближённо записать:
![]()
где
![]() —
степень черноты (для всех веществ
—
степень черноты (для всех веществ
![]() ,
для абсолютно чёрного тела
,
для абсолютно чёрного тела
![]() ).
).
Константу
Стефана — Больцмана
![]() можно
теоретически вычислить только из
квантовых соображений, воспользовавшись
формулой Планка.
можно
теоретически вычислить только из
квантовых соображений, воспользовавшись
формулой Планка.
Закон излучения Кирхгофа — физический закон, установленный немецким физиком Кирхгофом в 1859 году.
В современной формулировке закон звучит следующим образом:
Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты и не зависит от их формы и химической природы.
Известно,
что при падении электромагнитного
излучения на некоторое тело часть его
отражается, часть поглощается и часть
может пропускаться. Доля поглощаемого
излучения на данной частоте называется
поглощательной
способностью
тела
![]() .
С другой стороны, каждое нагретое тело
излучает
энергию по некоторому закону
.
С другой стороны, каждое нагретое тело
излучает
энергию по некоторому закону
![]() ,
именуемым излучательной
способностью тела.
,
именуемым излучательной
способностью тела.
Величины
![]() и
и
![]() могут
сильно меняться при переходе от одного
тела к другому, однако согласно закону
излучения Кирхгофа отношение испускательной
и поглощательной способностей не зависит
от природы тела и является универсальной
функцией частоты (длины волны) и
температуры:
могут
сильно меняться при переходе от одного
тела к другому, однако согласно закону
излучения Кирхгофа отношение испускательной
и поглощательной способностей не зависит
от природы тела и является универсальной
функцией частоты (длины волны) и
температуры:
![]()
По
определению, абсолютно
чёрное тело поглощает всё падающее
на него излучение, то есть для него
![]() .
Поэтому функция
.
Поэтому функция
![]() совпадает
с излучательной способностью абсолютно
чёрного тела, описываемой законом
Стефана — Больцмана, вследствие чего
излучательная способность любого тела
может быть найдена исходя лишь из его
поглощательной способности.
совпадает
с излучательной способностью абсолютно
чёрного тела, описываемой законом
Стефана — Больцмана, вследствие чего
излучательная способность любого тела
может быть найдена исходя лишь из его
поглощательной способности.
В действительных условиях работы различных теплообменных устройств теплота передается одновременно теплопроводностью, конвекцией и излучением. Такое явление называется сложным теплообменом.
Теплообменными аппаратами называются устройства, предназначенные для передачи теплоты от одного теплоносителя к другому. В зависимости от способа передачи теплоты они бывают контактными и поверхностными.
|
|
|
Рис. 12.2. Схема регенератора с неподвижной насадкой |
Поверхностные теплообменные аппараты разделяются на регенеративные и рекуперативные. В регенеративных - теплота горячих газов сначала аккумулируется в теплоемкой насадке (кирпичах, керамической сыпучей массе, металлических листах, шарах). Затем передается нагреваемому газу (воздуху) путем его продувания через горячую насадку. Схема регенератора с неподвижной насадкой приведена на рис. 12.2. Непрерывный процесс теплопередачи между теплоносителями по этой схеме осуществляется с помощью двух регенераторов: когда в одном из них происходит охлаждение горячего теплоносителя, в другом нагревается холодный теплоноситель. Затем аппараты переключаются с помощью клапанов 1 и 2, после чего в каждом из них процесс теплопередачи протекает в обратном направлении.
В рекуперативных аппаратах теплота от горячего теплоносителя передается холодному через разделяющую стенку. К таким аппаратам относятся паровые котлы, подогреватели, конденсаторы.
Схема простейшего кожухотрубного рекуперативного теплообменника приведена на рис. 12.3. Кожухотрубные теплообменники состоят из пучка труб 3, концы которых закреплены в специальных трубных решетках 2. Пучок труб расположен внутри общего кожуха 1, причем один из теплоносителей A движется по трубам, а другой B — в пространстве между кожухом и трубами (межтрубном пространстве). Движение жидкости в теплообменных аппаратах осуществляется по трем основным схемам: прямотока, противотока и перекрестного тока. В схеме прямотока горячая и холодная жидкость движутся параллельно в одном направлении, а в схеме противотока — в противоположных направлениях. В схеме перекрестного тока движение одного теплоносителя перпендикулярно движению другого. На практике встречаются более сложные схемы, включающие различные комбинации основных схем.
|
|
|
Рис. 12.3. Схема кожухотрубного рекуперативного теплообменника |
12.5.Конструкторский и поверочный расчёт теплообменных аппаратов
Тепловой расчет теплообменного аппарата может быть проектным, целью которого является определение поверхности теплообмена, и поверочным, в результате которого при известной поверхности нагрева определяются количество передаваемой теплоты и конечные температуры теплоносителей. В обоих случаях основными расчетными уравнениями являются:
уравнение теплопередачи
|
|
(12.11) |
уравнение теплового баланса, которое при условии отсутствия тепловых потерь имеет вид:
|
|
(12.12) |
где G — массовый расход теплоносителя, кг/с; i — удельная энтальпия, Дж/кг. Здесь и далее индексы 1, 2 относятся соответственно к горячей и холодной жидкостям, индексы ', " — к параметрам жидкости на входе в аппарат и на выходе из него. Полагая, что cр=const, уравнение теплового баланса можно записать так:
|
|
(12.13) |
|
|
(12.14) |
то есть в теплообменных аппаратах температуры горячей и холодной жидкостей изменяются пропорционально их расходным теплоемкостям. В общем случае температуры жидкостей внутри теплообменника не остаются постоянными. Поэтому уравнение теплопередачи (12.11) справедливо лишь для элемента поверхности теплообмена dF, то есть
|
|
|
Общий тепловой поток через поверхность теплообмена F определяется как интеграл
|
|
|
Коэффициент теплопередачи k в большинстве случаев изменяется вдоль поверхности теплообмена незначительно, и его можно принять постоянным. Тогда
|
|
(12.15) |
где Δt — среднее значение температурного напора по всей поверхности нагрева.
|
|
|
Рис. 12.4. Характер изменения температур рабочих тел при прямотоке |
|
|
(12.16) |
При этом температура горячей жидкости понизится на dtж1, а холодной - повысится на dtж2. Следовательно
|
|
(12.17) |
Отсюда
|
|
(12.18) |
Изменение температурного напора при этом определится уравнением
|
|
(12.19) |
где
 .
.
Подставив в уравнение (12.19) значение dQ из (12.16), получаем
|
|
(12.20) |
Обозначив tж1—tж2=Δti, перепишем (12.20) в виде:
|
|
(12.21) |
Интегрируя
при постоянных m
и k,
получаем
 или
или
|
|
(12.22) |
где Δt’=t’ж1—t’ж2 и Δt”=t”ж1—t”ж2 температурные напоры на входе и выходе из аппарата.
Перепишем уравнение (12.22) в виде:
|
|
(12.23) |
Из (12.13) и (12.14) найдём
|
|
|
Подставим найденные значения C1 и C2 в (12.23) и получим:
|
|
|
|
|
|
Тогда
|
|
(12.24) |
Однако Q=k·F·Δt. Поэтому
|
|
(12.25) |
Полученное значение температурного напора называется среднелогарифмическим. Точно также выводится формула для среднего температурного напора аппарата с противотоком (рис. 12.5).
|
|
|
Рис. 12.5. Характер изменения температур рабочих тел при противотоке |
|
|
(12.26) |
Сравнение средних температурных напоров показывает, что при одинаковых температурах теплоносителей на входе и выходе из аппарата наибольший температурный напор получается в теплообменнике с противотоком, наименьший — с прямотоком. Благодаря большей величине среднего температурного напора рабочая поверхность теплообменника с противотоком оказывается меньшей, чем с прямотоком. Следует отметить, что в тех случаях, когда расходная теплоемкость одного из теплоносителей значительно отличается от другого, или когда средний температурный напор значительно превышает изменение температуры одного из теплоносителей, обе схемы будут равноценны.

 .
. .
. ;
;
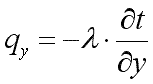 ;
;
 .
.
 .
. ,
,
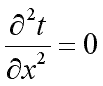 .
. .
.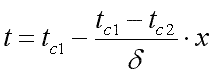 .
. .
.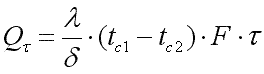 .
.








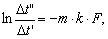
 .
. и
и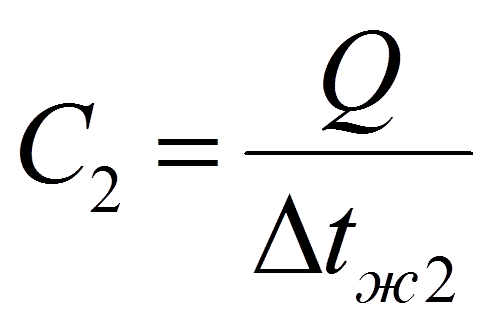 .
.




 .
.