2.2 Качественная характеристика измеряемых величин

Формализованным отражением качественного различия измеряемых величин является их размерность. Размерность обозначается символом dim – от слова dimension (размер, размерность).

Размерность основных физических величин обозначается соответствующими заглавными буквами. Длины, массы и времени, например:

Dim l = L; dim m = M; dim t = T.

При определении размерности производных величин руководствуются следующими правилами:

1. Размерности левой и правой частей уравнений должны совпадать, так как сравниваться между собой могут только одинаковые свойства. Объединяя, левые и правые части уравнений, можно прийти к выводу, что алгебраически суммироваться могут только величины, имеющие одинаковые размерности.

2. Алгебра размерности мультипликативна, то есть состоит из одного единственного действия – умножения, то есть:

   0. Размерность произведения нескольких величин равна произведению их размерностей. Так, если зависимость между величинами Q, A, B, C имеет вид:

Q = A*B*C, то

Dim Q = dim (ABC) = dimA*dimB*dimC

2.2. Размерность частного при делении одной величины на другую равна отношению из размерностей, то есть, если

Q = A/B, то

Dim Q = dimA/dimB

2.3. Размерность любой величины, возведенной в некоторую степень, равна ее размерности в той же степени, то есть, если

Q = Aⁿ, то

Например, если скорость определять по формуле

V = l/t, то

Dim V = dim l / dim t = L / T = L*T^-1

Если сила (F) по второму закону Ньютона

F = m*a,

где a = V / t – ускорение тела, то

Таким образом, всегда можно выразить размерность производной физической величины через размерности основных физических величин с помощью степенного одночлена:

Dim Q = L^∙M^∙T^…,

где L, M, T, … – размерности соответствующих основных физических величин;

, , , … – показатели размерности.

Каждый из показателей размерности может быть положительным или отрицательным, целым и дробным числом, нулем. Если все показатели размерности равны нулю, то такая величина называется безразмерной. Она может быть относительной, определяемой как отношение одноименных величин (например, относительная диэлектрическая проницаемость), и логарифмической, определяемой как логарифм относительной величины (например, логарифм отношения мощностей или напряжений).

Итак, размерность является качественной характеристикой измеряемой величины. Она отражает ее связь с основными величинами и зависит от выбора последних.

Формальное применение алгебры размерностей иногда позволяет определить неизвестную зависимость между физическими величинами.

Пример 1. В результате наблюдений установлено, что при движении тела по окружности сила F, принимающая его к опоре (рисунок 1), в какой-то степени зависит от его скорости V, массы m и радиуса r:

F = m^∙V^∙r^

Определить вид этой зависимости.

Рисунок 1 – Движение по окружности

На основании алгебры размерностей:

Dim F = dim (m^∙V^∙r^) = dim^m ∙ dim^V ∙ dim^r,

Но

Dim F = L*M*T^-2; dim m = M; dim V = L*M^-1; dim r = L

LMT^-2 = M^∙(LT^-1)^∙L^ = L^+ ∙ M^ ∙ T^-

Следовательно, показатели размерности удовлетворяют уравнениям (исходя из первого требования, страница 5)

 +  = 1;  = 1; - = -2

 = 1;  = 2;  = -1

К выводу этой зависимости на основе законов техники был близок Галилей, но первый ее установил Гюйгенс.

Теория размерностей повсеместно применяется для оперативной проверки правильности сложных формул. Если размерности левой и правой частей уравнения не совпадают, то есть не выполняется правило 1 , то в выводе формулы следует искать ошибку.

Пример 2. С помощью размерностей проверить правильность различных зависимостей дальности полета снаряда.

Решение: а) Путь S, как известно, равен скорость (V) умноженная на время:

S = V*t

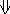
Dim S = dim V * dim t = L * T^-1 * T = L – это метр.

б) в то же время S = V² / g?

где g – ускорение силы тяжести.

Откуда dim S = L² * T^-2 * T² * L^-1 = L – то же метр.

И в первом и во втором случае размерность сохраняется.