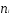практикум 2

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА (практикум)

6.1. Выборочный метод обработки экспериментальных данных

1. В супермаркете проводились наблюдения над числом покупателей, обратившихся в кассу за один час. Наблюдения в течение 30 часов (15 дней в период с 9 до 10 и с 10 до 11 утра) дали следующие результаты:

70, 75, 100, 120, 75, 60, 100, 120, 70, 60, 65, 100, 65, 100, 70, 75, 60, 100, 100, 120, 70, 75, 70, 120, 65, 70, 75, 70, 100,100.

Составить ряд распределения частот (вариационный ряд). Найти размах варьирования, моду и медиану.

2. В ходе проведения эксперимента получен следующий набор данных:

32, 26, 16, 44, 28, 40, 30, 31, 17, 30, 37, 32, 42, 31, 36, 49, 35, 21, 25, 40, 27, 25, 33, 34, 27, 43, 19, 23, 36, 48, 31, 35, 43, 32, 26, 35, 33, 45, 19, 22, 28, 49, 23, 32, 33, 27, 43, 35, 23, 44.

Составить интервальный вариационный ряд, выбрав число частичных интервалов, равное 7. Построить гистограмму частот.

3. Построить полигон частот по данному распределению:

	1	4	5	7
	20	10	14	6

4. Выборка дана в виде распределения частот:

	2	5	7	9	11	13
	10	9	21	25	30	5

Найти распределение относительных частот и построить полигон относительных частот.

6.2. Выборочные числовые характеристики

1. Найти выборочную среднюю по следующим данным: а) длина крыла у 6 пчел (мм): 9,68; 9,81; 9,77; 9,60; 9,61; 9,55; б) длина листьев садовой земляники (см): 5,2; 5,6; 7,1; 6,6; 8,6; 8,2; 7,7; 7,8.

2. Выборка задана рядом распределения частот:

	4	7	10	15
	10	15	20	5

Найти выборочную среднюю и выборочную дисперсию.

3. По выборке объема найдена выборочная дисперсия . Найти исправленную дисперсию.

6.3. Статистические оценки

1. Найти несмещенную оценку дисперсии случайной величины 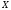на основании данного распределения выборки:

	2	7	9	10
	8	14	10	18

2. Найти доверительный интервал с надежностью 0,95 для оценки математического ожидания нормально распределенной случайной величины , если известны ее среднее квадратическое отклонение , выборочная средняя и объем выборки .

3. По данным выборки объема найдено несмещенное значение выборочного среднего квадратического отклонения 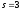нормально распределенной случайной величины . Найти с надежностью 0,99 доверительный интервал для оценки среднего квадратического отклонения случайной величины.

4. Случайная величина 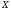распределена по нормальному закону. Статистическое распределение выборки представлено в таблице:

	1	3	5	7	9
	2	5	4	6	3

Найти с надежностью 0,97 доверительный интервал для математического ожидания и с надежностью 0,95 – для оценки среднего квадратического отклонения.

6.4. Проверка статистических гипотез

1. Акционерное общество (АО) выпускает печенье «Русские узоры» в пачках, на которых написано: масса нетто 200 г. Осуществлена выборка для оценки средней массы печенья в пачках, выпущенных московской и санкт-петербургской фабриками АО. Результаты выборок таковы (указана масса пачек печенья «Русские узоры»):

Московская фабрика

201; 195; 197; 199; 202; 198; 199; 203; 195; 196; 198; 199; 194; 203; 195; 202; 197.

Санкт-петербургская фабрика

203; 207; 191; 193; 197; 201; 196; 192; 194; 195; 198; 196.

Предполагая, что случайная величина массы пачки печенья распределена по нормальному закону с одинаковыми дисперсиями, и считая выборки независимыми, определить:

а) выборочные средние и исправленные средние квадратические отклонения массы для каждой фабрики;

б) для 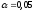значимо или нет различие между выборочными средними (если это различие имеется);

в) является ли величина 200 г математическим ожиданием массы при уровне значимости.

2. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты.

Эмпирические частоты	6	12	16	40	13	8	5
Теоретические частоты	4	11	15	43	15	6	6