6.5. Переходные процессы в цепи с последовательным соединением резистивного, индуктивного и емкостного элементов

Рассмотрим апериодическую разрядку конденсатора. Если ключ К на рис. 6.9 переключить из положения а в положение b, то образуется накоротко замкнутый контур rLC, в котором до коммутации конден- сатор заряжен до напряжения источника U₀. После коммутации в замкнутом контуре rLC протекает свободный процесс, который, согласно второму закону Кирхгофа, описывается однородным уравнением

(6.34)

Так как i_CB = Cdu_CcB/dt,то

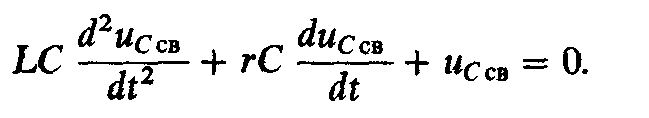(6.35)

Характеристическое уравнение для (6.35) имеет вид

(6.36)

и два корня

(6.37)

Если в колебательном контуре резонансная частота ито выражение для определения корней характеристического уравнения можно переписать:

(6.38)

Характер свободного процесса зависит от вида корней характе­ристического уравнения, которые, в свою очередь, зависят от соотноше­ния параметров цепи г, L, С. Свободный процесс, наблюдаемый в замкнутом rLC-контуре после коммутации, представляет собой апе­риодическую разрядку конденсатора.Апериодической называется разряд­ка конденсатора, заряженного до напряжения U₀, через резистор и индуктивную катушку, когда напряжение на конденсаторе постепенно спадает до нуля. Апериодический процесс разрядки конденсатора имеет место, если корни характеристичес­кого уравнения вещественны, т. е. если в (6.38) r²/(4L²) > 1/LC или r/(2L) > 1/, илиr > 2=r_кр, и по­лучается пара разных корней.

Сопротивление r_кр = 2назы­вается критическим, так как оно яв­ляется наименьшим сопротивлениемrLC-контура, когда еще имеет место апериодический процесс разрядки конденсатора. При корни характеристического уравнения получаются комплексными и сопря­женными. Таким образом, корни характеристического уравнения p₁ и р₂ будут вещественными и различными, если выполняется условие r > r_кр. Если корни различны, то общее решение однородного диф­ференциального уравнения (6.35) имеет вид

(6.39)

где A₁ и A₂ — вещественные постоянные интегрирования, a p₁ и р₂ — вещественные и различные корни, которые должны быть отрицатель­ными, так как свободный процесс должен быть затухающим во вре­мени.

Так как при разрядке конденсатора в накоротко замкнутом конту­ре rLC процесс является свободным, то переходные значения напряжения u_C и тока i равны их свободным значениям, т. е. u_C = u_ccв и i = i_cв. Ток цепи

(6.40)

Подставляя начальные условия (при t = 0 uс = U₀ и i = 0) в (6.39) и (6.40), получаем

(6.41)

Из системы уравнений (6.41) определяем постоянные интегриро­вания:

Подставляя их в (6.39) и (6.40), окончательно получаем

(6.42)

но так как, согласно теореме Виета, произведение корней p₁ и р₂ характеристического уравнения равно его свободному члену [р₁р₂ = 1/(LC)] , то последнее выражение можно записать в виде

(6.43)

Напряжение на индуктивном элементе u_L определяется по формуле

(6.44)

Так как для свободного процесса, имеющего апериодический характер, корни характеристического уравнения должны быть вещественными и различными, то, согласно (6.36) и (6.37), они также всегда должны быть отрицательными.

Как видно из формул (6.42), (6.43) и (6.44), корни характеристи­ческих уравнений входят в показатели экспонент; следовательно, свободные процессы в цепях всегда затухают и тем быстрее, чем больше абсолютное значение корня характеристического уравнения. Если согласно этим формулам характер изменения переходных процессов представить в виде кривых, то каждая из них будет представлять собой сумму двух экспонент с коэффициентами затухания |p₁| и |p₂| соответственно. Значение коэффициентов затухания находят по фор­муле (6.37). Кривые изменения напряжений и их составляющих на емкостном и индуктивном элементах, а также кривые изменения тока и его составляющих приведены на рис. 6.10, а - в. Из рисунка видно, что напряжение на емкостном элементе u_C постепенно уменьшается от начального значения U₀, а ток в начальный отрезок времени, воз­растая от нуля, достигает максимума, а затем, как и u_C, также затухает.

Когда Это означает, что в зави -симостях u_C(t), i(t), u_L(t) состоящих из алгебраической суммы двух экспонент, первая экспонента затухает медленнее, чем вторая. Вследст­вие этого напряжение на емкостном элементе u_C постепенно убывает, оставаясь всегда положительным, так как его первая экспонента поло­жительна и больше второй отрицательной экспоненты.

Кривая тока i (рис. 6.10,б) находится в отрицательной области, так как происходит апериодическая разрядка конденсатора.

Так как ток i = Cdu_C/dt, то максимум кривой тока i(t) и точка перегиба кривой напряжения u_C(t) имеют место в один и тот же момент времени t₁ (рис. 6.10, а, б), а кри­вая u_L(t) в этот момент времени меняет знак, что следует из соотношения u_L = Ldi/dt (рис. 6.10,в). Время t₁ можно найти, приравнивая нулю производную di/dt. На­пряжение на индуктивном элементе возни­кает скачком, принимая в начальный мо­мент (t = 0) значение - U₀, затем умень­шается по абсолютному значению, прохо­дит через нуль при равенстве экспонент и, став положительным, возрастает до некото­рого максимального значения, после кото­рого, уменьшаясь, стремится к нулю.

Следует отметить, что, согласно (6.37), увеличение индуктивности L приводит к уменьшению абсолютных значений p_l и p₂ и, как следствие, к замедлению возрастания тока i и спада напряжения на емкостном элементе u_C.

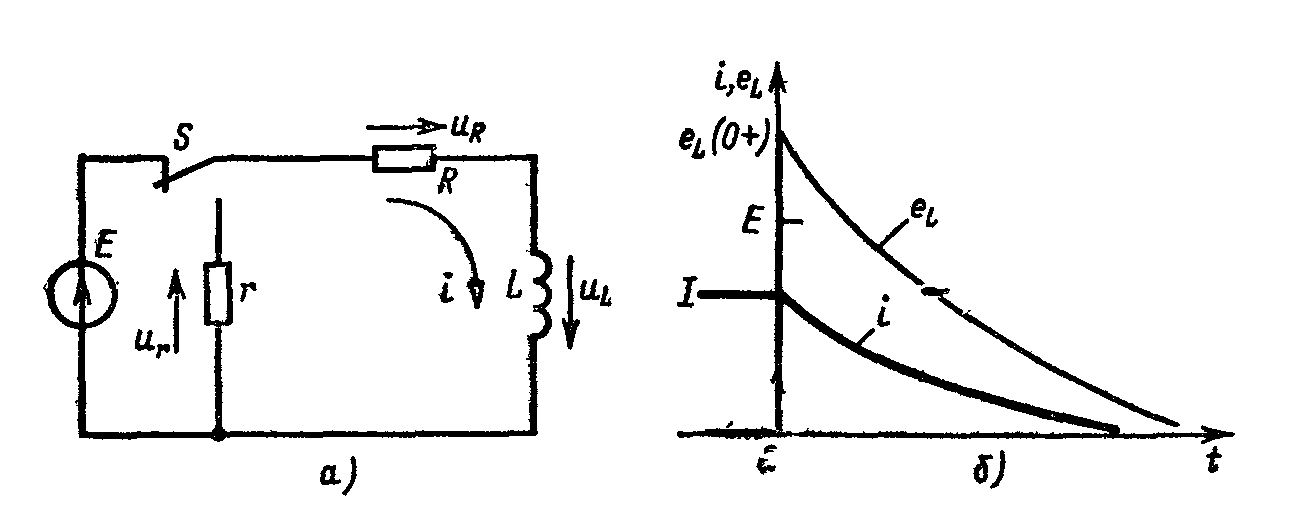
Пример 6.1. Неразветвленная цель R, L (рис. а)) включается на постоянное напряжение U = 10 В. Определить постоянную времени цепи τ

Рисунок к примеру 6.1.

и длительность переходного процесса t_п, если R = 100 Ом, L = 0,l Гн и допуск на отклонение от установившегося значения составляет 1 %.

Решение. Постоянная времени τ=L/R = 0,1/100 = 10^-3 с. Переходный ток i = (U/R)^. (1-е ^-t/^τ) = 0,1(1—e^-t/ ^0,001) А.

Переходный процесс можно считать законченным, когда i(t_п) = 0,1(1—e ^-1000tп)=0,l ^. 0 ,99 А, откуда e^-1000tп = 0,01; 1000t _п = ln100=4,6 и t_п = 4,6^.10^-3 с.

Пример 6.2. Конденсатор емкостью С =15 мкФ заряжен до напряжения U = E = 100 В (рис. а)). После отключения конденсатора от источника,

Рисунок к примеру 6.2.

он медленно разряжается через сопротивление собственной изоляции r. При этом через промежуток времени t_p=42 с напряжение уменьшается в k = 4 раза. Определить постоянную времени переходного процесса τ и сопротивление изоляции r.

Решение. Напряжение на конденсаторе во время его разрядки

u_{c =} Ue^—t/τ. Через t_p, с, напряжение и_с(t_p) = Ue^—tp/τ=U/k , откуда е^tp/τ=k или τ = t_p /lnk = 42/ln4 = 30c.

Сопротивление изоляции r = τ/С =30/15^.10^-6Ом =2 МОм.