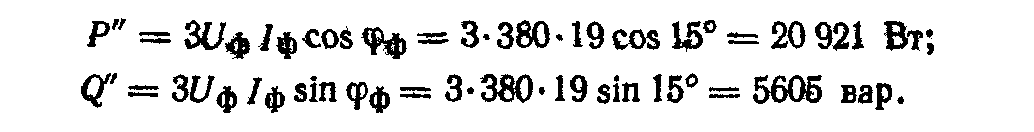5.3. Виды симметричных периодических функций

Периодические несинусоидальные функции, обладающие каким-либо видом симметрии, имеют определенные свойства, которые упрощают разложение этих функций в тригонометрический ряд. Существуют функции, симметричные относительно оси абсцисс, относительно оси ординат, относительно начала координат, а также функции, симметрич­ные как относительно оси абсцисс, так и относительно оси ординат. Рас­смотрим такие функции.

Функция, симметричная относительно оси абсцисс. Функция, удов­летворяющая условию

(5.8)

называется симметричной относительно оси абсцисс (рис. 5.4). Иными словами, функция симметрична относительно оси абсцисс, если ее двум абсциссам, отличающимся на полпериода Т/2, соответствуют равные, но разные по знаку ординаты. Кривая обладает свойством сим­метрии относительно оси абсцисс в том случае, если в результате сме­щения ее положительной полуволны по оси на полпериода, т. е. на Т/2, и зеркального отражения относительно оси t получается изобра­жение отрицательной полуволны.

Такая функция при разложении в ряд Фурье не содержит постоян­ной составляющейA₀ и высших гармоник четного порядка. Докажем это положение. Так как условием симметрии является равенство

•

Последнее равенство имеет место при любых значениях ωt, что возможно только при условии, когда A₀ = 0, А_2m = 0, А_4m = 0 и т. д., т. е. когда нулевая гармоника и амплитуды четных гармоник равны нулю.

Таким образом, функция, симметричная относительно оси абсцисс, при разложении в ряд Фурье содержит только нечетные гармоники.

Следовательно,ряд Фурье такой функции имеет вид

Функция, симметричная относительно оси ординат. Функция, удовлет­воряющая условию

(5.10)

называется симметричной относительно оси ординат (рис. 5.5). Иными словами функция симметрична относительно оси ординат, если двум равным ординатам, соответствуют равные, но разные по знаку абсциссы.

Функция, симметричная относительно оси ординат, при разложе­нии в ряд Фурье не содержит синусов, а содержит только косинусы и постоянную составляющую. Рассмотрим это свойство симметрии.

Итак, условие симметрии f(ωt) = f(-ωt), или f(ωt) - f(-ωt) = 0, где

Следует иметь в виду, что при изменении знака аргумента синусы меняют знак, а косинусы его не меняют, так как cos (- ωt) = cos (ωt). В результате алгебраического сложения уравнений (5.11) и (5.12) имеем

Это равенство будет иметь место при любых значениях ωt, но при условии, когда В_1m = 0, В_2m = 0, В_3m = 0 и т. д. Следовательно, при симметрии функции относительно оси ординат ряд не содержит синусов:

(5.13)

Функция» симметричная относительно начала координат. Функция, у которой точка нуля функции совпадает с началом координат (рис. 5.6) и удовлетворяет условию

(5.14)

называется симметричной относительно начала координат. Согласно (5.14), условие симметрии для данной функции можно также записать в виде

Складывая уравнения (5.11) и (5.12), получим

Это равенство справедливо при условии А₀ = 0, С_1m = 0, С_2m = 0, С_3m = 0 и т. д. Следовательно, функции, симметричные относительно начала координат, не содержат постоянной составляющей и косинусов и могут быть представлены рядом

(5.15)

Функция, симметричная как относительно оси абсцисс, так и начала координат. Если функция симметрична относительно оси абсцисс, то при разложении ее в ряд в нем отсутствуют нулевая и четные гармо­ники, а для функции, симметричной относительно начала координат, кроме того, отсутствуют и косинусоиды. Следовательно, функция, сим­метричная как относительно оси абсцисс, так и начала координат , (рис. 5.7), при разложении в ряд состоит только из синусоид нечетного порядка:

(5.16)

Пример 4.3. К трехпроводной трехфазной линии с линейным на­пряжением 380 В подключен трехфазный приемник с параметрами R=10 Ом, X_L = 10 Ом, Х_с=10 Ом. Рассчитать токи в фазах и в линии, построить совмещенные топографическую диаграмму напряжений и векторную диаграмму токов.

Решение. Сопротивления фаз по модулю одинаковые, но по аргументу разные; следовательно, нагрузка несимметричная и ток, каждой фазы необходимо рассчитать отдельно.

Комплексные сопротивления фаз:

Комплексные линейные напряжения:

Фазные токи:

Линейные токи:

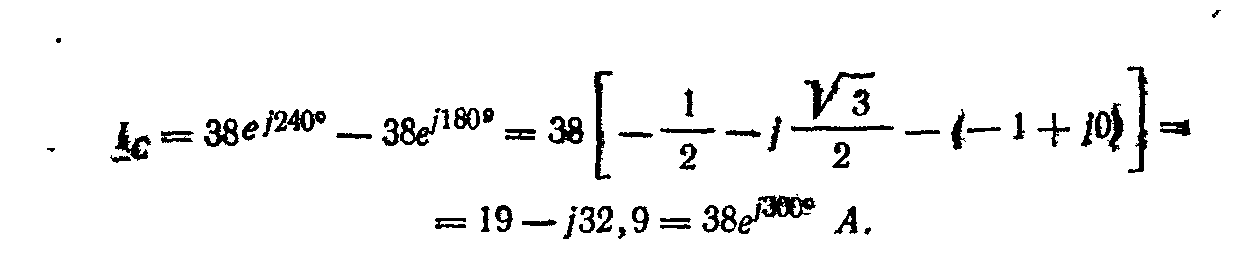
Рисунки к примеру 4.3.

Для построения векторных диаграмм выбираем масштабы напряже­ния и тока. Строим топографическую диаграмму напряжений. Векторы фазных токов I_ab, I_bc, J_ca соот­ветственно откладываем относительно векторов линейных напряжений U_ab, U_bc, U_ca под углами φ_ab= 0, φ_bc = 90°, φ_ca = -90 ^о. За­тем в соответствии строим векторы I_A, I_B, I_C длина и на­правление которых должны соответствовать расчетным данным.

Пример 4.4. К трехфазной линии с U_Л=380 В подключены трехфазный симметричный приемник, фазы которого соединены треугольником, и группа однофазных приемников, соединенных звездой с ней­тральным проводом. Комплексное сопротивление фазы сим­метричного приемника Z_ф = 20 е^j15° Ом. Активные мощности однофазных приемников Р_a=5500 Вт, Р_b=3300 Вт, Р_c=7700 Вт при соsф_ф = 1. Со­противлением проводов можно пренебречь. Определить: фазные и ли­нейные токи симметричного приемника, токи в несимметричных приемниках, суммарные активную, реактивную и полную мощности.

Решение. Фазные напряжения при соединении звездой с нейтральным проводом Uф =U_Л /= 380/= 220 В.

Рисунок к примеру 4.4.

Фазные токи однофазных приемников:

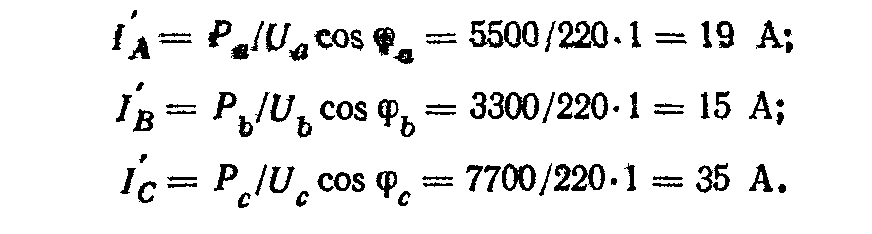
Фазные и линейные токи трехфазного приемника:

и его активная, реактивная и полная мощности: