
- •5.4. Действующие и средние значения несинусоидальных периодических токов и напряжений
- •5.5. Мощность периодического несинусоидального тока
- •Глава 6. Переходные процессы в линейных электрических цепях
- •6.1. Возникновение переходных процессов и законы коммутации
- •6.2. Переходный, принужденный и свободный режимы
- •Контрольные вопросы
6.2. Переходный, принужденный и свободный режимы
Рассмотрим расчет переходных процессов на примере подключения цепи с последовательным соединением резистивного, индуктивного и емкостного элементов к источнику периодически изменяющейся э. д. с. е (рис. 6.1).
Электрическое состояние цепи после коммутации, согласно второму закону Кирхгофа, описывается уравнением
 (6.4)
(6.4)
Здесь i - ток переходного процесса, называемый переходным. После окончания переходного режима наступает принужденный (установившийся) режим, который создается источником периодически изменяющейся э. д. с.
При исследовании переходных процессов необходимо установить порядок уравнения электрического состояния цепи, который равен числу независимых начальных условий для токов индуктивностей и напряжений на емкостях. Для цепи рис. 6.1 переходный процесс описывается уравнением второго порядка, так как значения i и uc можно задать независимо друг от друга:
 (6.5)
(6.5)
Из математики
известно, что решение линейного
дифференциального уравнения с постоянными
коэффициентами представляет собой
сумму двух решений: частного решения
неоднородного уравнения и общего решения
однородного уравнения. Частное решение
описывает принужденный режим, 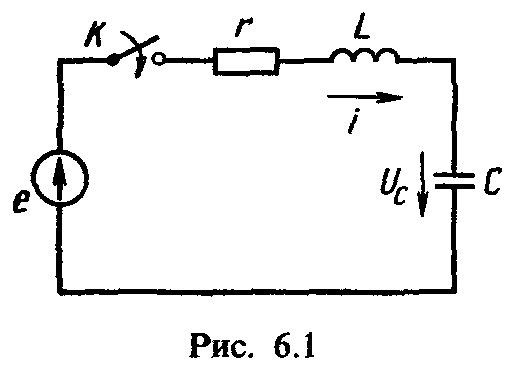 задаваемый
источником энергии, и зависит от вида
функции, стоящей в правой части уравнения.
Если функция правой части уравнения
постоянна или является периодической
функцией времени, то принужденный
ток будет установившимся, а расчет
принужденного режима проводится в
последовательности и по формулам
предыдущих глав.
задаваемый
источником энергии, и зависит от вида
функции, стоящей в правой части уравнения.
Если функция правой части уравнения
постоянна или является периодической
функцией времени, то принужденный
ток будет установившимся, а расчет
принужденного режима проводится в
последовательности и по формулам
предыдущих глав.
Общее решение однородного уравнения описывает переходный процесс, протекающий без воздействия внешних источников, т. е. протекающий за счет энергии, накопленной в индуктивных и .емкостных элементах цепи до начала переходного режима, и имеет одинаковый вид для любого переходного процесса в данной цепи. Это означает, что исследуемая цепь в этом случае освобождается от воздействия внешнего источника энергии, поэтому токи или напряжения, найденные в результате решения однородного уравнения, называются свободными составляющими (или просто свободными). При отсутствии внешних источников энергия, запасенная в цепи, постепенно расходуется и свободная составляющая с течением времени уменьшится до нуля. Для определения свободного тока однородное уравнение, полученное из (6.5), имеет вид
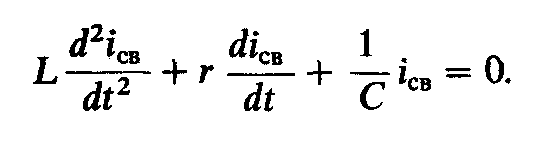 (6.6)
(6.6)
Запишем характеристическое уравнение для (6.6):
 (6.7)
(6.7)
Определив из характеристического уравнения корни p1 и р2, запишем общее решение в виде
![]() (6.8)
(6.8)
где A1 и А2 — постоянные интегрирования, определяемые из начальных условий. Следует отметить, что число слагаемых в (6.8) равно порядку дифференциального уравнения.
Действительное значение тока во время переходного режима равно сумме принужденного и свободного токов:
![]() (6.9)
(6.9)
Аналогично, действительное напряжение на любом участке цепи при переходном режиме равно сумме принужденной и свободной составляющих:
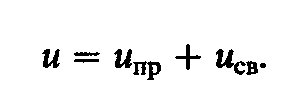 (6.10)
(6.10)
Итак, физически существуют только переходные токи и напряжения, а разложение их на свободные и принужденные составляющие является математическим приемом, позволяющим упростить расчет переходных процессов в линейных цепях, ибо принцип наложения применим лишь к линейным цепям. Основная трудность анализа переходных процессов классическим методом заключается в определении свободных токов и напряжений.
П ример
5.1.На выводах
цепи периодическое несинусоидальное
напряжение
ример
5.1.На выводах
цепи периодическое несинусоидальное
напряжение
![]()
Активное сопротивление R=2 Ом. При основной частоте 1 индуктивное сопротивление ХL1 = 2 Ом, емкостное XC1 = 3 Ом. Определить мгновенные значения всех токов, активную и полную мощности, показания амперметров, измеряющих действующее значение токов.
Рисунок к примеру 5.1.
Решение. Токи определим методом наложения (цифровой индекс у всех величин — номер гармоники). На схеме показаны выбранные положительные направления токов.
Постоянная составляющая тока I0 отсутствует в ветви с конденсатором. Поэтому по закону Ома I0=IL0=U0/R=6/2=3 А {здесь учтено, что для постоянной составляющей индуктивное сопротивление равно нулю).
Суммарное комплексное сопротивление для первой гармоники тока
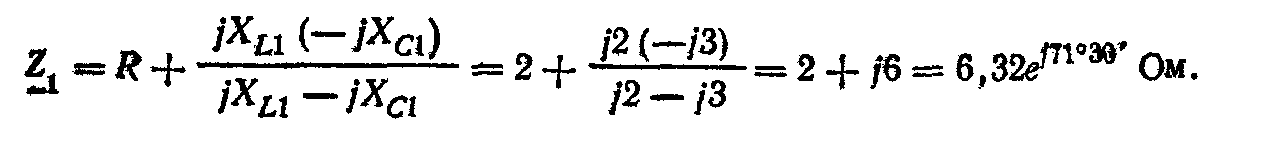
Ток первой гармоники в неразветвленной части цепи

Напряжение первой гармоники на участке ab

Токи первой гармоники в параллельных ветвях:
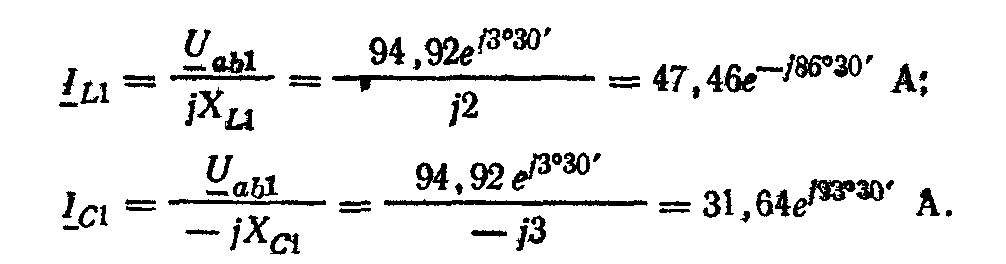
Общее комплексное сопротивление для третьей гармоники тока


Tок третьей гармоники в неразветвленной части цепи
![]()
Напряжение третьей гармоники на участке ab
![]()
Токи третьей гармоники в параллельных ветвях;

Мгновенные и действующие значения токов (показания амперметров):

.
Активная мощность цепи

Полная мощность

