49)Алгебра логики. Принцип и закон двойственности

Алгебра логики – раздел математической логики, в котором изучаются логические операции над высказываниями. Высказывания могут быть истинными, ложными или содержащими истину и ложь в разных соотношениях.

Принцип двойственности: В булевых алгебрах существуют двойственные утверждения, они либо одновременно верны, либо одновременно неверны. Именно, если в формуле, которая верна в некоторой булевой алгебре, поменять все конъюнкции на дизъюнкции, 0 на 1, ≤ на ≥ и наоборот, то получится формула, также истинная в этой булевой алгебре. Это следует из симметричности аксиом относительно таких замен.

Закон двойственности: Формулы А и А^*называются двойственными, если формула А^*получается из формулы А путем замены в ней каждой операции на двойственную.

Имеет место следующий закон двойственности: если формулы А и В равносильны, то равносильны и им двойственные формулы, т.е. А^*ºВ^*.

50)Алгебра логики. Теоремы разложения

Алгебра логики – раздел математической логики, в котором изучаются логические операции над высказываниями. Высказывания могут быть истинными, ложными или содержащими истину и ложь в разных соотношениях.

Разложением Шеннона по переменной называется метод представления булевой функции от переменных в виде суммы двух подфункций от остальных переменных.

Теорема(о разложении функций по переменным, разложение Шеннона). Каждую функцию алгебры логики при любомможно представить в следующей форме:

где дизъюнкция берется по всевозможным наборам значений переменных .Это представление называетсяразложением функции по m переменным .

51) Алгебра логики. Разложение Шеннона

Алгебра логики – раздел математической логики, в котором изучаются логические операции над высказываниями. Высказывания могут быть истинными, ложными или содержащими истину и ложь в разных соотношениях.

Разложением Шеннона по переменной называется метод представления булевой функции от переменных в виде суммы двух подфункций от остальных переменных.

Теорема(о разложении функций по переменным, разложение Шеннона). Каждую функцию алгебры логики при любомможно представить в следующей форме:

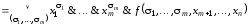
где дизъюнкция берется по всевозможным наборам значений переменных .Это представление называетсяразложением функции по m переменным .

52)Алгебра логики. Разложение Рида

Алгебра логики – раздел математической логики, в котором изучаются логические операции над высказываниями. Высказывания могут быть истинными, ложными или содержащими истину и ложь в разных соотношениях.

Как известно, если X * Y = 0 то X + Y = X (+) Y

-----------------------------

X Y X*Y X+Y X(+)Y

-----------------------------

0 0 0 0 0

0 1 0 1 1

1 0 0 1 1

-----------------------------

1 1 1 1 0

-----------------------------

Рассмотрим Разложение Шеннона:

F = Xp * G0 + Xp * G1

(Xp * G0) * (Xp * G1) = (Xp * Xp) * (G0 * G1) = 0 * G0 * G1 = 0

Таким образом мы можем заменить в разложении Шеннона OR на XOR:

_

F = Xp * G0 (+) Xp * G1 = (1 (+) Xp) * G0 (+) Xp * G1 = G0 (+) Xp * G0 (+) Xp * G1 =

=G0 (+) (G0 (+)G1) *Xp

Это называется разложением Рида.