
2 практика
.pdfМинистерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра комплексной информационной безопасности электронно-
вычислительных систем (КИБЭВС)
АЛГОРИТМИЧЕСКАЯ СЛОЖНОСТЬ Отчет по практической работе №2
по дисциплине «Структуры данных»
Студент гр. 711-2
_______ Е. П. Толстолес
_______
Принял:
преподаватель КИБЭВС
_______ Н.С. Репьюк
_______
Томск 2022
СОДЕРЖАНИЕ
1Введение…………………………………………………………………………....3
2Ход работы………………………………………………………………………….4
2.1Программа для генерации массивов заданной длинны…………………….4
2.2Сортировка расчёской……………………………………………………….4
2.3Быстрая сортировка………………………………………………………….6
2.4Сортировка методом Шелла………………………………………………...8
2.5Алгоритмическая сложность………………………………………………..9
3Заключение……………………………………………………………………..…11
Приложение А………………………………………………………………………12
2
1 Введение
Целью работы является разработка программы для генерации массивов заданной длинны. Сортировка этих массивов с помощью предыдущих сортировок и оценка алгоритмической сложности каждой сортировки.
3
2Ход работы
2.1Программа для генерации массивов заданной длинны:
На рисунке 2.1 представлен результат работы программы.
Рисунок 2.1 – Работа программы по генерации массива.
Листинг программы представлен в приложении А.
2.2 Сортировка расчёской:
На рисунке 2.2 представлен график зависимости t от n, где n –
количество элементов в массиве, t – время выполнении программы.
4
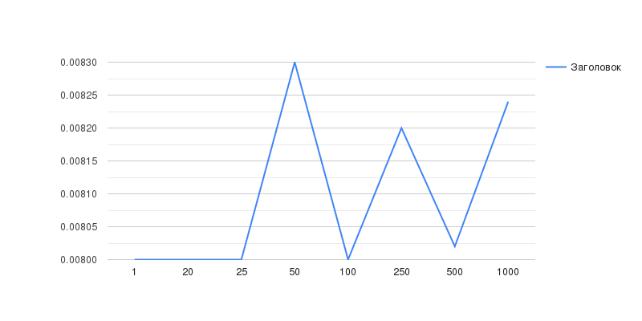
Рисунок 2.2 – График зависимости n от t.
Таблица 2.1 – Таблица значений n и t.
n |
1 |
20 |
25 |
50 |
100 |
250 |
500 |
1000 |
|
|
|
|
|
|
|
|
|
t |
0.008 |
0.008 |
0.008 |
0.0083 |
0.008 |
0.0082 |
0.008 |
0.00824 |
|
|
|
|
|
|
|
|
|
5

На рисунке 2.3 представлен график зависимости n от c, где c -
количество операций, n – размер массива.
Рисунок 2.3 – График зависимости n от c.
Таблица 2.2 – Таблица значений с и n.
n |
|
1 |
20 |
|
25 |
50 |
|
100 |
|
250 |
500 |
|
1000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
1 |
185 |
|
254 |
675 |
|
1629 |
|
5089 |
11965 |
|
27337 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2.3 Быстрая сортировка: |
|
|
|
|
||||||
|
На рисунке 2.4 |
представлен |
график |
зависимости t |
от n, где n – |
|||||||||
количество элементов |
в массиве, t – время выполнении программы. |
|||||||||||||
6

Рисунок 2.4 – График зависимости n от t.
Таблица 2.3 – Таблица значений n и t.
n |
1 |
20 |
25 |
50 |
100 |
250 |
500 |
1000 |
|
|
|
|
|
|
|
|
|
t |
0.0085 |
0.0083 |
0.0082 |
0.0084 |
0.0082 |
0.0082 |
0.0082 |
0.0086 |
|
|
|
|
|
|
|
|
|
На рисунке 2.5 представлен график зависимости n от c, где c -
количество операций, n – размер массива.
Рисунок 2.5 - График зависимости n от c.
7

Таблица 2.4 – Таблица значений с и n.
n |
1 |
20 |
25 |
50 |
100 |
250 |
500 |
1000 |
|
|
|
|
|
|
|
|
|
c |
0 |
126 |
172 |
633 |
2648 |
16011 |
62463 |
250281 |
|
|
|
|
|
|
|
|
|
2.4 Сортировка методом Шелла:
На рисунке 2.6 представлен график зависимости t от n, где n –
количество элементов в массиве, t – время выполнении программы.
Рисунок 2.6 – График зависимости n от t.
Таблица 2.5 – Таблица значений n и t.
n |
1 |
20 |
25 |
50 |
100 |
250 |
500 |
1000 |
|
|
|
|
|
|
|
|
|
t |
0.0079 |
0.008 |
0.008 |
0.008 |
0.0079 |
0.008 |
0.0086 |
0.0082 |
|
|
|
|
|
|
|
|
|
На рисунке 2.7 представлен график зависимости n от c, где c - количество
операций, n – размер массива.
8

Рисунок 2.7 - График зависимости n от c
Таблица 2.6 – Таблица значений с и n.
n |
1 |
20 |
25 |
50 |
100 |
250 |
500 |
1000 |
|
|
|
|
|
|
|
|
|
c |
0 |
83 |
124 |
325 |
850 |
2753 |
6620 |
14484 |
|
|
|
|
|
|
|
|
|
2.5Оценка алгоритмической сложности:
Сортировка выбором для массива из n элементов имеет время выполнения в худшем, среднем и лучшем случае O(n2), предполагая, что сравнения делаются за постоянное время.
При использовании метода сортировки расчёской сложность алгоритма равняется O(n*log2n).
А сортировка методом Шелла имеет такую же сложность, как и пузырьковая сортировка, то есть O(n2).
В теории, быстрая сортировка должна получиться самой скоростной и самой простой по количеству перемещений и сочетаний, по факту самой быстрой оказалась сортировка методом Шелла.
9
Таблица 2.7 – Результаты для худшего и лучшего варианта сортировки.
|
Расчёска |
Быстрая |
Шелла |
|
|
|
|
n |
100 |
100 |
100 |
|
|
|
|
t лучшее |
0.008 |
0.0082 |
0.0078 |
|
|
|
|
t худшее |
0.0085 |
0.0089 |
0.0082 |
|
|
|
|
c лучшее |
1600 |
2630 |
840 |
|
|
|
|
c худшее |
1824 |
3258 |
978 |
|
|
|
|
10
