Бакалавры экономики / Линейная алгебра / 14_Компьютерный практикум по высшей математике в Excel

6.3. Асимптотические формулы Муавра-Лапласа

Пример 2.5 [2,c.73]. В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 семей 300 имеют холодильники.

Решение. Проведем необходимые вычисления в Excel (рис. 6.2).

Рис. 6.2. Применение локальной теоремы Муавра-Лапласа Опишем кратко шаги решения задачи.

Введите данные в ячейки C1, E1 и G1.

Вячейку G3 введите формулу: =(G1-C1*E1)/КОРЕНЬ(C1*E1*(1-E1)).

Вячейку G4 введите формулу: =НОРМРАСП(G3;0;1;0).

Вячейку G5 введите формулу: =G4/КОРЕНЬ(C1*E1*(1-E1)).

Функции НОРМРАСП (x; среднее; стандартное_откл; интегральная) и КОРЕНЬ (число) можно ввести с клавиатуры или вызвать с помощью Мастера функций, выбрав соответственно категорию Статистические или

Математические.

Пример 2.6 [3,c.75]. По данным примера 2.5 вычислить вероятность того, что от 300 до 360 (включительно) семей из 400 имеют холодильники.

Решение. Проведем необходимые вычисления в Excel (рис. 6.3). Опишем шаги решения задачи.

Введите данные в ячейки C1, E1,G1 и I1.

Вячейку G5 введите формулу: =(I1-C1*E1)/КОРЕНЬ(C1*E1*(1-E1)).

Вячейку J5 введите формулу: =(G1-C1*E1)/КОРЕНЬ(C1*E1*(1-E1)).

Вячейку G4 введите формулу: =2*НОРМСТРАСП(G5)-1.

Вячейку J4 введите формулу: =2*НОРМСТРАСП(J5)-1.

Вячейку B5 введите формулу: =(1/2)*(G4-J4).

Функцию НОРМСТРАСП (x) можно ввести с клавиатуры или вызвать с помощью Мастера функций, выбрав категорию Статистические.

50

Рис. 6.3. Применение интегральной теоремы Муавра-Лапласа

6.4. Дискретные случайные величины и их характеристики

Примеры 3.5 и 3.8. [2,c.95, с.100]. Вычислить M(X) и M(Y), D(X) и D(Y)

в задаче о стрелках.

Решение. С помощью Excel несложно организовать решение задачи с получением всех промежуточных результатов вычислений, и построением чертежа, содержащего полигоны распределений вероятностей (рис. 6.4).

Рис. 6.4. Вычисление математического ожидания и дисперсии дискретной случайной величины

51

Опишем кратко шаги решения задачи.

Введите исходные данные в ячейки B3:L4, B6:L7.

Вячейку C9 введите формулу: =СУММПРОИЗВ(B3:L3;B4:L4)

(рис. 6.5).

Вячейку F9 введите формулу: =СУММПРОИЗВ(B6:L6;B7:L7).

Вячейку B11 введите формулу: =(B3-$C9)*(B3-$C9). Скопируйте эту

формулу в ячейки C11:L11.

Вячейку B12 введите формулу: =(B6-$F9)*(B6-$F9). Скопируйте эту формулу в ячейки C12:L12.

Вячейку I9 введите формулу: =СУММПРОИЗВ(B11:L11;B4:L4).

Вячейку L9 введите формулу: =СУММПРОИЗВ(B12:L12;B7:L7).

Функцию СУММПРОИЗВ (массив1; массив2; массив3;…), которая возвращает сумму произведений соответствующих элементов массивов или диапазонов, можно ввести с клавиатуры или вызвать с помощью Мастера функций, выбрав категорию Математические (более подробно о работе с этой функцией написано в разделе 3.2).

52

7.Математическая статистика

Сбольшой эффективностью возможно применение электронных таблиц для решения задач математической статистики.

7.1. Вариационные ряды и их характеристики

Пример 8.1, 8.2 и 8.8 [2,c.264-265, с. 267-269, с.280]. При обследовании выработки 1000 рабочих цеха в отчетном году по сравнению с предыдущим по схеме собственно-случайной выборки было отобрано 100 рабочих. Полученные данные представлены в таблице 7.1.

рабочих)

Необходимо:

а) вычислить среднюю арифметическую и дисперсию распределения рабочих по выработке;

б) построить кумуляту.

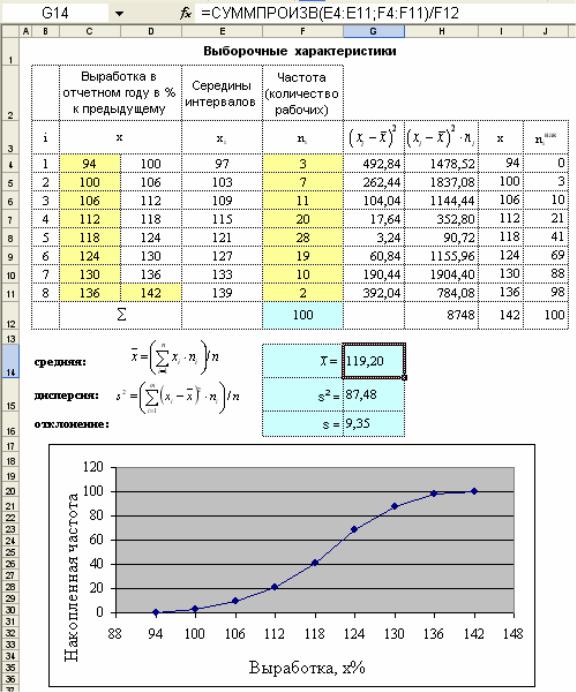
Решение. С помощью Excel несложно организовать вычисление выборочных характеристик интервального вариационного ряда и построить его кумулятивную кривую (рис. 7.1).

Опишем кратко шаги решения задачи. Введите данные в ячейки C4:C11,D11,F4:F11.

Вячейку D4 введите формулу: =C4. Скопируйте эту формулу в ячейки

D5:D10.

Вячейку E4 введите формулу: =(C4+D4)/2. Скопируйте эту формулу в

ячейки E5:E11.

Вячейку F12 введите формулу: =СУММ(F4:F11).

Вячейку G14 введите формулу:

=СУММПРОИЗВ(E4:E11;F4:F11)/F12.

Вячейку G4 введите формулу: =(E4-G$14)*(E4-G$14). Скопируйте эту формулу в ячейки G5:G11.

Вячейку H4 введите формулу: =G4*F4. Скопируйте эту формулу в ячейки H5:H11.

Вячейку H12 введите формулу: =СУММ(H4:H11).

Вячейку G15 введите формулу: =H12/F12.

Вячейку G16 введите формулу: =КОРЕНЬ(G15).

53

Функции СУММ (число1; число2; …), СУММПРОИЗВ(массив1; массив2; …) и КОРЕНЬ (число) можно ввести с клавиатуры или вызвать с помощью Мастера функций, выбрав категорию Математические.

Рис. 7.1. Вычисление выборочных характеристик интервального вариационного ряда и его кумулята

Для построения кумулятивной кривой необходимо сначала с помощью ряда данных частот построить ряд накопленных частот. Для этого в ячейку J4 введите число 0, в ячейку J5 – формулу: =F4, в ячейку J6 – формулу: =F5+J5. Скопируйте эту формулу в ячейки J6:J12.

Далее воспользуйтесь мастером диаграмм.

54

7.2. Формула доверительной вероятности

Пример 9.10 и 9.12 [2,c.314, с.317]. При обследовании выработки 1000 рабочих цеха в отчетном году по сравнению с предыдущим по схеме собственно-случайной выборки было отобрано 100 рабочих. Полученные данные представлены в таблице 7.1. Необходимо определить:

а) вероятность того, что средняя выработка рабочих цеха отличается от средней выборочной не более чем на 1% (по абсолютной величине);

б) границы, в которых с вероятностью 0,9545 заключена средняя выработка рабочих цеха. Рассмотреть случаи повторной и бесповторной выборки;

в) объем выборки, при котором с вероятностью 0,9973 отклонение средней выработки рабочих в выборке от средней выработки всех рабочих цеха не превзойдет 1% (по абсолютной величине).

Решение. Рассмотрим документы Excel, позволяющие для заданной выборки данных в соответствии с расчетными формулами решить любую из 6 типов задач на применение формулы доверительной вероятности при оценке генеральной средней (рисунки 7.2-7.4).

Рис. 7.2. Нахождение доверительной вероятности для оценки генеральной средней

Выполните следующие шаги решения задачи. Введите данные в ячейки C2:C4,K2:K3,H6.

Вячейку E7 введите формулу: =КОРЕНЬ(C3/K3).

Вячейку E9 введите формулу: =КОРЕНЬ((C3/K3)*(1-K3/K2)).

Вячейку H7 введите формулу: =ОКРУГЛ(H6/E7;2).

Вячейку H9 введите формулу: =ОКРУГЛ(H6/E9;2).

Вячейку K7 введите формулу: =2*НОРМСТРАСП(H7)-1. Скопируйте

эту формулу в ячейку K9.

Функции КОРЕНЬ (число), ОКРУГЛ(число; число разрядов) и НОРМСТРАСП(z) можно ввести с клавиатуры или с помощью Мастера функций, выбрав категорию Математические или Статистические.

55

Рис. 7.3. Нахождение доверительного интервала при оценке генеральной средней

Опишем шаги решения задачи.

Введите доверительную вероятность в ячейку C11.

Вячейку E11 введите формулу: =НОРМСТОБР((1+C11)/2).

Вячейки I11 и I13 введите соответственно формулы: =E11*E7 и =E11*E9.

Вячейки K11 и M11 введите соответственно формулы: =C2-I11 и =C2+I11.

Вячейки K13 и M13 введите соответственно формулы: =C2-I13 и =C2+I13.

Функцию НОРМСТОБР(вероятность) можно ввести с клавиатуры или вызвать с помощью Мастера функций, выбрав категорию Статистические.

Рис. 7.3. Нахождение объема выборки при оценке генеральной средней

Выполните следующие шаги решения задачи.

Введите доверительную вероятность в ячейку C16 и предельную ошибку

вячейку J16.

Вячейку E16 введите формулу: =НОРМСТОБР((1+C16)/2).

Вячейку E18 введите формулу: =(E16*E16*C3)/(J16*J16).

Вячейку E20 введите формулу:

=(K2*E16*E16*C3)/(E16*E16*C3+K2*J16*J16).

Вячейку I20 введите формулу: =(E18*K2)/(E18+K2).

56

Пример 9.11 и 9.13 [2,c.315, с.318]. Из партии, содержащей 2000

деталей, для проверки по схеме собственно-случайной выборки было отобрано 200 деталей, среди которых оказалось 184 стандартных. Найти:

а) вероятность того, что доля нестандартных деталей во всей партии отличается от полученной доли в выборке не более чем на 0,02 (по абсолютной величине);

б) границы, в которых с надежностью 0,95 заключена доля нестандартных деталей во всей партии;

в) число деталей, которые надо отобрать в выборку, чтобы с вероятностью 0,95 доля нестандартных деталей в выборке отличалась от генеральной доли не более чем на 0,04 (по абсолютной величине). Найти то же число, если о доле нестандартных деталей, даже приблизительно, ничего неизвестно.

Решение. Рассмотрим документы Excel, позволяющие для заданной выборки данных в соответствии с расчетными формулами решить любую из 6 типов задач на применение формулы доверительной вероятности при оценке генеральной доли (рисунки 7.5-7.7).

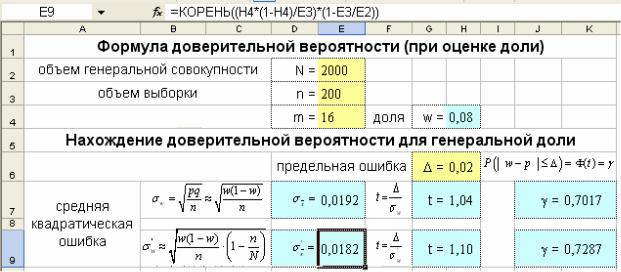
Рис. 7.5. Нахождение доверительной вероятности для оценки генеральной доли

Выполните следующие шаги решения задачи. Введите данные в ячейки E2:E4,H6.

Вячейку H7 введите формулу: =E4/E3.

Вячейку E7 введите формулу: =КОРЕНЬ(H4*(1-H4)/E3).

Вячейку E9 введите формулу: =КОРЕНЬ((H4*(1-H4)/E3)*(1-E3/E2)).

Вячейку H7 введите формулу: =ОКРУГЛ(H6/E7;2).

Вячейку H9 введите формулу: =ОКРУГЛ(H6/E9;2).

Вячейку K7 введите формулу: =2*НОРМСТРАСП(H7)-1. Скопируйте

эту формулу в ячейку K9.

57

Рис. 7.6. Нахождение доверительного интервала при оценке генеральной доли

Опишем шаги решения задачи.

Введите доверительную вероятность в ячейку C11.

Вячейку E11 введите формулу: =НОРМСТОБР((1+C11)/2).

Вячейки I11 и I13 введите соответственно формулы: =E11*E7 и =E11*E9.

Вячейки K11 и M11 введите соответственно формулы: =H4-I11 и =H4+I11.

Вячейки K13 и M13 введите соответственно формулы: =H4-I13 и =H4+I13.

Функцию НОРМСТОБР(вероятность) можно ввести с клавиатуры или вызвать с помощью Мастера функций, выбрав категорию Статистические.

Рис. 7.7. Нахождение объема выборки при оценке генеральной доли

Выполните следующие шаги решения задачи.

Введите доверительную вероятность в ячейку C16 и предельную ошибку

вячейку J16.

Вячейку E16 введите формулу: =НОРМСТОБР((1+C16)/2).

Вячейку E18 введите формулу: (E16*E16*H4*(1-H4))/(J16*J16).

Вячейку E20 введите формулу:

=(E2*E16*E16*H4*(1-H4))/(E16*E16*H4*(1-H4)+E2*J16*J16).

Вячейку I20 введите формулу: =(E18*E2)/(E18+E2).

Вячейку E22 введите формулу:

=(E2*E16*E16*C22)/(E16*E16*C22+E2*J16*J16).

58

7.3. Проверка гипотезы о виде закона распределения

Пример 10.12 [2,c.362-364]. Для эмпирического распределения рабочих цеха по выработке по данным таблицы 7.1 подобрать соответствующее теоретическое распределение и на уровне значимости α=0,05 проверить гипотезу о согласованности двух распределений с помощью критерия 2.

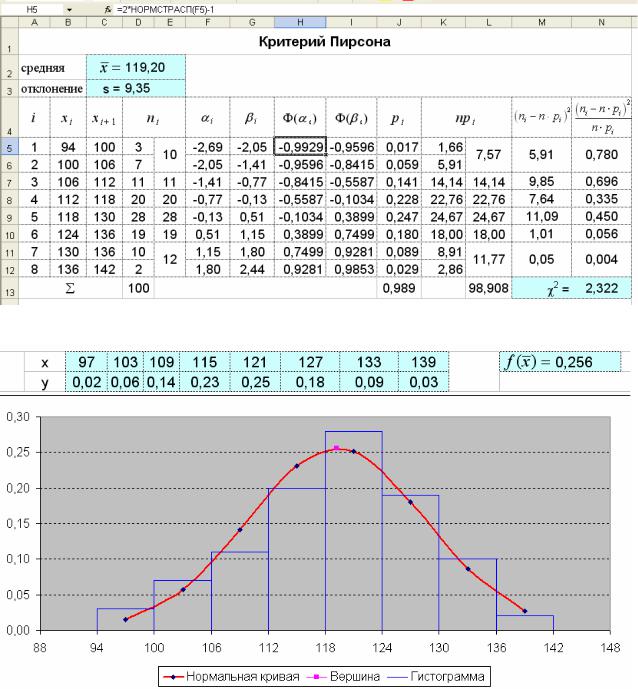
Решение. По виду гистограммы эмпирического распределения можно предположить нормальный закон распределения (рис. 7.9). Проводим в Excel вычисление статистики 2 (рис. 7.8).

Рис. 7.8. Вычисление статистики 2

Рис. 7.9. Гистограмма эмпирического распределения и нормальная кривая

59