Тема 6. Функции нескольких переменных

36. Функции нескольких переменных. Частные производные (определение). Экстремум функции нескольких переменных и его необходимые условия

,- функция двух переменных;

,- функция трех переменных;

,- функцияnпеременных.

Определение 1. Если функциязадана аналитически (т.е. с помощью какой-либо формулы), тообластью определения функции считают множествовсех точек пространства, при которых формула имеет смысл.

Далее рассмотрим функцию двух переменных .

- исходная точка;

-полное приращение аргумента;

- точка приращения;

- значение функции в исходной точке;

- значение функции в точке приращения;

-полное приращение функции n переменныхв точке , соответствующее приращению .

-частное приращение функции по переменнойx;

-частное приращение функции по переменнойy.

Определение 2. Пусть функцияопределена в некоторой окрестности точки.Частной производной функции f в точке по переменнойxназывается предел, если он существует и конечен.

Определение 3. Пусть функцияопределена в некоторой окрестности точки.Частной производной функции f в точке по переменнойyназывается предел, если он существует и конечен.

Заметим, что отношение фактически является функцией одной переменной(отношениетакже является функцией одной переменной). На этом основано следующее правило.

Правило. При вычислении частной производной функции нескольких переменных по некоторой переменной остальные переменные считаем постоянными и вычисление проводим по правилам дифференцирования функции одной переменной.

Определение 4. Точка называетсяточкой максимума функции, если существует такая окрестность , что для всех выполняется неравенство .

Определение 5. Точка называетсяточкой минимума функции, если существует такая окрестность , что для всех выполняется неравенство .

Определение 6. Точки минимума и максимума функцииfназываютсяточками экстремума функцииf. Значение функции в точке экстремума называетсяэкстремумомфункции.

Теорема 1. Если точка является точкой экстремума функции,определенной в некоторой окрестноститочки ,то частные производные функции f в точке не существуют либо равны0 .

Доказательство. Это непосредственно следует из необходимого условия экстремума функции одной переменной, примененного к функциям, получающимся из функциипри фиксации всех переменных, кроме одной, в окрестности , на которую указано в определении точки экстремума.

37. Понятие об эмпирических формулах и методе наименьших квадратов. Подбор параметров линейной функции (вывод системы нормальных уравнений)

На практике часто зависимость между двумя величинами выражается в виде таблицы, полученной опытным путем, в результате наблюдений или статистической обработки:

x	x1	x2	…	xi	…	xn
y	y1	y2	…	yi	…	yn

Во многих случаях удобно представить зависимость между этими величинами с помощью формулы.

Формулы, служащие для аналитического представления опытных данных, получили название эмпирических формул.

Нахождение эмпирических формул

1. установление вида зависимости y=f(x) (линейная, квадратичная, степенная, показательная, логарифмическая);

2. определение неизвестных параметров функции.

Наиболее часто для нахождения неизвестных параметров применяется метод наименьших квадратов, заключающийся в том, что бы было минимальным выражение

.

Рассмотрим случай, когда зависимость является линейной, т.е. y=f(x) есть линейная функцияy=ax+bс неизвестными параметрамиa,b.

Для этого необходимо найти наименьшее значение функции двух переменных

.

По необходимому условию экстремума функции двух переменных

, т.е.,

или .

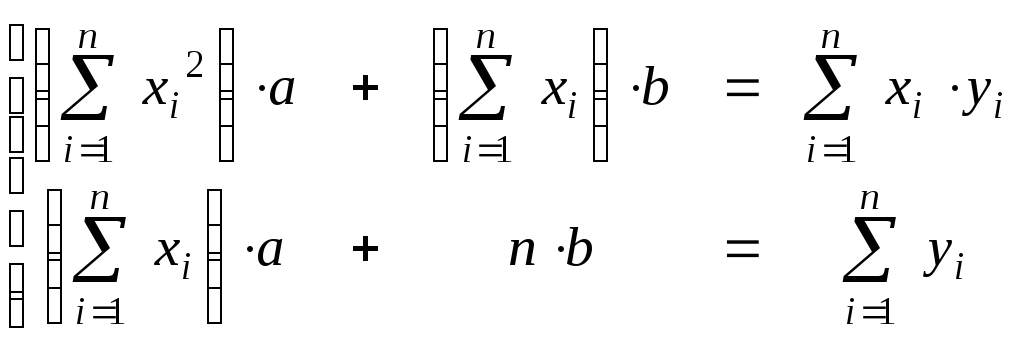Эта система называется системой нормальных уравнений.

Определитель этой системы >0. Это можно доказать методом математической индукции. Следовательно, система имеет единственное решение.

Также можно доказать, что это решение является точкой минимума функции S(a,b).