35. Знакопеременные ряды. Абсолютная и условная сходимость рядов

Определение 1. Если сходится ряд , то рядназываетсяабсолютно сходящимся.

Теорема 1. Если сходится ряд , то ряд также сходится.

Например, ряд является абсолютно сходящимися, так как ряд сходится по признаку сравнения, ибо для любогоnN,а ряд сходится (a=2>1) .

Абсолютно сходящиеся ряды имеют ряд важных свойств, которыми обладают конечные суммы чисел:

- слагаемые можно переставлять местами;

- слагаемые можно группировать разными способами;

- суммы рядов можно перемножать.

Определение 2. Ряд называетсяперестановкой ряда ,если существует биекция такая, чтодля любогоnN .

Теорема 2. Если ряд абсолютно сходится, то сходится, и притом абсолютно, любая перестановка данного ряда, и их суммы совпадают.

Определение 3. Если ряд сходится, а ряд расходится, то ряд называетсяусловно сходящимся.

Ряд является условно сходящимся. Действительно, ряд 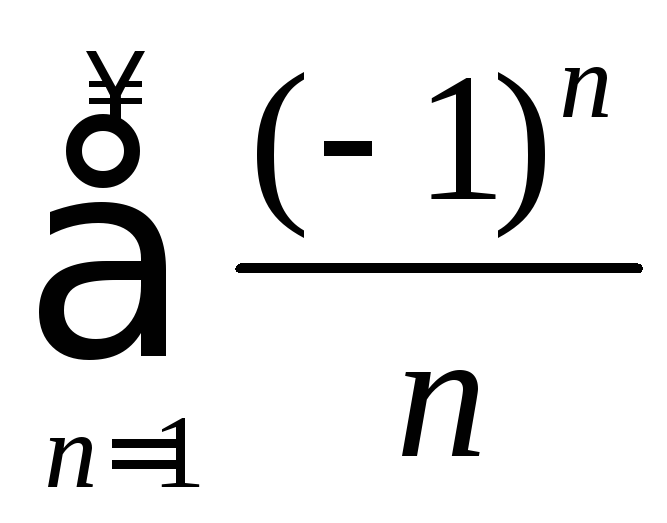сходится (по теореме Лейбница), а ряд расходится.

Теорема 3  (Римана). Если числовой ряд условно сходится,то для любого существует такой числовой ряд,полученный перестановкой членов ряда ,что ряд сходится и его сумма равнаC.