
Teoria_veroyatnostey_15-19
.rtf15. Дисперсия ДСВ и ее св-ва (с выводом). Примеры.
|
Дисперсией D(Х) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
|
Доказательство. С учетом того, что мат ожид М(Х) и квадрат мат-гоожид М2(Х) – величины постоянные, можно записать:
![]()
![]()
![]()
В
качестве характеристики рассеяния
нельзя брать математическое ожидание
отклонения случайной величины от ее
математического ожидания
 ,
ибо согласно свойству 6 математического
ожидания эта величина равна нулю для
любой случайной величины.
,
ибо согласно свойству 6 математического
ожидания эта величина равна нулю для
любой случайной величины.
Выбор
дисперсии, определяемой по формуле, в
качестве характеристики рассеяния
значений случайной величины Х оправдывается
также тем, что, как можно показать,
математическое ожидание квадрата
отклонения случайной величины Х от
постоянной величины С минимально именно
тогда, когда эта постоянная С равна
математическому ожиданию
 ,
т.е.
,
т.е.
 .
.
Если
случайная величина Х - дискретная с
конечным числом значений, то
 (3.11).
(3.11).
Если
случайная величина Х - дискретная с
бесконечным, но счетным множеством
значений, то
 (если ряд в правой части равенства
сходится).
(если ряд в правой части равенства
сходится).
Дисперсия
D(Х)
имеет размерность квадрата случайной
величины, что не всегда удобно. Поэтому
в качестве показателя рассеяния
используют также величину
 .
.
|
Средним
квадратическим отклонением (стандартным
отклонением или стандартом)
|
Свойства дисперсии случайной величины.
-
Дисперсия постоянной величины равна нулю:
 .
.
□
 .
■
.
■
2.
Постоянный множитель можно выносить
за знак дисперсии, возведя его при этом
в квадрат:
 .
.
□ Учитывая
свойство 2 математического ожидания,
получим
 .
■
.
■
3.
Дисперсия случайной величины равна
разности между математическим ожиданием
квадрата случайной величины и квадратом
ее математического ожидания:
 (3.16)
или
(3.16)
или
 где
где
 .
.
□ Пусть М(Х) = а. Тогда D(Х) = М(Х - а)2 = М(Х2 - 2аХ + а2). Учитывая, что а - величина постоянная, неслучайная, найдем
D(Х) = М(Х)2 - 2аМ(Х) + а2 = М(Х2) - 2а·а + а2 = M(X2) - a2.
Это свойство часто используют при вычислении дисперсии. Вычисление по формуле (3.16) дает, например, упрощение расчетов по сравнению с основной формулой (3.11), если значения xi случайной величины - целые, а математическое ожидание, а значит, и разности (xi - а) - нецелые числа.
4.
Дисперсия алгебраической суммы конечного
числа независимых случайных величин
равна сумме их дисперсий:
 .
.
□ По
свойству 3:
 .
Обозначая
.
Обозначая
 ,
,
 и учитывая, что для независимых случайных
величин М(ХУ)=М(Х)М(У), получим
и учитывая, что для независимых случайных
величин М(ХУ)=М(Х)М(У), получим
 .■
.■
Обращаем
внимание на то, что дисперсия как суммы,
так и разности независимых случайных
величин Х и У равна сумме их дисперсий,
т.е.
 .
.
3амечание.
Обратим внимание на интерпретацию
математического ожидания и дисперсии
в финансовом
анализе.
Пусть, например, известно распределение
доходности Х некоторого актива (например,
акции), т.е. известны значения доходности
xi
и соответствующие их вероятности pi
за рассматриваемый промежуток времени.
Тогда, очевидно, математическое ожидание
М(Х) выражает среднюю (прогнозную)
доходность актива, а дисперсия D(X) или
среднее квадратическое отклонение
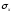 - меру отклонения, колеблемости доходности
от ожидаемого среднего значения, т.е.
риск данного актива.
- меру отклонения, колеблемости доходности
от ожидаемого среднего значения, т.е.
риск данного актива.
Математическое ожидание, дисперсия, среднее квадратическое отклонение и другие числа, призванные в сжатой форме выразить наиболее существенные черты распределения, называются числовыми характеристиками случайной величины.
Обращаем внимание на то, что сама величина Х - случайная, а ее числовые характеристики являются величинами неслучайными, постоянными.
16. Мат. ожидание и дисперсия числа и частости наступлений события в повторных независимых испытаниях (с выводом).
Математическое
ожидание частости события в n независимых испытаниях, в
каждом из которых оно может наступить
с одной и той же вероятностью р, равно
р, т.е.
события в n независимых испытаниях, в
каждом из которых оно может наступить
с одной и той же вероятностью р, равно
р, т.е.
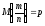 а ее дисперсия
а ее дисперсия
 .
.
□ Частость
события
 есть
есть
 ,
т.е.
,
т.е.
 ,
где Х - случайная величина, распределенная
по биномиальному закону. Поэтому
,
где Х - случайная величина, распределенная
по биномиальному закону. Поэтому
 .
.
 ■
■
Теорема. Сл\в Х=m, распределённую по биномиальному закону, можно интерпретировать как число m объектов, обладающих данным св-м, из общего числа n объектов, случайно извлечённых из некоторой воображаемой бесконечной совокупности, доля p объектов которой обладает этим св-м. Поэтому рапределение можно расм-ть как модификацию биномиального распр-я для случая конечной совокупности, состоящей из N объектов, М из кот обладают этим св-м.
17. СВ, распределенная по биномиальному закону. Ее мат. ожидание и дисперсия. Закон распределения Пуассона.
Дискретная случайная величина Х имеет биномиальный закон распределения с параметрами npq, если она принимает значения 0, 1, 2,..., m,... ,n с вероятностями
 ,
,
где 0<р<l, q=1-p.
Как видим, вероятности Р(Х=m) находятся по формуле Бернулли, следовательно, биномиальный закон распределения представляет собой закон распределения числа Х=m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.
Ряд распределения биномиального закона имеет вид:

Очевидно,
что определение биномиального закона
корректно, т.к. основное свойство ряда
распределения
 выполнено, ибо
выполнено, ибо
 есть не что иное, как сумма всех членов
разложения бинома Ньютона:
есть не что иное, как сумма всех членов
разложения бинома Ньютона:
Математическое ожидание случайной величины Х, распределенной по биноминальному закону,
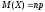 а
ее дисперсия
а
ее дисперсия

Определение.
Дискретная
случайная величина Х имеет закон
распределения Пуассона
с параметром λ
> 0, если
она принимает значения 0, 1, 2,..., m,
... (бесконечное, но счетное множество
значений) с вероятностями 
 ,
,
Ряд распределения закона Пуассона имеет вид:

Очевидно,
что определение закона Пуассона
корректно, так как основное свойство
ряда распределения
 выполнено,
ибо сумма ряда
выполнено,
ибо сумма ряда
 .
.
На рис. 4.1 показан многоугольник (полигон) распределения случайной величины, распределенной по закону Пуассона Р(Х=m)=Рm(λ) с параметрами λ = 0,5, λ = 1, λ = 2, λ = 3,5.
Теорема. Математическое oжидaниe и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона, т.е.
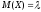 и
и
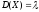
18. Функция распределения СВ, ее определение, свойства и график.
|
Функцией распределения случайной величины Х называется функция F(х), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х:
|
Функцию F(x) иногда называют интегральной функцией распределения или интегральным законом распределения.
Геометрически функция распределения интерпретируется как вероятность того, что случайная точка Х попадет левее за данной точки х.
Функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений. Сумма всех скачков функции F(х) равна 1.
Общие свойства функции распределения.
1.
Функция распределения случайной величины
есть неотрицательная функция, заключенная
между нулем и единицей:
 .
.
Утверждение следует из того, что функция распределения – это вероятность.
-
Функция распределения случайной величины есть неубывающая функция на всей числовой оси.
Пусть
 и
и
 -
точки числовой оси, причем
-
точки числовой оси, причем
 >
> .
Покажем, что
.
Покажем, что
 .
Рассмотрим 2 несовместных события
.
Рассмотрим 2 несовместных события
 ,
,
 .
Тогда
.
Тогда
 .
.
Это
соотношение между событиями легко
усматривается из их геометрической
интерпретации (рис.3.6). По теореме
сложения:
 или
или
 откуда
откуда
 .
.
Так
как вероятность ,
то
,
то
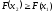 ,
т.е.
,
т.е.
 -
неубывающая функция. ☻
-
неубывающая функция. ☻
-
На минус бесконечности функция распределения равна нулю, на плюс бесконечности равна единице, т.е.

 .
.
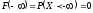 как
вероятность невозможного события
как
вероятность невозможного события
 .
.
 как
вероятность достоверного события
как
вероятность достоверного события
 .
.
-
Вероятность попадания случайной величины в интервал
 (включая
(включая
 )
равна приращению ее функции распределения
на этом интервале, т.е.:
)
равна приращению ее функции распределения
на этом интервале, т.е.:
 .
.
Формула
следует непосредственно из формулы
 .
.
19. Непрерывная СВ. вероятность отдельно взятого значения НСВ. Мат. ожидание и дисперсия НСВ.
|
Случайная величина Х называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек (точки излома). |
На
рис. 3.7 показана Функция распределения
непрерывной случайной величины Х,
дифференцируемая во всех точках, кроме
трех точек излома.
Теорема. Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю.
☺ Покажем,
что для любого значения
 случайной величины Х вероятность
случайной величины Х вероятность
 .
Представим
.
Представим
 в виде
в виде
 .
.
Применяя
свойство
 функции распределения случайной величины
Х и учитывая непрерывность F(x),
получим:
функции распределения случайной величины
Х и учитывая непрерывность F(x),
получим:
 .
☻
.
☻
Из
приведенной выше теоремы следует, что
нулевой вероятностью могут обладать и
возможные события, так как событие,
состоящее в том, что случайная величина
Х приняла конкретное значение
 ,
является возможным.
,
является возможным.
Следствие.
Если Х - непрерывная случайная величина,
то вероятность попадания случайной
величины в интервал
 не зависит от того, является этот интервал
открытым или закрытым, т.е.
не зависит от того, является этот интервал
открытым или закрытым, т.е.
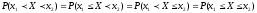 .
.
Математическим
ожиданием непрерывной случайной
величиныХ,
возможные значения которой принадлежат
отрезку [a,b], называется определенный
интеграл
 .
Если возможные значения случайной
величины рассматриваются на всей
числовой оси, то математическое ожидание
находится по формуле:
.
Если возможные значения случайной
величины рассматриваются на всей
числовой оси, то математическое ожидание
находится по формуле: .
При этом предполагается, что интеграл
абсолютно сходится.
.
При этом предполагается, что интеграл
абсолютно сходится.
Дисперсией
непрерывной случайной величины
называется математическое ожидание
квадрата ее отклонения.
 .
.
По
аналогии с дисперсией дискретной
случайной величины, для
практического вычисления дисперсии
используется формула:
 .
.
