Данные обследования населения поселка в возрасте 20–40 лет

В графах «Обр.» (образование): в – высшее, с-с – среднее специальное, с – среднее; «Возр.» – возраст; «Дох.» – средний месячный доход, тыс. руб.

№	Пол	Обр.	Возр.	Дох.
22	ж	в	38	15,4
15	ж	в	23	15,8
24	ж	в	24	16,2
33	м	в	33	16,2
36	ж	в	34	16,2
13	ж	в	40	16,4
10	ж	в	26	16,5
19	м	в	33	17,3
17	м	в	27	17,8
38	ж	в	28	18,3
35	м	в	27	18,4
8	ж	в	28	19,6
28	ж	в	32	21,4
3	ж	в	21	23,4
5	ж	в	25	24,2
9	м	с	24	16,2
37	м	с	24	16,7
25	м	с	33	18,9
31	м	с	29	19,6
6	м	с	29	23,7
32	ж	с-с	28	15,1
16	ж	с-с	21	15,9
18	ж	с-с	25	15,9
23	м	с-с	30	15,9
14	м	с-с	40	16,0
21	ж	с-с	22	16,6
30	ж	с-с	31	16,7
29	ж	с-с	20	16,8
34	ж	с-с	23	16,8
27	м	с-с	29	16,9
20	ж	с-с	35	17,4
11	м	с-с	38	17,4
12	ж	с-с	33	17,6
4	м	с-с	20	17,7
40	ж	с-с	22	18,1
39	м	с-с	35	19,6
2	ж	с-с	39	19,6
26	ж	с-с	22	23,6
1	м	с-с	37	23,8
7	ж	с-с	36	24,9

На основании данных обследования жителей поселка:

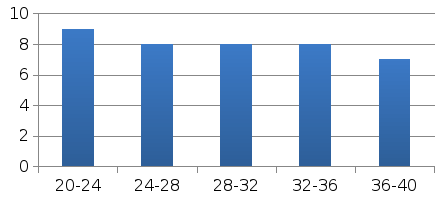
1. Провести группировку жителей по возрасту на 5 групп с равными интервалами и представить полученные данные в виде статистического ряда распределения. На основе полученного ряда построить гистограмму, полигон и кумуляту распределения жителей по возрасту.

2. Составить и назвать статистическую таблицу с монографическим подлежащим и сложным сказуемым, построенным по количественному и атрибутивному признакам. Количество групп в сказуемом – оптимальное, каждая содержит по 2 подгруппы.

3. Сгруппировать жителей поселка: а) по доходу на 7 группы с равными интервалами; б) по возрасту на 4 группы с равными интервалами. Для каждой группировки определить относительные показатели структуры. Для первой группировки найти средний возраст жителей каждой группы, для второй – их средний доход.

4. Исчислить по сгруппированным выше данным (пункт 3а) средний доход жителей с помощью следующих средних (простых и взвешенных): а) арифметической; б) гармонической.

5. Рассчитать показатели вариации возраста жителей: а) по сгруппированным выше (пункт 3б) данным с использованием средней арифметической простой и взвешенной; б) по не сгруппированным данным.

6. Определить модальные и медианные значения возраста жителей: а) по не сгруппированным данным; б) из статистического ряда распределения (пункт 1) аналитически и графически.

7. Найти параметры уравнения линейной регрессии для зависимости заработной платы рабочих от их разряда.

Задание 1.

1. Определим величину интервала по формуле:

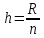
R = X_max – X_min

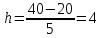
2. Представим полученные данные в виде статистического ряда распределения (см. таблицу 2).

Вариант		Частота			Накопленная частота		Частость
1	20-24	|||||||||||	9	9		22,5
2	24-28	||||||||||	8	17		20
3	28-32	||||||||||	8	25		20
4	32-36	||||||||||	8	33		20
5	36-40	|||||||||	7	40		17,5
ИТОГО		40			-		100

3. На основе полученного ряда построим гистограмму, полигон и кумуляту.