13. Операции над графами: дополнение, объединение и пересечение. Примеры.

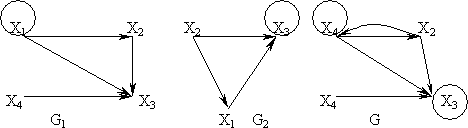
Пересечение (произведение) графовПересечением графов G1(X₁,Г₁X₁) и G2(X₂,Г₂X₂) называется такой граф G(X,ГX), у которого множество вершин есть пересечение множеств вершин графов X=X₁ÇX₂, а отображение есть пересечение отображений перемножаемых графовГX=Г₁X₁ÇГ₂X₂.Пример.Пересечение графов G₁ и G₂ предыдущего примера есть граф G(X,ГX)

Объединение графов.

Объединением графов G₁(X₁,Г₁X₁) и G₂(X₂,Г₂X₂) называется такой граф G(X,ГX), у которого множество вершин есть сумма множеств вершин объединяемых графов X=X₁ÈX₂, а отображение есть сумма отображений объединяемых графов ГX=Г₁X₁ÈГ₂X₂. обозначает: G=G₁ÈG₂.

Пример. Заданы графы G₁ и G₂:

Требуется определить G(X,ГX)=G₁ÈG₂.

    

           

1. Дополнением графа G₁(V₁,E₁) называется граф G₂(V₂,E₂), у которого множество вершин такое же, как у исходного графа, а множество ребер представляет собой дополнение до множества  Вершины графа G₂ смежны только в том случае, когда они не смежны в исходном графе. Обозначение: ` G₁(V₁,E₁). Дополнение графов есть дополнение

Дополнение к полному графу – пустой граф. Другой пример показан на рисунке.

14. Маршруты, циклы и цепи в неориентированных графах. Связность.

Определение 4.9. Последовательность из  ребер графа (не обязательно различных) называется маршрутом длины , если любые два рядом стоящие в этой последовательности ребра смежные. Кроме того, если эти два рядом стоящие ребра ориентированные, то в инцидентную им вершину ребро, стоящее слева, должно входить, а ребро, стоящее справа, из нее выходить.

 Любая вершина, инцидентная двум рядом стоящим ребрам маршрута, называется внутренней или промежуточной вершиной. Так как ребра и вершины в маршруте могут повторяться, то внутренняя вершина может также оказаться начальной или конечной вершиной.

  Маршрут неориентированного графа называют неориентированным маршрутом (составной цепью), а маршрут орграфа называют ориентированным маршрутом (составным путем). Если все ребра незамкнутого маршрута попарно различны, то такой маршрут неориентированного графа называется цепью, а орграфа - путем. Если попарно различны все вершины незамкнутого маршрута, то такой маршрут неориентированного графа называется простой цепью, а орграфа - простым путем. Если попарно различны все ребра замкнутого маршрута, то такой маршрут неориентированного графа называется циклом, а орграфа - контуром. Замкнутый маршрут, в котором попарно различны все вершины, кроме первой и последней, называется в неориентированном графе простым циклом, а в орграфе - простым контуром.

  Маршрут назовем нетривиальным, если он содержит хотя бы одно ребро; для систематичности рассуждений вводится еще нуль-маршрут, вообще не содержащий ребер, - этот маршрут состоит

только из одной вершины графа.

На рис.4.18 приведен пример составной цепи, на рис.4.19 приведен пример пути, а на рис.4.20 - пример простой цепи.