Вариант 7

(для студентов, номера личных дел которых оканчиваются цифрой 7)

Контрольная работа № 1

1. Даны матрицы

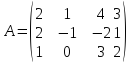и .

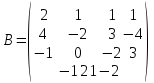Найти ранг матрицы

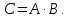
2. Методом обратной матрицы решить систему:

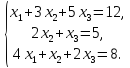
3. Установить, имеет ли однородная система

ненулевое решение. Найти общее решение системы.

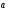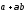4. Найти значение параметра α, при котором векторы иперпендикулярны, есл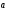и= (6;–3; 5) и 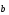= (–1; –3; 2).

5. Даны четыре вектора

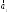=(2;1;0); 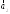=(1;–1;2);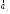=(2;2;–1);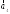=(3;7;– 7)

в некотором базисе. Показать, что векторы 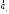,,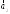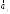образуют базис, и найти координаты вектора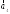в этом базисе.

6. Найти собственные значения и собственные векторы линейного оператора 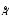, заданного матрицейА= .

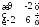7. а) Методом Лагранжа привести квадратичную форму

f(x_1, x₂)=4x₁²+3 x₂²+4x₁x₂

к каноническому виду (указать пример соответствующего преобразования координат).

б) По критерию Сильвестра исследовать на знакоопределенность квадратичную форму

f(x_1, x₂, x₃)= –2x₁²+5x₂²+3x₃² +2x₁x₂–2x₁x₃ –2x₂x_3.

Контрольная работа №2

1. Точк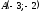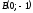и ,и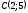являются вершинами треугольникаABC. Определить координаты точки Н – основания медианы АН треугольника АВС и составить уравнение медианы треугольника, опущенной из точки А на сторону ВС. Сделать чертеж.

2. Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс, симметрично относительно начала координат, если уравнения ее асимптот 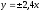, а расстояние между вершинами равно 48.

3. Составить уравнение диаметра окружности 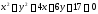, перпендикулярного к прямой.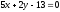

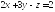4. Написать уравнение плоскости, проходящей через точку и линию пересечения плоскостейи.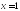

5. Верно ли, что прямая 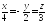параллельна плоскости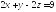? Если да, то найти расстояние между этими прямой и плоскостью.

Вариант 8

(для студентов, номера личных дел которых оканчиваются цифрой 8)

Контрольная работа № 1

1. Даны матрицы

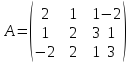и

Определить, имеет ли матрица 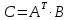обратную.

2. По формулам Крамера решить систему:

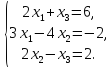
3. Решить систему линейных уравнений:

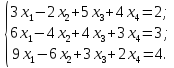
Найти какое-нибудь базисное решение.

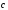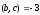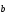4. Найти вектор , коллинеарный вектору=(1; 1; –2) и такой, что , где= (–3; 1; 2).

5. Даны четыре вектора

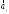=(1;1;1); 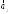=(0;2;3);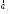=(0;1;5);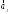=(2; –1;1)

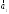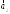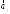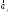в некотором базисе. Показать, что векторы ,,образуют базис, и найти координаты векторав этом базисе.

6.Найти собственные значения и собственные векторы линейного оператора , заданного матрицейА= .

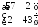7. а) Методом Лагранжа привести квадратичную форму

f(x_1, x₂)=–x₁²+3 x₂²+4x₁x₂

к каноническому виду (указать пример соответствующего преобразования координат).

б) По критерию Сильвестра исследовать на знакоопределенность квадратичную форму

f(x_1, x₂, x₃)=x₁²+ x₂²+ x₃² +4x₁x₂+6x₁x₃ +4x₂x_3..

Контрольная работа №2

1. Вычислить площадь квадрата, если две его стороны лежат на прямых ,.

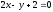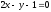2. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, если его большая ось равна 10, а расстояние между фокусами равно 8.

3. Вычислить площадь треугольника, образованного асимптотами гиперболы 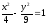и прямой.

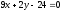4. Написать уравнение плоскости, проходящей через точку параллельно векторами.

5. Написать уравнение плоскости, проходящей через начало координат перпендикулярно прямой, проходящей через точки и.