
- •1.Метод наименьших квадратов: алгоритм метода; условия применения.
- •2.Типы переменных в эконометрических моделях. Структурная и приведённая формы спецификации эконометрических моделей.
- •3. Статистические свойства оценок параметров парной регрессионной модели
- •4. Этапы построения эконометрических моделей.
- •5.Порядок оценивания линейной эконометрической модели из изолированного уравнения в Excel. Смысл выходной статистической информации сервиса Регрессия. (10) стр 41
- •6.Спецификация и оценивание мнк эконометрических моделей нелинейных по параметрам. (30) стр.24-25,
- •7. Классическая парная регресионная модель. Спецификация модели. Теорема Гаусса-Маркова.
- •8. Метод наименьших квадратов: алгоритм метода, условия применения.
- •9.Идентификация отдельных уравнений системы одновременных уравнений: порядковое условие. (30)
- •Необходимое условие идентифицируемости
- •10.Оценка параметров парной регрессионной модели методом наименьших квадратов. (10)
- •11.Фиктивные переменные: определение, назначение, типы.
- •12.Автокорреляция случайного возмущения. Причины. Последствия.
- •13.Алгоритм проверки значимости регрессора в парной регрессионной модели.
- •14.Интервальная оценка ожидаемого значения зависимой переменной в парной регрессионной модели.
- •15. Тест Чоу на наличие структурных изменений в регрессионной модели. (20) стр. 59,60
- •16. Алгоритм проверки адекватности парной регрессионной модели. (20) стр. 37, 79
- •17. Коэффициент детерминации в парной регрессионной модели.
- •18. Оценка параметров множественной регрессионной модели методом наименьших квадратов.
- •20. Гетероскедастичность случайного возмущения. Причины. Последствия. Тест gq(20)
- •21.Фиктивная переменная наклона: назначение; спецификация регрессионной модели с фиктивной переменной наклона; значение параметра при фиктивной переменной. (20) стр.65
- •22..Алгоритм теста Дарбина-Уотсона на наличие (отсутствие) автокорреляции случайных возмущений. (20) стр 33
- •23. Структурная и приведённая формы спецификации эконометрических моделей.
- •24. Гетероскедастичность случайного возмущения. Причины. Последствия. Алгоритм теста Голдфельда-Квандта на наличие или отсутствие гетероскедастичности случайных возмущений.
- •Алгоритм теста Голдфелда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений.
- •25. Спецификация и оценивание мнк эконометрических моделей нелинейных по параметрам.
- •26. Способы корректировки гетероскедастичности. Метод взвешенных наименьших квадратов
- •27.Проблема мультиколлинеарности в моделях множественной регрессии.Признаки мультиколлениарности.
- •28.Что такое логит,тобит,пробит.
- •29. Что такое Метод наибольшего правдоподобия стр. 62.
- •30. Что такое стационарный процесс?
- •31.Свойства временных рядов.
- •32.Модели ar и var .
- •33. Идентифицируемость системы.
- •34. Настройка модели с системой одновременных уравнений.
- •35.Что такое метод Монте-Карло стр 53
- •36.Оценить качество модели по f, gq, dw (линейнные).Стр.33, 28-29
- •37. Оценка погрешностей параметров эконометрической модели методом Монте-Карло .
- •38. Отражение в модели влияния неучтённых факторов. Предпосылки теоремы Гаусса-Маркова.
- •39.Модели временных рядов. Свойства рядов цен акций на бирже (20) с.93.
- •40. Ожидаемое значение случайной переменной, её дисперсия и среднее квадратическое отклонение. (20) с.12-21
- •41. Оценка параметров парной регрессионной модели методом наименьших квадратов с использованием сервиса Поиск решения.
- •42. Проверка статистических гипотез, t-статистика Стьюдента, доверительная вероятность и доверительный интервал, критические значения статистики Стьюдента. Что такое “толстые хвосты”?
- •43.Проблема мультиколлинеарности в моделях множественной регрессии. Признаки мультиколлинеарности
- •44. Частные коэффициенты детерминации.
- •46. Экономический смысл коэффициентов линейного и степенного уравнений регрессии.
- •47.Оценка коэффициентов модели Самуэльсона-Хикса
- •48. Ошибки от включения в модель незначимых переменных или исключения значимых.С.80
- •49. Исследование множественной регрессионной модели с.74-79.
- •50. Мультиколлинеарность: чем плоха, как обнаружить и как бороться.
- •51. Признаки стационарности стохастического процесса. Что такое «Белый шум»? с.100
- •52. Структурная и приведённая формы спецификации эконометрических моделей.
- •53. Алгоритм проверки значимости регрессора в парной регрессионной модели. По t-статистике, по f-статистике.
- •54.Свойства рядов цен на фондовом рынке. Принципы построения портфеля Марковица с.93,102
- •55.Динамическая модель из одновременных линейных уравнений (привести пример) с.105.
- •56. Метод наибольшего правдоподобия: принципы и целесообразность использования
- •57. Этапы исследования модели множественной регрессии с.74-79.
52. Структурная и приведённая формы спецификации эконометрических моделей.
Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные.
Эндогенные
переменные
– это зависимые переменные, число
которых равно числу уравнений в системе
и которые обозначаются через
![]() ,
взаимозависимые переменные, которые
определяются внутри модели (системы).
,
взаимозависимые переменные, которые
определяются внутри модели (системы).
Экзогенные
переменные
– это предопределенные переменные,
влияющие на эндогенные переменные, но
не зависящие от них, независимые
переменные, которые определяются вне
системы.
Обозначаются через
![]() .
.
В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные).
Предопределенными переменными наз. экзогенные и лаговые эндогенные переменные сис-мы.
Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной.
Структурная
форма модели в правой части содержит
при эндогенных переменных коэффициенты
![]() и экзогенных переменных – коэффициенты
и экзогенных переменных – коэффициенты![]() ,
которые называютсяструктурными
коэффициентами
модели. Все переменные в модели выражены
в отклонениях от среднего уровня, т.е.
под
,
которые называютсяструктурными
коэффициентами
модели. Все переменные в модели выражены
в отклонениях от среднего уровня, т.е.
под
![]() подразумевается
подразумевается![]() ,
а под
,
а под![]() – соответственно
– соответственно![]() .
Поэтому свободный член в каждом уравнении
системы отсутствует. (3.3) ниже представлено.
.
Поэтому свободный член в каждом уравнении
системы отсутствует. (3.3) ниже представлено.
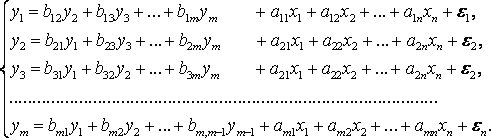
Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.
Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:
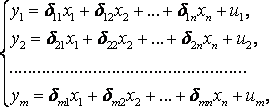 (3.4)
(3.4)
где
![]() – коэффициенты приведенной формы
модели,
– коэффициенты приведенной формы
модели,![]() – остаточная величина для приведенной
формы.
– остаточная величина для приведенной
формы.
По
своему виду приведенная форма модели
ничем не отличается от системы независимых
уравнений, параметры которой оцениваются
традиционным МНК. Применяя МНК, можно
оценить
![]() ,
а затем оценить значения эндогенных
переменных через экзогенные.
,
а затем оценить значения эндогенных
переменных через экзогенные.
Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели.
Структурные модели можно подразделить на три вида: - идентифицируемые;-неидентифиц.;- сверхидентифицируемые.
Условие идентифицируемости модели может быть записано в виде следующего правила:
Предопределённых + 1 = Эндогенных идентифицируемо
Предопределённых + 1 < Эндогенных неидентифицируемо
Предопределённых + 1 > Эндогенных сверхидентифицируемо
53. Алгоритм проверки значимости регрессора в парной регрессионной модели. По t-статистике, по f-статистике.
При проверке качества спецификации парной регрессии наиболее важной является задача установления наличия линейной зависимости между эндогенной переменной и регрессором модели. С этой целью проверяют значимость оценки параметра b (при регрессоре модели).
Алгоритм проверки значимости параметра b выполняется в следующей последовательности:
1) оценка параметров парной регрессии
2) оценка дисперсии возмущений S2
3)
оценка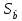 среднего квадратичного отклонения
параметраb
среднего квадратичного отклонения
параметраb
4)
выбор значения tкр
(по заданному уровню значимости
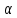 и числу степеней свободы (n-2)
из таблиц распределения Стьюдента)
и числу степеней свободы (n-2)
из таблиц распределения Стьюдента)
5)
проверка неравенства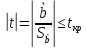 при Н0:b=0
при Н0:b=0
Если данное неравенство выполняется, то регрессор признается незначимым, если не выполняется, то данная гипотеза отвергается и регрессор признается значимым, т.е. между эндогенной переменной и регрессором присутствует линейная зависимость.
