
- •1.Метод наименьших квадратов: алгоритм метода; условия применения.
- •2.Типы переменных в эконометрических моделях. Структурная и приведённая формы спецификации эконометрических моделей.
- •3. Статистические свойства оценок параметров парной регрессионной модели
- •4. Этапы построения эконометрических моделей.
- •5.Порядок оценивания линейной эконометрической модели из изолированного уравнения в Excel. Смысл выходной статистической информации сервиса Регрессия. (10) стр 41
- •6.Спецификация и оценивание мнк эконометрических моделей нелинейных по параметрам. (30) стр.24-25,
- •7. Классическая парная регресионная модель. Спецификация модели. Теорема Гаусса-Маркова.
- •8. Метод наименьших квадратов: алгоритм метода, условия применения.
- •9.Идентификация отдельных уравнений системы одновременных уравнений: порядковое условие. (30)
- •Необходимое условие идентифицируемости
- •10.Оценка параметров парной регрессионной модели методом наименьших квадратов. (10)
- •11.Фиктивные переменные: определение, назначение, типы.
- •12.Автокорреляция случайного возмущения. Причины. Последствия.
- •13.Алгоритм проверки значимости регрессора в парной регрессионной модели.
- •14.Интервальная оценка ожидаемого значения зависимой переменной в парной регрессионной модели.
- •15. Тест Чоу на наличие структурных изменений в регрессионной модели. (20) стр. 59,60
- •16. Алгоритм проверки адекватности парной регрессионной модели. (20) стр. 37, 79
- •17. Коэффициент детерминации в парной регрессионной модели.
- •18. Оценка параметров множественной регрессионной модели методом наименьших квадратов.
- •20. Гетероскедастичность случайного возмущения. Причины. Последствия. Тест gq(20)
- •21.Фиктивная переменная наклона: назначение; спецификация регрессионной модели с фиктивной переменной наклона; значение параметра при фиктивной переменной. (20) стр.65
- •22..Алгоритм теста Дарбина-Уотсона на наличие (отсутствие) автокорреляции случайных возмущений. (20) стр 33
- •23. Структурная и приведённая формы спецификации эконометрических моделей.
- •24. Гетероскедастичность случайного возмущения. Причины. Последствия. Алгоритм теста Голдфельда-Квандта на наличие или отсутствие гетероскедастичности случайных возмущений.
- •Алгоритм теста Голдфелда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений.
- •25. Спецификация и оценивание мнк эконометрических моделей нелинейных по параметрам.
- •26. Способы корректировки гетероскедастичности. Метод взвешенных наименьших квадратов
- •27.Проблема мультиколлинеарности в моделях множественной регрессии.Признаки мультиколлениарности.
- •28.Что такое логит,тобит,пробит.
- •29. Что такое Метод наибольшего правдоподобия стр. 62.
- •30. Что такое стационарный процесс?
- •31.Свойства временных рядов.
- •32.Модели ar и var .
- •33. Идентифицируемость системы.
- •34. Настройка модели с системой одновременных уравнений.
- •35.Что такое метод Монте-Карло стр 53
- •36.Оценить качество модели по f, gq, dw (линейнные).Стр.33, 28-29
- •37. Оценка погрешностей параметров эконометрической модели методом Монте-Карло .
- •38. Отражение в модели влияния неучтённых факторов. Предпосылки теоремы Гаусса-Маркова.
- •39.Модели временных рядов. Свойства рядов цен акций на бирже (20) с.93.
- •40. Ожидаемое значение случайной переменной, её дисперсия и среднее квадратическое отклонение. (20) с.12-21
- •41. Оценка параметров парной регрессионной модели методом наименьших квадратов с использованием сервиса Поиск решения.
- •42. Проверка статистических гипотез, t-статистика Стьюдента, доверительная вероятность и доверительный интервал, критические значения статистики Стьюдента. Что такое “толстые хвосты”?
- •43.Проблема мультиколлинеарности в моделях множественной регрессии. Признаки мультиколлинеарности
- •44. Частные коэффициенты детерминации.
- •46. Экономический смысл коэффициентов линейного и степенного уравнений регрессии.
- •47.Оценка коэффициентов модели Самуэльсона-Хикса
- •48. Ошибки от включения в модель незначимых переменных или исключения значимых.С.80
- •49. Исследование множественной регрессионной модели с.74-79.
- •50. Мультиколлинеарность: чем плоха, как обнаружить и как бороться.
- •51. Признаки стационарности стохастического процесса. Что такое «Белый шум»? с.100
- •52. Структурная и приведённая формы спецификации эконометрических моделей.
- •53. Алгоритм проверки значимости регрессора в парной регрессионной модели. По t-статистике, по f-статистике.
- •54.Свойства рядов цен на фондовом рынке. Принципы построения портфеля Марковица с.93,102
- •55.Динамическая модель из одновременных линейных уравнений (привести пример) с.105.
- •56. Метод наибольшего правдоподобия: принципы и целесообразность использования
- •57. Этапы исследования модели множественной регрессии с.74-79.
34. Настройка модели с системой одновременных уравнений.
Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях - в правую часть системы:
y1 = b12* y2 + b13* y3 +… + b1n * yn + a11 * x1 + a12 * x2 +…+ a1m xm + e1,
y2 = b21* y1 + b23* y3 +… + b2n * yn + a21 * x1 + a22 * x2 +…+ a2m xm + e2,
yn = bn1* y1 + bn2* y2 +… + bnn-1 * yn-1 + an1 * x1 + an2 * x2 +…+ anm xm + en,
Система взаимозависимых уравнений получила название система совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. Экономические модели, значения переменных которых привязаны к моменту времени, называются динамическими.
Примером системы одновременных уравнений может служить модель спроса и предложения, включающая три уравнения.
В эконометрике эта система уравнений называется также структурной формой модели. В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассм. самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются специальные приемы оценивания .
Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные.
Эндогенные переменные - это зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через y.
Экзогенные переменные - это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них.
Обозначаются через x.
Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Эк. переменные могут выступать в одних моделях как эндогенные, а в других как экзогенные переменные. Внеэк. переменные (напр., климатич. условия, соц. положение, пол, возрастная категория) входят в систему только как экзогенные переменные. В качестве экзогенных переменных могут рассм. значения эндогенных переменных за предшествующий период времени (лаговые переменные).
Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.
Примером системы одновременных уравнений может служить модель спроса и предложения, включающая три уравнения.
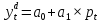
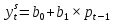
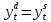
a1<0, b1>0
Второй пример:
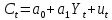
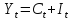
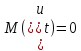
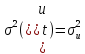
35.Что такое метод Монте-Карло стр 53
При работе на компьютере проще многократно проделать простые вычисления, чем один раз решить сложную аналитическую задачу. Поэтому для исследования стохастических моделей удобен метод Монте-Карло, позволяющий, в частности, оценивать погрешности параметров сложных моделей. Основные этапы реализации метода Монте-Карло:
1. Построение модели с “идеальными” параметрами.
2. Изменение значений переменных случайным образом в соответствии с дисперсией и законом распределения.
3. Расчет по проверяемой методике и сохранение параметров модели.
4. Возврат к п.2.
Пункты 2 и 3 выполняются заданное число раз – десятки, сотни, тысячи. В результате накапливаются массивы параметров, которые можно статистически обработать и установить надежность их оценок. В принципе, это можно сделать по аналитическим формулам дисперсионного анализа, но для сложной системы с внутренними связями такие расчеты становятся сложными и неустойчивыми.
