Вопросы и упражнения для самостоятельной работы

Установить, является ли следующее отображение инъективным, сюръективным, биективным:

а) — отображение из множества целых чисел в множество целых чисел, делящихся на 3, заданное формулой:;

б) — отображение из множества действительных чисел в полуинтервал, ставящее в соответствие каждому числуего дробную часть:;

в) — отображение из множества рациональных положительных чисел, ставящее в соответствие каждому рациональному числу, представленному в виде несократимой дроби, его числитель и знаменатель;

г) — отображение из множества действительных чисел, отличных от нуля, ставящее в соответствие 1 каждому положительному числуи –1 – отрицательному;

д) — отображение, которое ставит в соответствие числуостаток от деления числана 7;

е) — отображение, которое ставит в соответствие числуостаток от деления числана 6.

Пусть заданы следующие соответствия ииз множествав множество:

:,,,;

: ,,,.

Охарактеризовать соответствия и найти ,,.

§1.3. Бинарные отношения и их свойства

Бинарное отношение на множестве— это соответствие изв. Бинарное отношение однозначно определяется своим графиком. В дальнейшем мы не делаем различия между отношением и его графиком. Если, то будем писать, или, и говорить, чтоисвязаны отношением.

Отношение называетсярефлексивным, если оно содержит все пары вида, то естьдля любогоиз. Отношениеназываетсяантирефлексивным, если оно не содержит ни одной пары вида. Отношениеназываетсясимметричным, если вместе с каждой паройоно содержит также и пару. Отношениеназываетсяасимметричным, если невозможно одновременное выполнение условийи. Отношениеназываетсяантисимметричным, если одновременное выполнение условийиневозможно при, то естьвозможно только при. Отношениеназываетсятранзитивным, если вместе с любыми парамиионо содержит также и пару.

Рефлексивное, симметричное и транзитивное отношение называется отношением эквивалентности.Для обозначения отношений эквивалентности используется символ ~.

Пусть на множестве задано отношение эквивалентности. Для произвольного элементаобозначим черезмножество всех элементов, эквивалентных, т.е.. Множества виданазываютсяклассами эквивалентности. Классы эквивалентности непусты, не пересекаются между собой и их объединение дает все множество.

Отношением нестрогого порядка называют бинарное отношение на множестве, если оно рефлексивно, антисимметрично, транзитивно. Отношение называетсяотношением строгого порядка, если оно антирефлексивно, антисимметрично, транзитивно.

Примеры

1. Установить свойства указанных ниже отношений. Указать, какие из них являются отношениями эквивалентности или порядка. Для отношений эквивалентности построить разбиение на классы эквивалентности.

1. На множестве натуральных чисел :

а) ;

б) 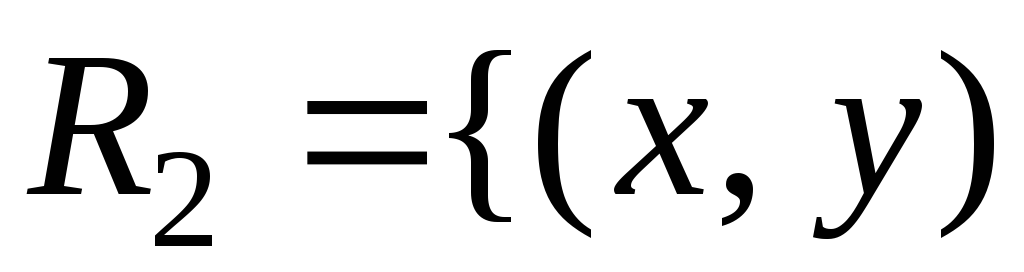|делит};

в) 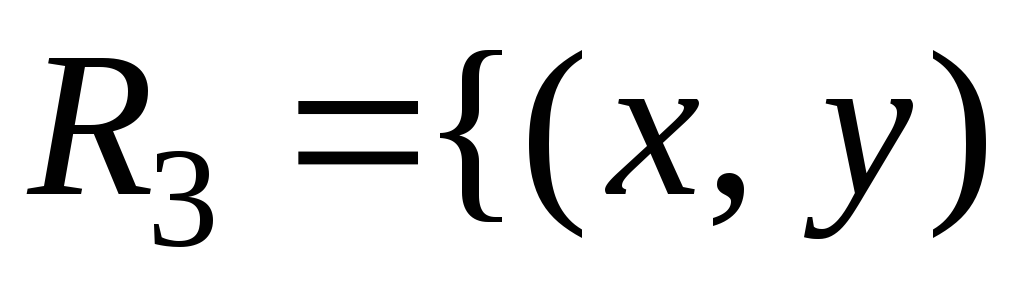|иимеют одинаковый остаток от деления на 4}.

2. На множестве точек действительной плоскости :

а) 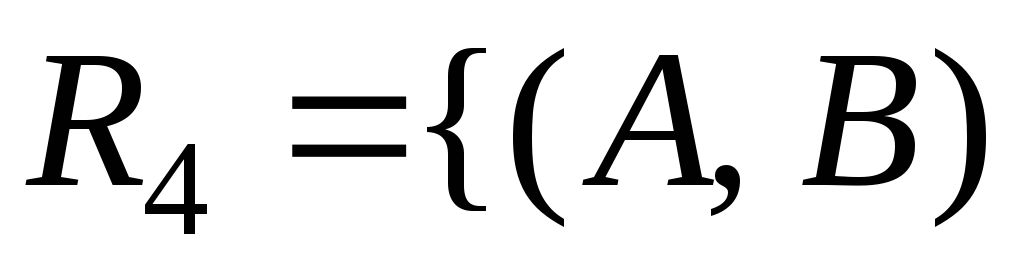|инаходятся на одинаковом расстоянии от начала координат};

б) 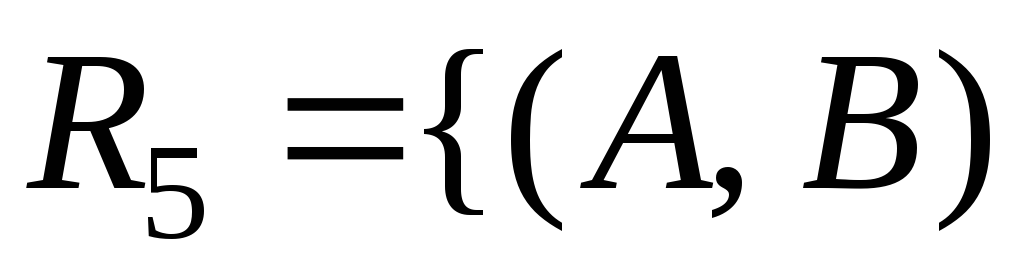|инаходятся на разном расстоянии от начала координат};

в) 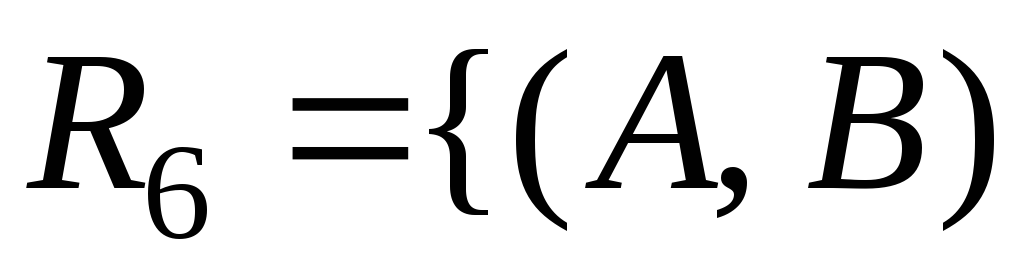|исимметричны относительно оси}.

3. На множестве всех подмножеств универсального множества :

а) 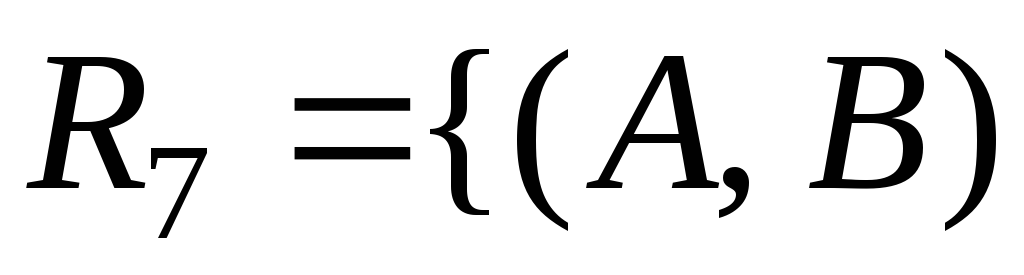|иимеют непустое пересечение};

б) 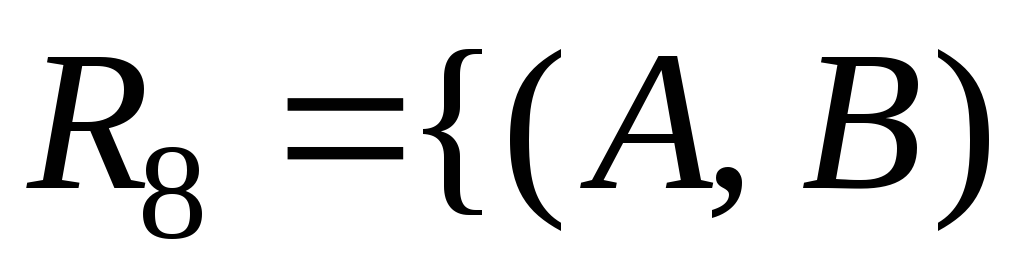|является подмножеством}.

4. На множестве людей:

а) 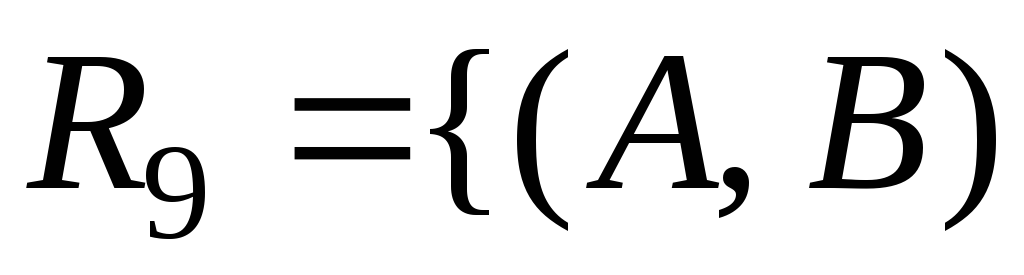|является сыном};

б) 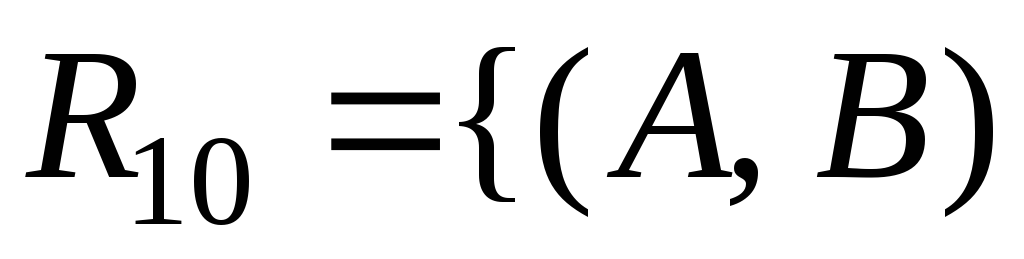|иживут в одном городе};

в) 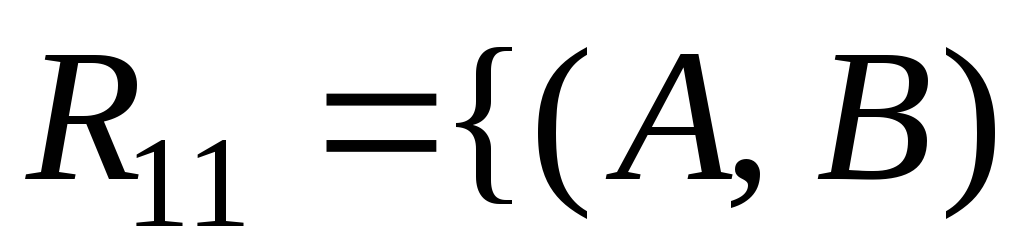|ибратья}.

Решение.1.На множестве натуральных чисел :

а) рефлексивно (т.к.для всех), не симметрично (т.к., но неверно, что), антисимметрично (т.к.), транзитивно (т.к.). Это отношение является отношением нестрогого порядка.

б) рефлексивно (т.к. любое число делит себя), не симметрично, антисимметрично (т.к. еслииделят друг друга, то они равны), транзитивно (т.к. если— делитель, а— делитель, то— делитель).

в) рефлексивно, симметрично, транзитивно и, следовательно, является отношением эквивалентности. Это отношение разбивает множествона 4 класса эквивалентности:,,,.

2. На множестве точек действительной плоскости :

а) рефлексивно, симметрично и транзитивно, следовательно, является отношением эквивалентности. Классы эквивалентности — это окружности с центром в начале координат.

б) Отношение антирефлексивно, симметрично, не транзитивно (возможен случай, когда точкиинаходятся на разном расстоянии от начала координат, точкиитакже на разном, а точкиина одинаковом расстоянии от начала координат).

в) не рефлексивно (если вторая координата точки отлична от нуля, то точка не симметрична себе), не антирефлекивно (точки осивсе же симметричны себе), симметрично, не транзитивно (например,и, но неверно).

3. На множестве всех подмножеств универсального множества :

а) : не рефлексивно (поскольку), не антирефлексивно (если, то всегда), симметрично, не транзитивно (возможно, чтоипересекаются,итакже пересекаются, ноине пересекаются).

б) : рефлексивно, не симметрично, антисимметрично, транзитивно. Следовательно,—отношение порядка.

4. На множестве людей:

а) антирефлексивно, асимметрично, не транзитивно;

б) рефлексивно, симметрично, транзитивно, следовательно, является отношением эквивалентности (классы — жители одного города);

в) антирефлексивно, не симметрично (возможны пары «сестра-брат»), не асимметрично (пары «брат-брат» симметричны), не транзитивно (— брат,— брат, ноне является братом самому себе).

2.Пусть. Построить отношение на множестве, которое:

а) рефлексивно, но не симметрично и не транзитивно;

б) симметрично, но не рефлексивно и не транзитивно;

в) транзитивно, но не рефлексивно и не симметрично.

Решение.а) Посколькурефлексивно, включаем впары. Полученное отношениесимметрично и транзитивно. Добавим к этому множеству пару. Тогда отношение уже не будет симметричным, но останется транзитивным. Если же добавить еще и пару, то отношение перестанет быть и транзитивным. Итак, указанными свойствами обладает, например, отношение.

б) Пусть сначала . Посколькудолжно быть симметричным, добавим кпару. Отношениесимметрично, не рефлексивно (не содержит, например,), не транзитивно (не следует). Следовательно, это искомое отношение. Если мы дополнительно потребуем, чтобы все элементы множестваприсутствовали в, то в качестве искомого отношения можно взять отношение.

в) Пусть сначала . Это отношение транзитивно, не симметрично и не рефлексивно, т.е. является искомым. Если мы дополнительно потребуем, чтобы все элементы множестваприсутствовали в, то в качестве искомого отношения можно взять.