
- •Оглавление
- •Примеры
- •Вопросы и упражнения для самостоятельной работы
- •§1.2. Отображения и соответствия
- •Операции над соответствиями
- •Примеры
- •Вопросы и упражнения для самостоятельной работы
- •§1.3. Бинарные отношения и их свойства
- •Примеры
- •Вопросы и упражнения для самостоятельной работы
- •§1.4. Логика высказываний
- •Логические операции над высказываниями
- •Примеры
- •Вопросы и упражнения для самостоятельной работы
- •§1.5. Логика предикатов
- •Примеры
- •Вопросы и упражнения для самостоятельной работы
Оглавление
Глава 1. Множества и математическая логика………………...5
§1.1. Множества и операции над ними………………………5
Вопросы и упражнения для самостоятельной работы………9
§1.2. Отображения и соответствия………………………….10
Вопросы и упражнения для самостоятельной работы…….13
§1.3. Бинарные отношения и их свойства………………….14
Вопросы и упражнения для самостоятельной работы…….20
§1.4. Логика высказываний………………………………….21
Вопросы и упражнения для самостоятельной работы…….25
§1.5. Логика предикатов……………………………………..26
Вопросы и упражнения для самостоятельной работы…….30
Глава 2. Метод математической индукции…………………..33
Вопросы и упражнения для самостоятельной работы…….38
Глава 3. Элементы комбинаторики…………………………...41
§3.1. Выборки………………………………………………...41
Вопросы и упражнения для самостоятельной работы…….49
§3.2. Биномиальные коэффициенты………………………..51
Вопросы и упражнения для самостоятельной работы…….57
Глава 4. Рекуррентные последовательности и производящие функции…………………………………………………………….60
§4.1. Линейные рекуррентные соотношения………………60
Вопросы и упражнения для самостоятельной работы…….67
§4.2. Производящие функции……………………………….69
Вопросы и упражнения для самостоятельной работы……..81
§4.3. Числа Фибоначчи………………………………………83
Вопросы и упражнения для самостоятельной работы…….86
Ответы…………………………………………………………..88
Литература………………………………………………………92
1. Множества и математическая логика
§1.1. Множества и операции над ними
Множество —
это совокупность каких-либо объектов,
называемых егоэлементами, обладающих
некоторым общим для ниххарактеристическим
свойством. Множество![]() являетсяподмножеством множества
являетсяподмножеством множества![]() (пишут:
(пишут:![]() ),
если всякий элемент множества
),
если всякий элемент множества![]() является элементом множества
является элементом множества![]() .
Множество, не содержащее ни одного
элемента, называют пустым и обозначают
символом. Удобно
считать, что все рассматриваемые
множества являются подмножествами
некоторогоуниверсальногомножества
.
Множество, не содержащее ни одного
элемента, называют пустым и обозначают
символом. Удобно
считать, что все рассматриваемые
множества являются подмножествами
некоторогоуниверсальногомножества![]() .
.
Операции над множествами
1. Пересечение
множеств![]() и
и![]() (пишут:
(пишут:![]() )
— это множество, состоящее из всех тех
элементов, которые принадлежат обоим
множествам
)
— это множество, состоящее из всех тех
элементов, которые принадлежат обоим
множествам![]() и
и![]() .
Если
.
Если![]() ,
то говорят, что множества
,
то говорят, что множества![]() и
и![]() не пересекаются.
не пересекаются.
2. Объединение
множеств![]() и
и![]() (пишут:
(пишут:![]() )
— это множество, состоящее из всех тех
элементов, которые принадлежат хотя бы
одному из множеств
)
— это множество, состоящее из всех тех
элементов, которые принадлежат хотя бы
одному из множеств![]() и
и![]() .
.
3. Разность
множеств![]() и
и![]() (пишут:
(пишут:![]() )
— это множество, состоящее из всех тех
элементов, которые принадлежат множеству
)
— это множество, состоящее из всех тех
элементов, которые принадлежат множеству![]() ,
но не принадлежат множеству
,
но не принадлежат множеству![]() .
.
4. Симметрическая
разность множеств![]() и
и![]() (пишут:
(пишут:![]() )
— это множество, состоящее из всех тех
элементов, которые принадлежат одному
из множеств
)
— это множество, состоящее из всех тех
элементов, которые принадлежат одному
из множеств![]() и
и![]() ,
но не принадлежат другому.
,
но не принадлежат другому.
5. Дополнение
множества![]() состоит из всех тех элементов множества
состоит из всех тех элементов множества![]() ,
которые не принадлежат множеству
,
которые не принадлежат множеству![]() .
Если
.
Если![]() — универсальное множество, определенное
контекстом, вместо
— универсальное множество, определенное
контекстом, вместо![]() пишут
пишут![]() .
.
6. Прямое (декартово)
произведение множеств![]() и
и![]() (пишут:
(пишут:![]() )
— это множество всех упорядоченных пар
)
— это множество всех упорядоченных пар![]() ,
где
,
где![]() и
и![]() .
.
Примеры
1. Пусть
универсальное множество![]() — множество всех сотрудников некоторой
фирмы;
— множество всех сотрудников некоторой
фирмы;![]() — множество всех сотрудников данной
организации старше 35 лет;
— множество всех сотрудников данной
организации старше 35 лет;![]() — множество сотрудников, имеющих стаж
работы более 10 лет;
— множество сотрудников, имеющих стаж
работы более 10 лет;![]() — множество менеджеров фирмы. Каковы
характеристические свойства элементов
следующих множеств:
— множество менеджеров фирмы. Каковы
характеристические свойства элементов
следующих множеств:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
д)
;
д)![]() .
.
Решение.а)![]() — множество сотрудников организации,
стаж работы которых не превышает 10 лет.
— множество сотрудников организации,
стаж работы которых не превышает 10 лет.
б)
![]() — множество менеджеров фирмы не старше
35 лет, имеющих стаж работы более 10 лет.
— множество менеджеров фирмы не старше
35 лет, имеющих стаж работы более 10 лет.
в)
![]() — множество всех сотрудников фирмы
старше 35 лет, а также сотрудников, не
являющихся менеджерами, стаж работы
которых более 10 лет.
— множество всех сотрудников фирмы
старше 35 лет, а также сотрудников, не
являющихся менеджерами, стаж работы
которых более 10 лет.
г)
![]() — множество сотрудников организации
со стажем работы более 10 лет, не работающих
менеджерами.
— множество сотрудников организации
со стажем работы более 10 лет, не работающих
менеджерами.
д)
![]() — множество менеджеров со стажем работы
не более 10 лет.
— множество менеджеров со стажем работы
не более 10 лет.
2. Пусть![]() ,
,![]() ,
,![]() ,
,![]() .
Найти: а)
.
Найти: а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г) ;
д)
;
д)![]() .
.
Решение.а)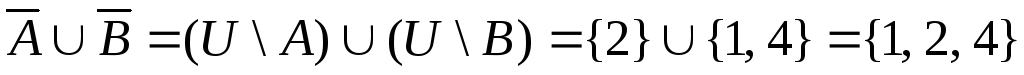 .
.
б)
 .
.
в)
 .
.
г)
 .
.
д)
![]() .
.
3. Доказать справедливость соотношения
![]() .
.
Решение.Множества![]() и
и![]() равны, если
равны, если![]() и
и![]() .
.
1. Покажем сначала,
что
![]() ,
т.е. любой элемент
,
т.е. любой элемент![]() из множества, заданного левой частью
соотношения, принадлежит и множеству,
заданному правой частью соотношения.
из множества, заданного левой частью
соотношения, принадлежит и множеству,
заданному правой частью соотношения.
Пусть
![]() .
Тогда
.
Тогда![]() принадлежит одновременно
принадлежит одновременно![]() и
и![]() ,
т.е.
,
т.е.![]() принадлежит одному из множеств
принадлежит одному из множеств![]() или
или![]() и множеству
и множеству![]() .
Следовательно,
.
Следовательно,![]() принадлежит либо
принадлежит либо![]() и
и![]() ,
либо
,
либо![]() и
и![]() .
Это означает, что
.
Это означает, что![]() принадлежит либо пересечению
принадлежит либо пересечению![]() ,
либо пересечению
,
либо пересечению![]() .
Значит,
.
Значит,![]() принадлежит объединению
принадлежит объединению![]() .
.
Это рассуждение можно записать с помощью формул:
Пусть
![]() .
Тогда
.
Тогда
![]() и
и
![]()
![]()
![]() (
(![]() или
или![]() )
и (
)
и (![]() )
)![]()
![]() (
(![]() и
и![]() )
или (
)
или (![]() и
и![]() )
)![]()
![]()
![]() или
или
![]()
![]()
![]()
![]() .
.
Таким образом,
![]() .
.
2. Покажем теперь,
что
![]() ,
т.е. любой элемент
,
т.е. любой элемент![]() из множества, заданного правой частью
соотношения, принадлежит и множеству,
заданному левой частью соотношения.
из множества, заданного правой частью
соотношения, принадлежит и множеству,
заданному левой частью соотношения.
Пусть
![]() .
Тогда
.
Тогда
![]() или
или
![]()
![]()
![]() (
(![]() и
и![]() )
или (
)
или (![]() и
и![]() )
)![]()
![]() (
(![]() или
или![]() )
и (
)
и (![]() )
)![]()
![]()
![]() и
и
![]()
![]()
![]()
![]() .
.
Следовательно,
![]() .
.
Таким образом,
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
4. Пусть![]() ,
,![]() .
Найти
.
Найти![]() ,
,![]() ,
,
![]() ,
,![]() .
.
Решение. Имеем:
![]() ;
;
![]() ;
;
![]() ;
;

