1. Множества и математическая логика
§1.1.
2. а)
,
б), в),
г)
,
д)
,
е)
.
3. а)
,
б)
,
в) {2}, г)
,
д)
,
е) {2}.
4.
,
,
.
5.
,
.
7.
,
.
§1.2.
8. а), в) инъективно, не сюръективно, б), г) не инъективно, сюръективно, д) биективно, е) не инъективно, не сюръективно.
9.
не функционально, сюръективно,
функционально, биективно.
§1.3.
10.
отношение эквивалентности; 2 класса:
множество четных чисел и множество
нечетных чисел;
антирефлексивное, симметричное, не
транзитивное;
отношение строгого порядка;
антирефлексивное, антисимметричное,
не транзитивное;
отношение эквивалентности; классы —
вертикальные прямые;
рефлексивно, симметрично, не транзитивно;
отношение эквивалентности; классы —
лучи, выходящие из начала координат;
антирефлексивно, симметрично, не
транзитивно;
,
отношение строгого порядка,
рефлексивно, симметрично, не транзитивно.
11.
— симметричные,
— рефлексивное и транзитивное,
— антисимметричное. 12.
,
;
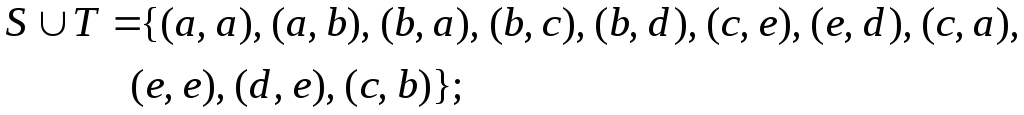
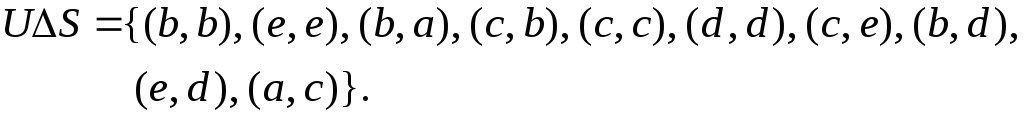
§1.4.
14. а), б), в) 1. 15. б) и г). 19. а), б) да; в) нет. 20. а) нет; б) и в) да.
§1.5.
21. а) 0; б) 1. 22. а), б), в) 0, 1; г) 0, 0. 23. 0; 1; 1; 1; 1; 1.
24. а) 0, 0, 0, 1; б) 1, 1, 0, 1; в) 0, 1, 1, 0, 0, 1. 25. а) 2-я и 3-я; б) 2-я.
26. а) 0, 1, 1, 1; б), г), д) 0, 1, 0, 0; в) 0, 1, 1, 0.
27. а) 0, 1, 1, 1; б) 0, 1, 1, 0. 28. а), в) 0, 1, 0, 0; б) 0, 1, 1, 0;
г) 0, 1, 1, 1. 29. а), б), ж) истинны; в), д), е) выполнимы; г) ложна.
2. Метод математической индукции
6.
.
7. а)
;
б)
;
в)
;
г)
.
3. Элементы комбинаторики
§3.1.
1. 322= 1024. 2. 2
= 992.
3.
– 8
– 8
= 40768.
4. 95. 5. 120. 6. 80. 7.
4! = 360.
8.
23! = 240.
9. 64! = 144. 10.
6! – 25! = 480.
11.
= 136.
12.
= 91.
13. 4
= 8845200.
14. 210–
–
–
= 968.
15.
= 84.
16.
= 120.
21. 32,47.
§3.2.
25. 792 – 560
.
26. 7803. 27.
.
28. 23670. 29.
.
31. 2n–1.
32. 3n. 33.
.
34. 35. 35.
.
36.
.
37. 1 – 5x + 15x2 – 35x3 +70x4 – 126x5.
38.
.
39. 1 + 10x + 51x2 + 180x3 + 498x4.
40.
.
41. 1. 42. 66.
4. Рекуррентные последовательности и производящие функции
§4.1.
1. 2n + 3n.
2.
.
3. (n + 2)3n.
4. (2n + 5)(–1)n. 5. 2(2 + i)n + 2(2 – i)n .
6. (1 – i)(1 + i
)n + (1 + i)(1 – i
)n .
7. sn+3 = 4sn+2 – 5sn+1 + 2sn ; sn = 2n+2 + n – 1.
8. sn+3 = –4sn+2 – 2sn+1 + 3sn ;
sn = 
.
9. 
.
10.un+3 = 3un+2 – 3un+1 + un .
§4.2.
11.
.
12.
=
=
.
13.
=
=
= 
.
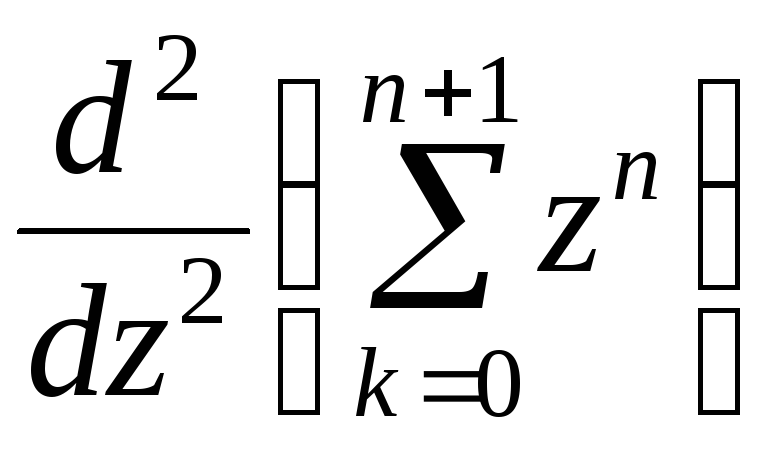14.
.
15. 
.
16. e2z – 1.
17.
.
18.
.
19. f(z) = 
;uk = –(k + 2) + 32k.
20. n2n–1.
21. 0. 22. n(n – 1)2n–1.
23.
.
24.
.
25. 670.
26. 50877. 27.
;
5n – 24n + 3n (приn 2).
28. 3n – 32n + 3 (приn 3).
§4.3.
37. 6765. 39.
.
40.
.
Указание: (Fk)3=
.
Литература
Гисин В.Б.Лекции по дискретной математике. Часть 1. — М.: Финансовая академия, 2001. — 196 c.
Гисин В.Б.Лекции по дискретной математике. Часть 2. — М.: Финансовая академия, 2003. — 156 c.
Андерсон Дж. Дискретная математика и комбинаторика. — М.: Издательский дом «Вильямс», 2003. — 960 с.
Москинова Г.И. Дискретная математика. Математика для менеджера в примерах и упражнениях: Учебное пособие. — М.: Логос, 2002. — 240 с.