Рис 4. Кривые асимметричных распределений

(пунктиром обозначена нормальная кривая).

Если вершина сдвинута влево, то правая часть кривой оказывается длиннее левой т.е. имеет место правосторонняя асимметрия, характеризующаяся неравенством

>Me>Mo,

что означает преимущественное появление в распределении более высоких значений признака.

Если же вершина кривой сдвинута вправо и левая часть оказывается длиннее правой, то асимметрия левосторонняя, для которой справедливо неравенство

<Me<Mo,

означающее, что в распределении чаще встречаются более низкие значения признака.

Чем больше величина расхождения между , Me, Mo, тем более асимметричен ряд.

В нормальном и близких к нему распределениях основная масса единиц (почти 70%) располагается в центральной зоне ряда, в диапазоне ().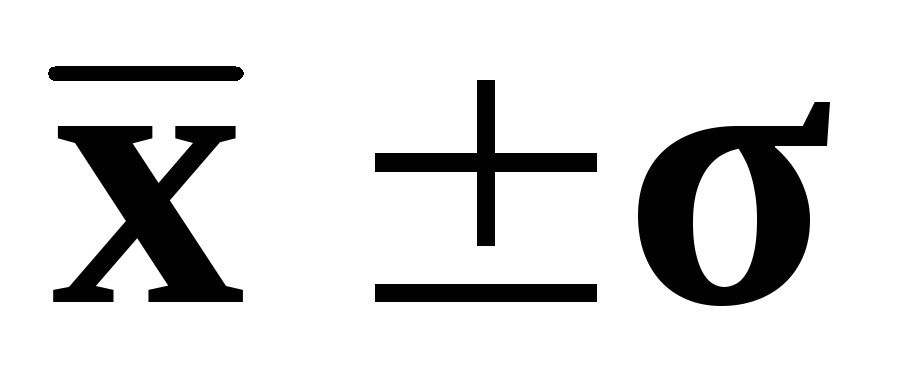

При правосторонней асимметрии As_п>0, при левосторонней As_п<0. Если As_п=0, вариационный ряд симметричен.

При As>0 имеет место правосторонняя асимметрия, при As<0 – левосторонняя. В симметричных распределениях As=0.

Чем больше величина |As|, тем более асимметрично распределение. Установлена следующая оценочная шкала асимметричности:

_|As|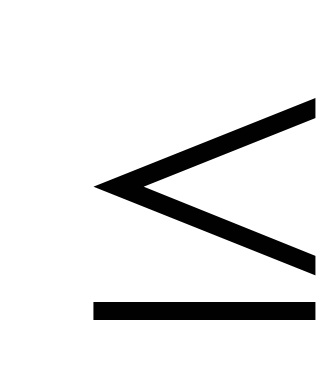0,25 - асимметрия незначительная;

0,25<|As|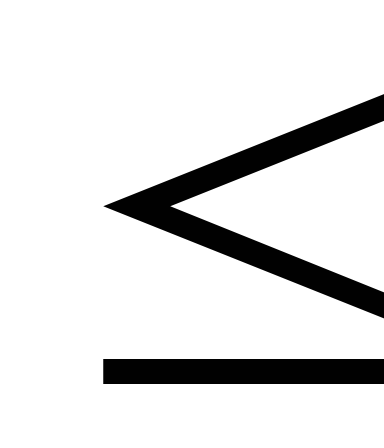0,5 - асимметрия заметная (умеренная);

|As|>0,5 - асимметрия существенная.

Показатель эксцессаEkхарактеризуеткрутизнукривой распределения - еезаостренностьилипологость по сравнению с нормальной кривой.

а) островершинное распределен б) плосковершинное распределение

Кривые распределения с ненулевым эксцессом

(пунктиром обозначена нормальная кривая).

Для нормального распределения Ek=0, поэтому чем больше абсолютная величина |Ek|, тем существеннее распределение отличается от нормального.

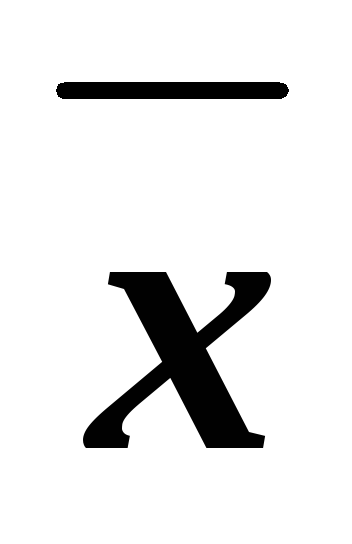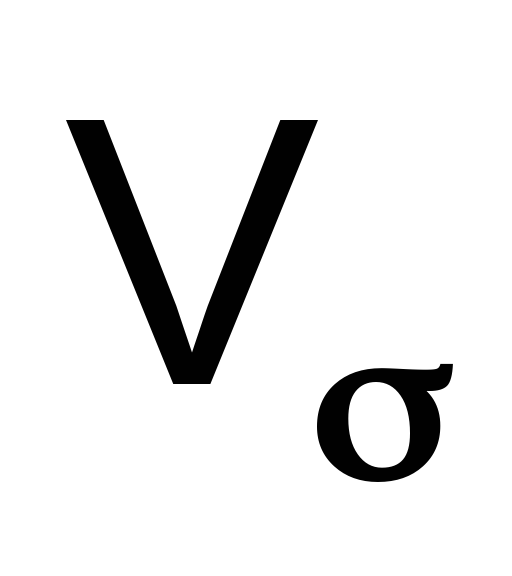Т.о. рассмотренные показатели , Mo, Me,, Аs, Ек позволяют определить форму кривой распределения.