Варианты контрольной работы1 №1 вариант 1 (для студентов, номера личных дел которых оканчиваются цифрой 1)

1. Даны матрицы:

и

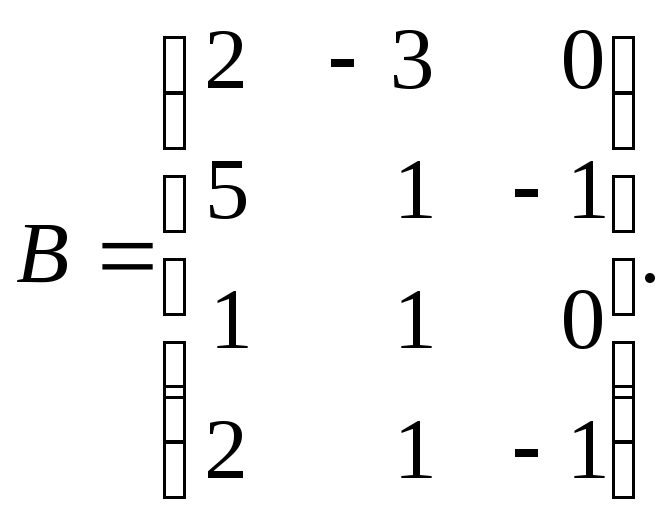
Найти матрицу и выяснить, являются ли строки матрицы С линейно зависимыми.

2. Методом обратной матрицы решить систему уравнений:

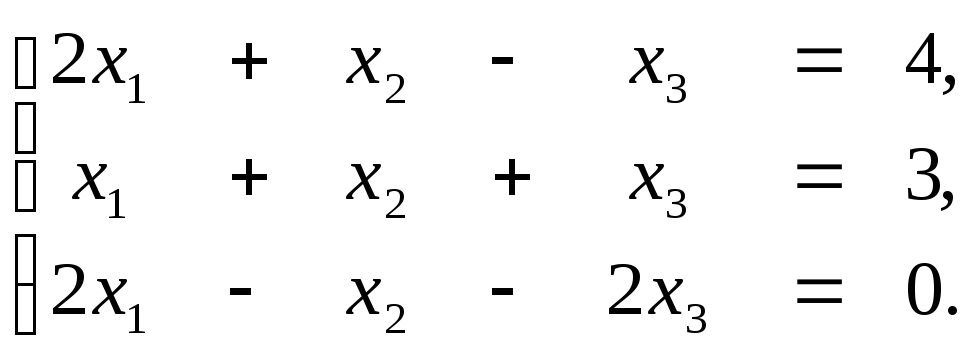
3. Методом Гаусса решить систему уравнений:

Найти одно из ее базисных решений.

4. Записать квадратичную форму в матричном виде. Привести ее к каноническому виду.

5. Точки ,иявляются вершинами треугольникаABC. Составить уравнение высоты треугольника, опущенной из точки А на сторону ВС. Определить координаты точки Н – основания высоты АН треугольника АВС. Сделать чертеж.

6. Найти значение параметра , при котором плоскостиибудут перпендикулярны.

Вариант 2 (для студентов, номера личных дел которых оканчиваются цифрой 2)

1. Даны матрицы:

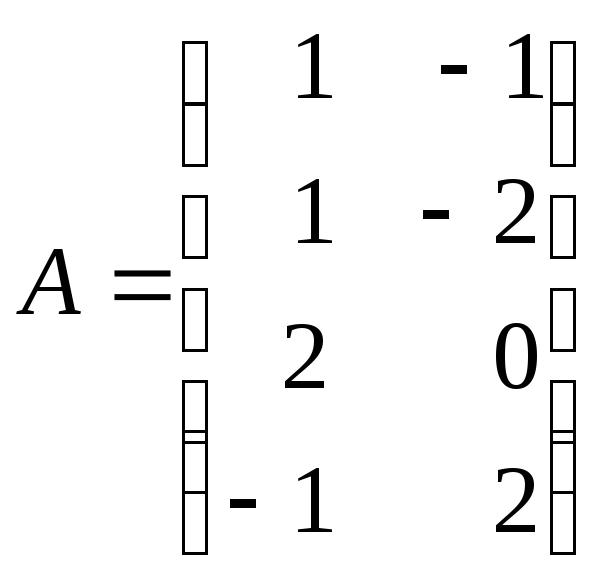и

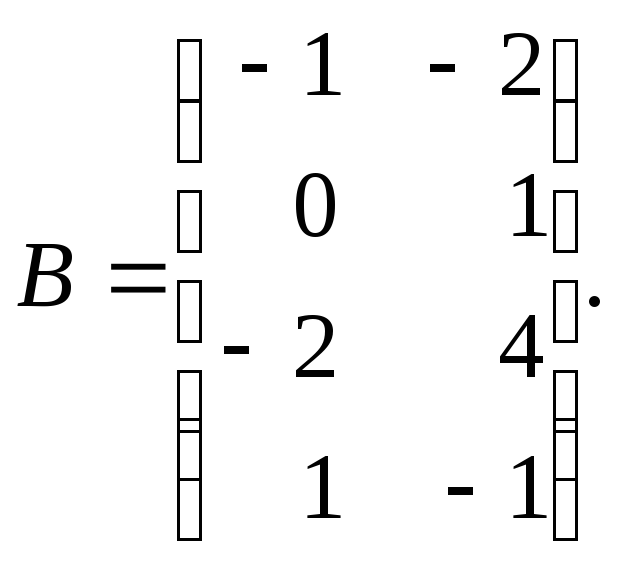
Найти матрицу и выяснить, имеет ли она обратную.

2. Методом Гаусса решить систему уравнений:

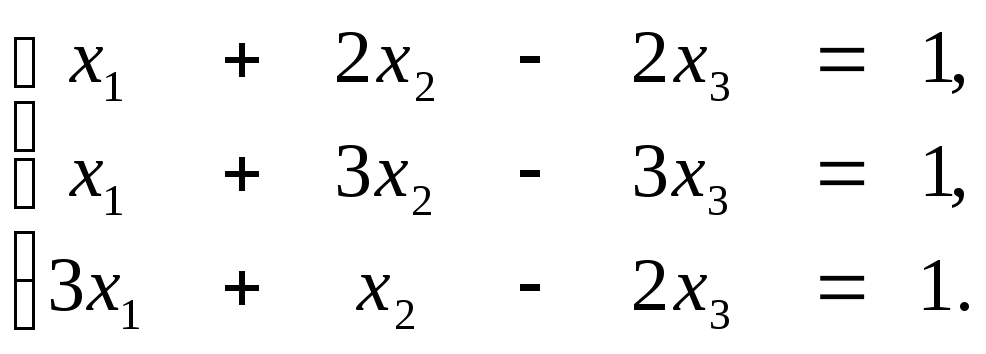
3. Выяснить, является ли совместной система уравнений:

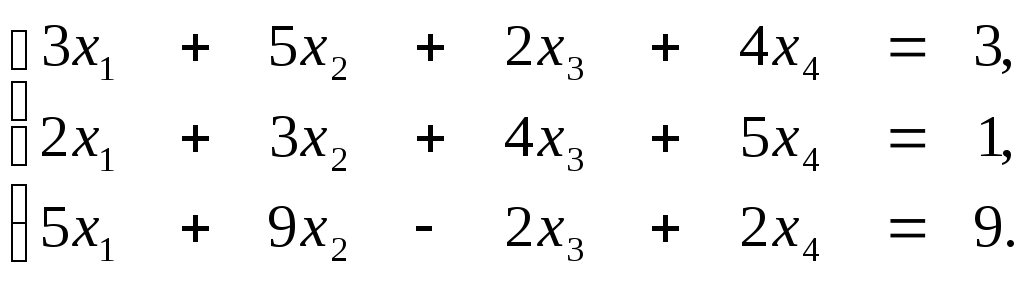
4. Найти собственные значения и собственные векторы линейного оператора , заданного матрицей.

5. Определить вид и расположение кривой второго порядка , приведя ее уравнение к каноническому виду. Составить уравнение прямой, проходящей через центр кривой второго порядка и точку. Сделать чертеж.

6. Найти значение параметра α, при котором прямые ибудут перпендикулярны.

Вариант 3 (для студентов, номера личных дел которых оканчиваются цифрой 3)

1. Решить матричное уравнение

,

где

2. По формулам Крамера решить систему уравнений:

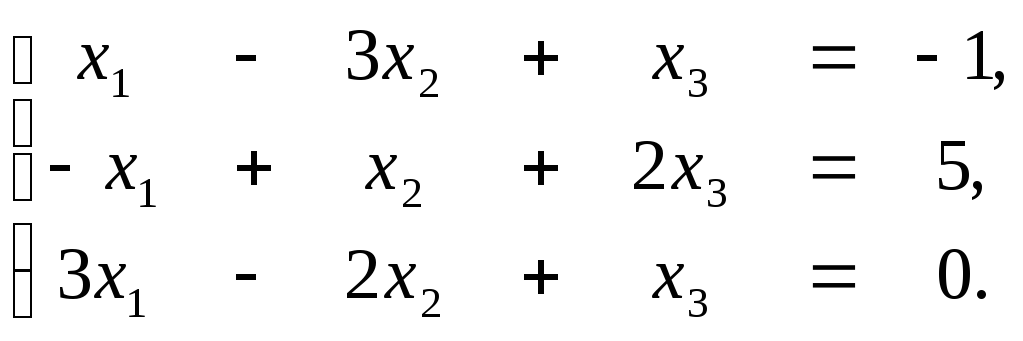
3. Методом Гаусса решить систему уравнений:

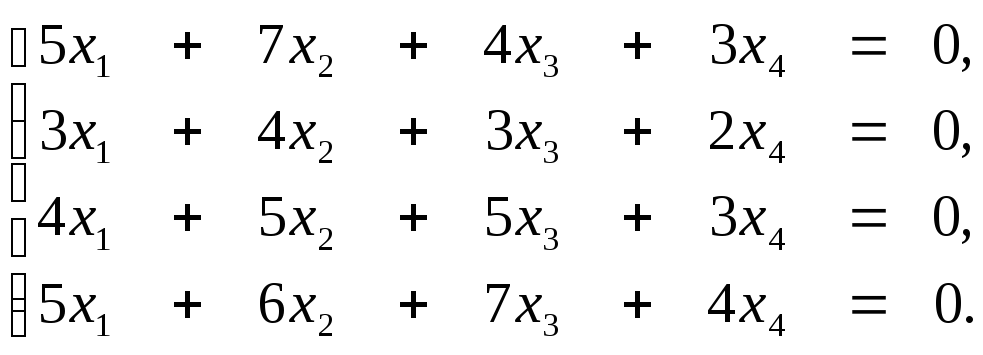
4. Найти угол между векторами и, если известно, что,,,и угол между векторамииравен.

5. Определить вид и расположение кривой второго порядка . Составить уравнение прямой, проходящей через ее центр перпендикулярно прямой. Сделать чертеж.

6. Найти угол между прямой и плоскостью.

Вариант 4 (для студентов, номера личных дел которых оканчиваются цифрой 4)

1. Даны матрицы:

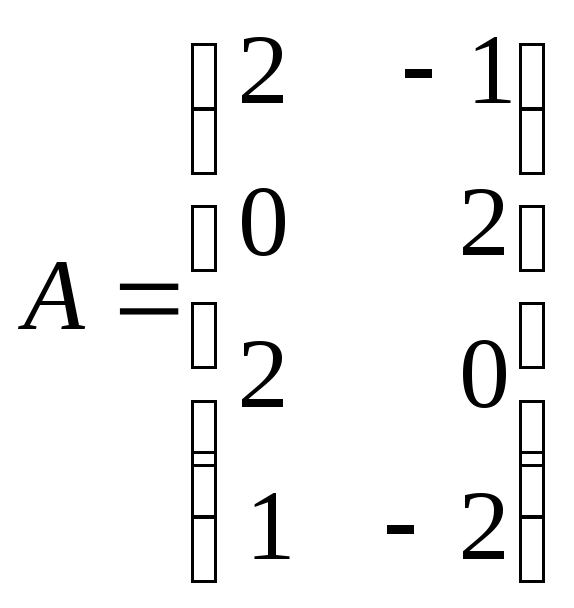и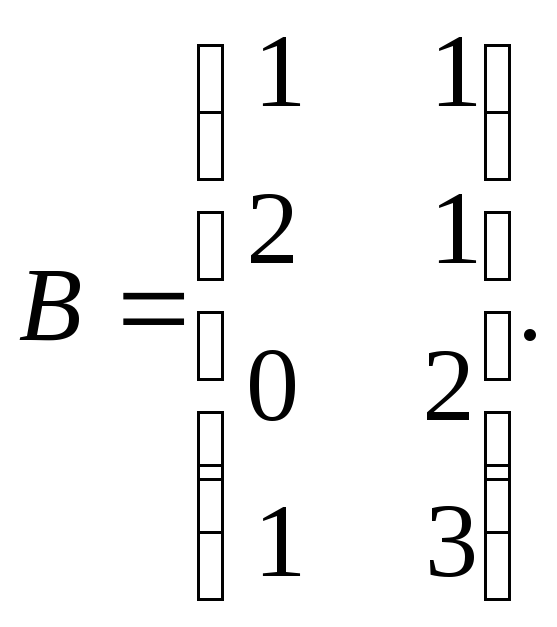

Найти матрицу и определить ее ранг.

2. Методом обратной матрицы решить систему уравнений:

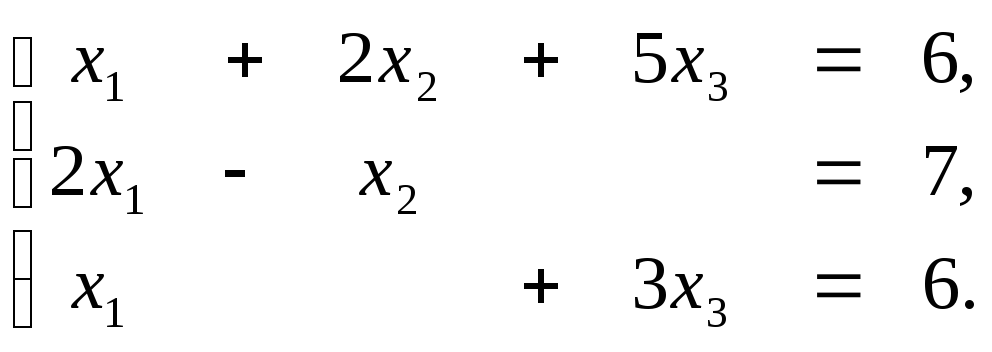
3. Методом Гаусса решить систему уравнений:

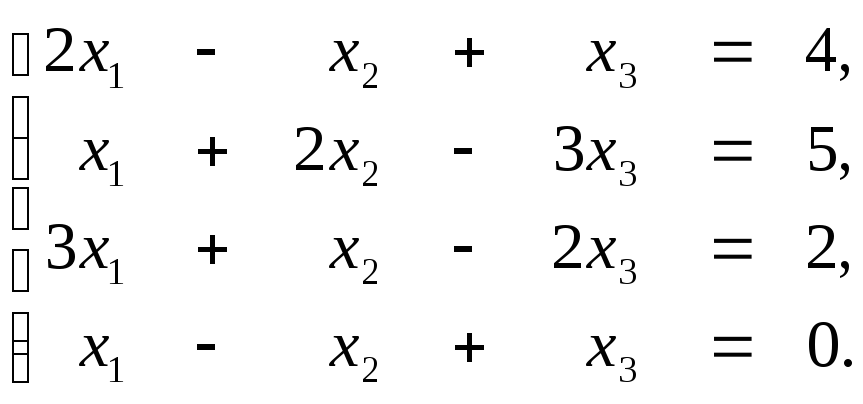
4. Проверить, что векторы ,иобразуют базис в пространстве.

5. Определить вид и расположение кривой второго порядка , приведя ее уравнение к каноническому виду. Найти уравнение прямой, проходящей через центр кривой второго порядка и точку. Сделать чертеж.

6. Составить уравнение плоскости, проходящей через точки ипараллельно оси.

Вариант 5 (для студентов, номера личных дел которых оканчиваются цифрой 5)

1. Решить матричное уравнение

,

где

,,

2. По формулам Крамера решить систему уравнений:

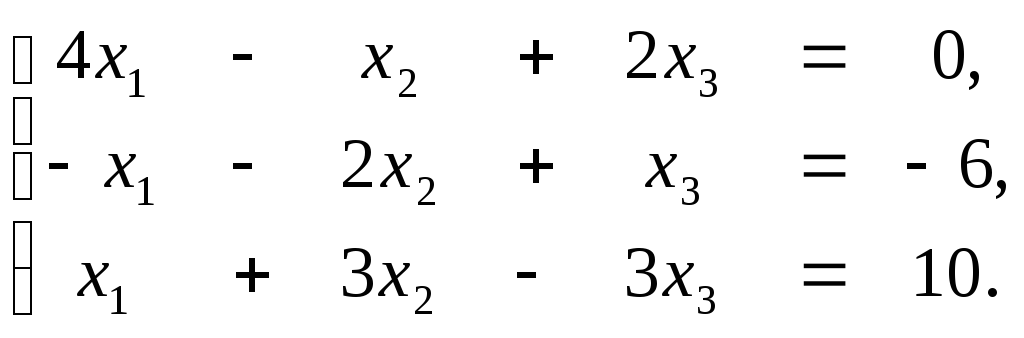
3. Методом Гаусса решить систему уравнений:

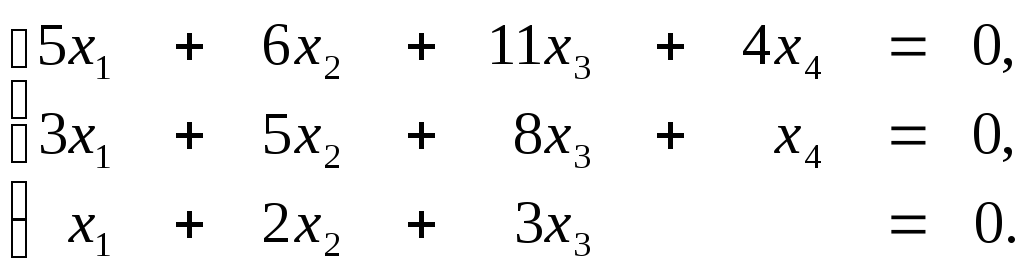
4.Найти вектор , коллинеарный вектору, такой что скалярное произведение, если известно, что вектор.

5. Определить вид и расположение кривой второго порядка , приведя ее уравнение к каноническому виду. Составить уравнение прямой, проходящей через вершину кривой второго порядка и точку. Сделать чертеж.

6. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору.