28. Неравенство Маркова (лемма Чебышева) (с выводом). Пример.

Пусть с.в.Х принимает только неотриц.знач.и имеет м.о.. Тогда для любого положит.А, верно неравенство:

А›0

След.

29. Неравенство Чебышева (с выводом) и его частные случаи для случайной величины, распределенной по биномиальному закону, и для частости события.

Т. Для любойс.в.,имеющей м.о.и дисперсию, справедливо нер.Чебышево:

где a=M(X),ε›0

Док. Обознач. a=M(X), рассмотрим Y=(X-a)²

Она прин.только не отриц. знач. M(Y)=M(X-a)²=D(X),т.е. у неё есть м.о.,след.к Y можно прим.нер-во Маркова

P(Y>)≤M(Y)/A

Возьмём A=ε², P(Y>ε²)≤D(X)/ε²

Y>ε²след. (X-a)²>ε²

Т.о. (А) примет вид

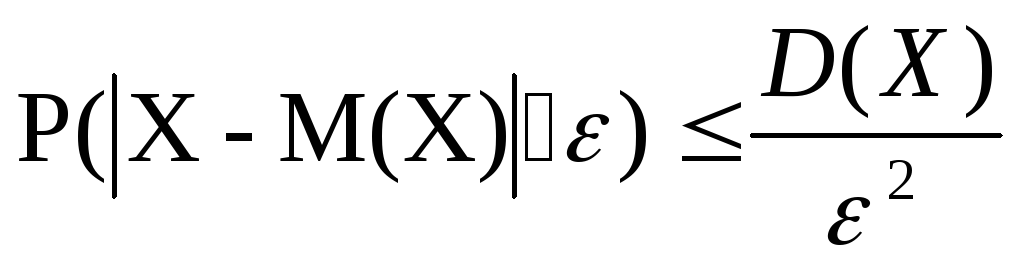
1.с.в.Х-бинум.зак.

2.Пусть W-частота соб.в n незав.повтор.исп.

W=X_n/n X_n-сколько раз произош.соб

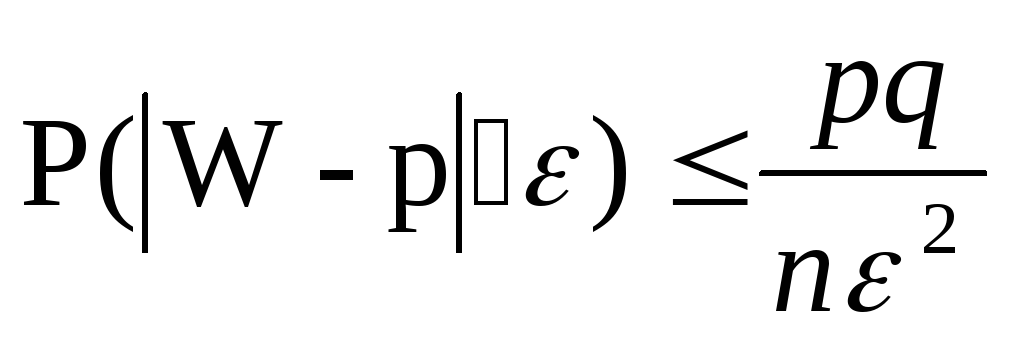
3.Пусть X1..Xn-незав.с.в., M(X)=a_i D(X)≤C

Тогда

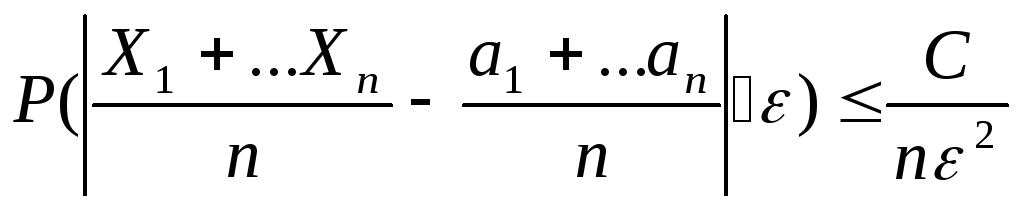
30. Неравенство Чебышева для средней арифметической случайных величин (с выводом).

Т.Бенулли Частость события в n независимых испытаниях, в каждом из которых оно может произойти с одной и тойже вер-ю p,при неограниченном увеличении числа n сходится к вер-ти p этого соб-я в отдельном исп-и

Или

Вытекает из нер-ва Чебышева для частости собятия:

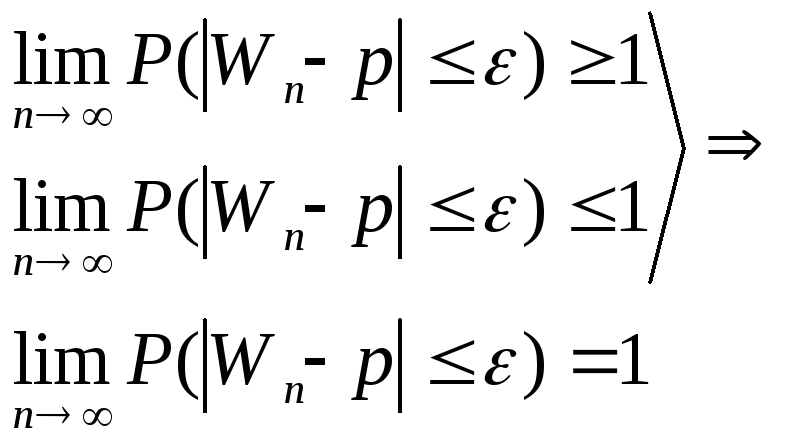
31. Теорема Чебышева (с доказательством), ее значение и следствие. Пример.

Пусть с.в.Х1..Хn имеют одинаковое м.о. а и дисперсия ограниченна одной и той же постоянной С,тогда верно:

M(Xi)=a D(Xi)≤C тогда

Вытекает из нер-ва Чебышева для частости собятия:

Смысл: При большом числе Х с.в. Х1…Хn практически достоверно, что их сред.ариф., которая явл.с.в.сколь мало отличается от конкретного числа a, т.е.практически перестаёт быть с.в..

Т.Чеб.принято наз.законом больших чисел. –это общ. принцип согласно кот.действия большого числа случ.факторов при весьма общих условиях приводит к результату почти независищяму от случая.

32. Закон больших чисел. Теорема Бернулли (с доказательством) и ее значение. Пример.

Т.Бенулли Частость события в n независимых испытаниях, в каждом из которых оно может произойти с одной и тойже вер-ю p,при неограниченном увеличении числа n сходится к вер-ти p этого соб-я в отдельном исп-и

Или

Вытекает из нер-ва Чебышева для частости собятия:

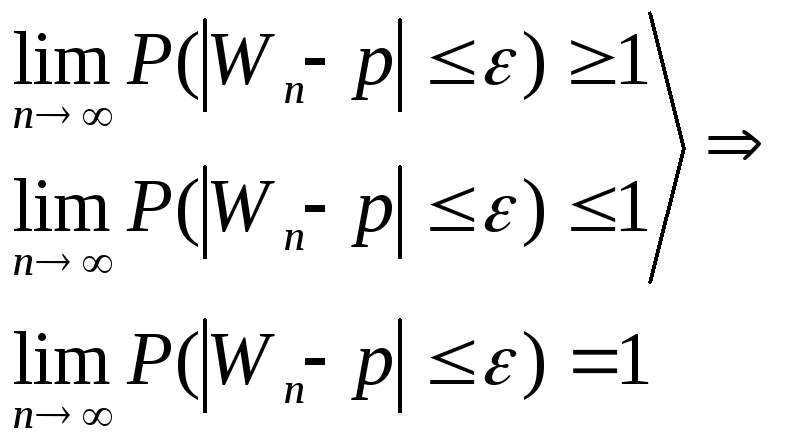
Смысл: При большом числе n практически достоверно, что частость собятия m/n величина случайная ,как угодно мало отличается от неслуч.вел. p-вер-ти соб-я,т.е.практически перестаёт быть слууч.

Т..принято наз.законом больших чисел. –это общ. принцип согласно кот.действия большого числа случ.факторов при весьма общих условиях приводит к результату почти независищяму от случая.

33. Вариационный ряд, его разновидности. Средняя арифметическая и дисперсия ряда. Упрощенный способ их расчета.

Пусть имеется некотор. признак Х,котор. подлежит изучению. Значение признака х назыв. их вариантами. Рассмотрим совокупность элементов – носителей признака. Кол-во элементов назыв. объемом совокупности. ; Если признак х принимает изоли-рованные значения, то он назыв. дискретным, если знач. Признака заполняют нек. интервал, то он интервальный. Пример: Х- размер обуви  дискретный признак; Х- ростинтервальный признак. Кол-во элементов совокупности, кот обладает данными значениями признака назыв. частотой этой варианты. Суммы всех частот = n. ni=n; (ni/n)=Wi.; Опр.: Вариационным рядом называется таблица, содержащая варианты в порядке возрастания и соответствующие им частоты или частости. Вариационный ряд – дискретный если варианты дискретны. Если признак принимает непрерывные значения, то интервал его значения разбив. на частности соответствующими частотами или частостями – такой ряд –интервальный.

Характеристики вариационного ряда.

1) Среднее значение 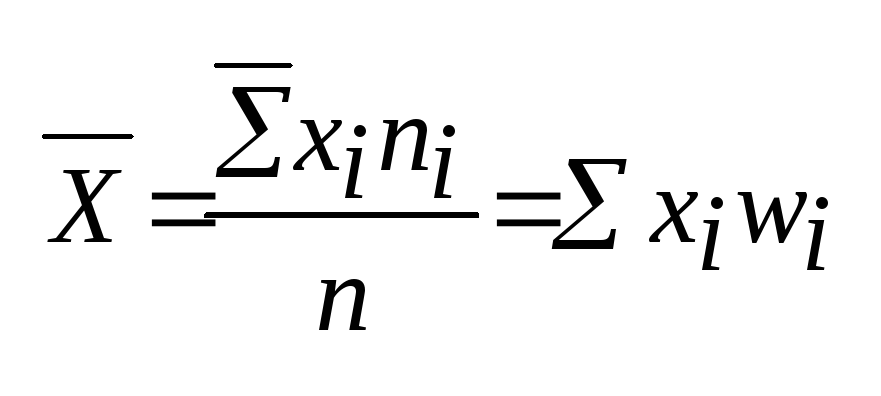Ср. знач. вар. ряда явл. аналогом мат. ожидатия

случайной величины.; 2)Диспер. вар. ряда явл аналогом дисперсии случ. величины.; 3)Среднеквадратич. Отклонения  =из квадрат.; Упрощённый метод вычисления хар-к вариацион. ряда. Пусть К- разность между сосед-ними значениями варианта. С- это наиболее часто встречающаяся варианта или варианта, стоящая в середине ряда.

34. Генеральная и выборочная совокупности. Принцип образования выборки. Собственно-случайная выборка с повторным и бесповторным отбором членов. Репрезентативная выборка. Основная задача выборочного метода.

Вся подлезащая изучению совокупность объектов (наблюдений) наз-ся генеральная совокупность. В матем.стат.понятие ген. совокуп.трактуется как совокуп.всех мыслимых наблюдений,которые могли бы быть произведены при данном комплексе условий. Понятие ген.сов.в определённом смысле аналдогично понятию с.в..Та часть объектов,которая отобрана отобрана для непосредственного изучения из ген.сов.,наз-ся выборочной совок. или выборкой.Сущность ывборочного метода состаит в том что бы по некоторой части ген.сов.(по выборке) выносить суждения о её св-вах в целом.Собственно-случювыб., оброзуется случ.выборром элементов без расчленения на части или группы.

Повторный-когда каждый элемент,случайно отобранный и обследованный, возвращается в общую совокуп.и может быть повторно отобран.

Бесповтор.-наоборот

Выб наз-ся репрез.если она достат.хор.воспроизвод.ген.совок.