
- •Краткий конспект лекций по теории вероятностей Лекция1 Вероятность
- •Действия над событиями.
- •Классификация событий Событие, состоящее из всех элементарных событий, не содержащихся в а, обозначим и будем называть противоположным событием.
- •Полная группа событий – это совокупность n событий а1, а2, …, Аn, одно из которых обязательно произойдет, т.Е. Свойства операций над событиями
- •Правило двойственности (теорема де Моргана)
- •Алгебра событий.
- •Вероятность. Классическое определение вероятности события
- •Геометрическая вероятность
- •Статистическая вероятность
- •Свойства вероятности
- •Лекция 2 Условная вероятность.
- •Формула вероятности произведения событий (теорема умножения вероятностей). Независимые события
- •Формула вероятности суммы совместных событий (теорема сложения вероятностей)
- •Формула полной вероятности
- •Формула Байеса (теорема гипотез)
- •Лекция 3. Случайные величины
- •Лекция 4 Повторные испытания.
- •Распределения, связанные с повторными испытаниями.
- •Лекция 5
- •Лекция 6. Двумерные случайные величины
- •Свойства функции распределения.
- •Свойства плотности.
- •Свойства коэффициента корреляции.
- •Двумерное равномерное распределение
- •Двумерное нормальное распределение
- •Задача линейного прогноза.
- •Лекция 7. Законы больших чисел и центральная предельная теорема. Неравенства Чебышева.
- •Законы больших чисел.
- •Теорема Чебышева
- •Обобщенная теорема Чебышева.
- •Теорема Маркова.
- •Теорема Бернулли.
- •Предельные теоремы.
- •Теорема Ляпунова.
- •Теорема Леви – Линдеберга.
- •Интегральная теорема Муавра – Лапласа.
- •Лекция 8 Элементы математической статистики
- •Основные задачи статистики.
- •Эмпирические законы распределения.
- •Точечные оценки параметров распределения.
- •Требования к оценкам.
- •2. Несмещенная, состоятельная оценка дисперсии
- •Интервальные оценки.
- •Доверительные интервалы для параметров нормального закона распределения. Доверительный интервал для математического ожидания.
- •Доверительный интервал для среднеквадратического отклонения .
Теорема Ляпунова.
Пусть Xk– независимые случайные величины,
имеющие математические ожиданияM(Xk)
=mkи
дисперсииD(Xk)
=Dk.
Обозначим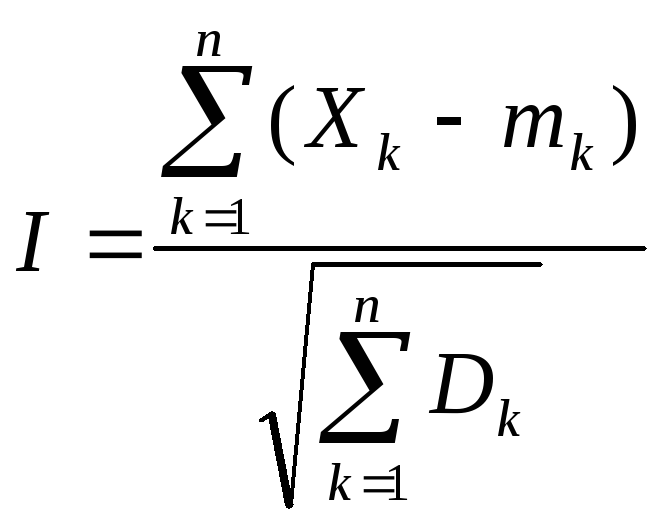 .
Если можно подобрать такое
.
Если можно подобрать такое![]() ,
что
,
что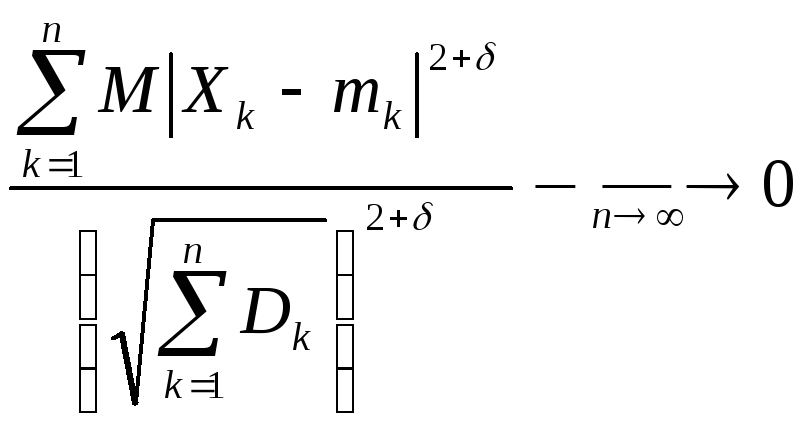 ,
то при
,
то при![]()
![]() равномерно поx.
равномерно поx.
Теорема Леви – Линдеберга.
Пусть Xk– независимыеодинаково распределенные
случайные величины, имеющие
математические ожиданияM(Xk)
=mи дисперсииD(Xk)
=
![]() .
Обозначим
.
Обозначим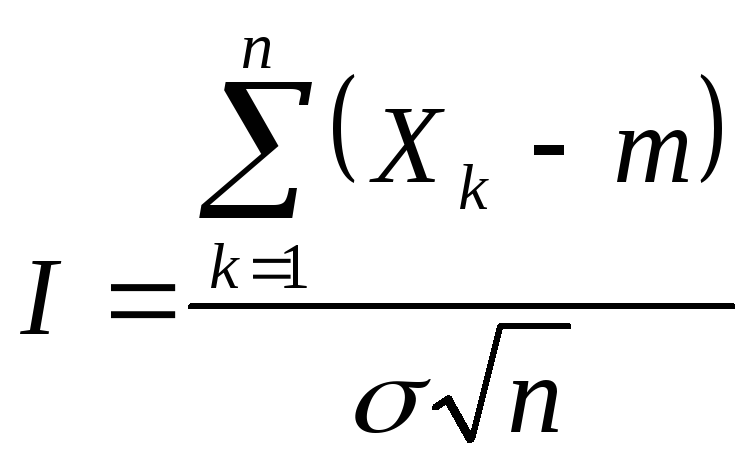 .
Тогда при
.
Тогда при![]()
![]() равномерно поx.
равномерно поx.
Замечание. В
теореме Леви – Линдеберга (ее чаще всего
и называют центральной предельной
теоремой)
![]() ,
условие
,
условие выполнено, оно превращается в
выполнено, оно превращается в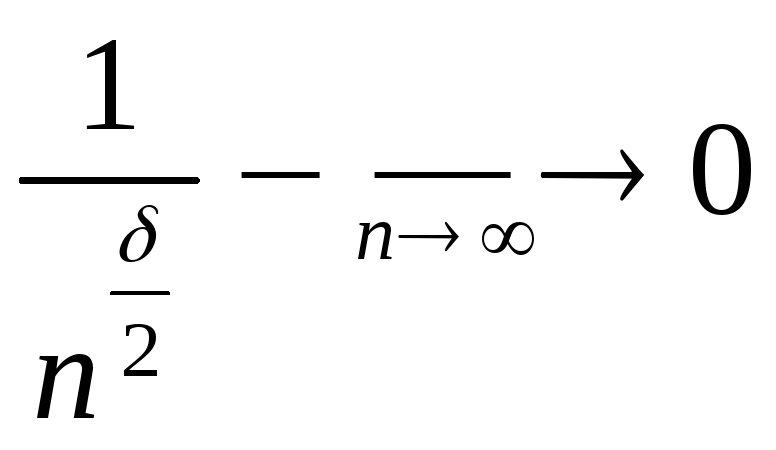 (проверьте сами) из-за требования
«одинаковости распределений», т.е.
равенства вкладов случайных величин в
случайную величину
(проверьте сами) из-за требования
«одинаковости распределений», т.е.
равенства вкладов случайных величин в
случайную величину![]()
![]() .
.
Если рассматривать схему Бернулли, то из теоремы Леви – Линдеберга следует интегральная теорема Муавра – Лапласа.
Интегральная теорема Муавра – Лапласа.
Пусть производится
nнезависимых испытаний,
в каждом из которых с вероятностьюpможет появиться событие А. Обозначим![]() -
число появлений события вk–ом испытании (
-
число появлений события вk–ом испытании (![]() ).
Обозначим
).
Обозначим
![]() - общее число появлений события вnиспытаниях (
- общее число появлений события вnиспытаниях (![]() ).
Обозначим
).
Обозначим![]() .
Тогда при
.
Тогда при![]()
![]() равномерно поx.
равномерно поx.
Отсюда следует практическое правило вычисления
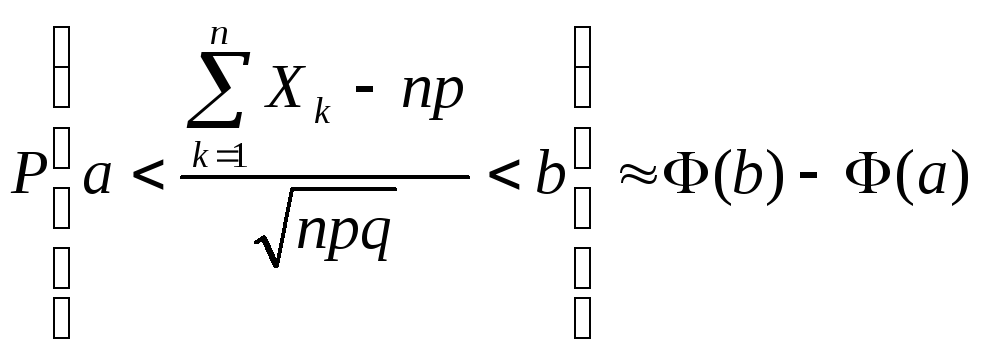
![]() ,
где
,
где
![]()
![]() .
Так как
.
Так как![]() то
заменим
то
заменим
![]() на
на![]() ,
,
![]() на
на![]() ,
,
![]() Получим
формулу для вероятности нахождения
числа успехов в заданном интервале:
Получим
формулу для вероятности нахождения
числа успехов в заданном интервале:
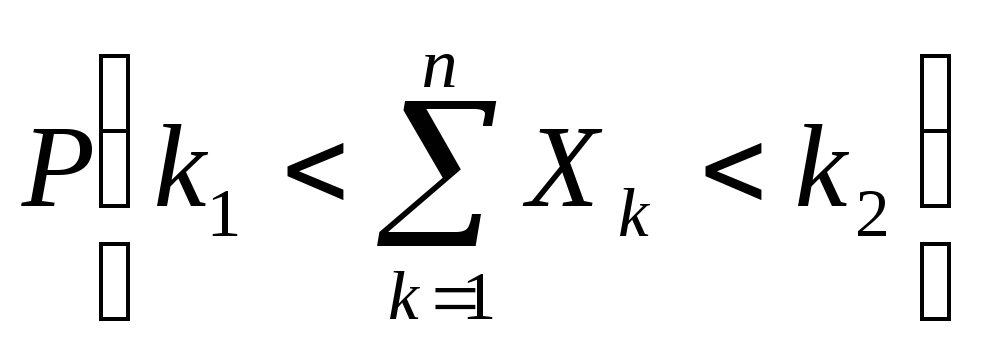 =
=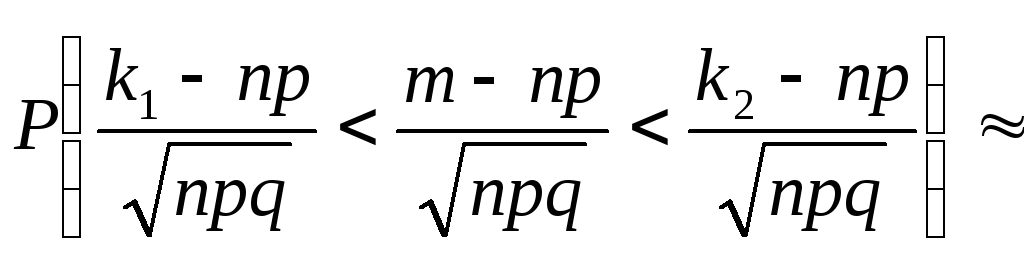
![]() -
-![]() .
.
Заменим
![]() на
на![]() ,
,
![]() на
на![]() .
.
Тогда
![]() .
.
Но
![]() .
.
Поэтому справедлива формула для вычисления отклонения частоты от вероятности
![]() ,
,
Если
интервал симметричный, т.е.
![]() ,
то по нечетности функции Лапласа получим
,
то по нечетности функции Лапласа получим
![]() .
.
Пример. Вероятность появления события p= 0,8. Сделаноn= 100 независимых испытаний. Найти вероятность того, что событие произойдет не менее 75 и не более 90 раз.
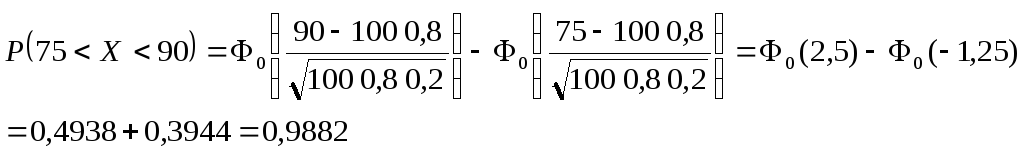
Пример. Бюффон бросил монету 4040 раз и получил герб 2048 раз. Найти вероятность отклонения частоты появления герба от вероятности.
![]()
![]()
Лекция 8 Элементы математической статистики
Пусть исследуется случайная величина с заранее неизвестной функцией распределения F(x).
Множество всех значений этой случайной величины называется генеральной совокупностью (Г С).
Единичное значение случайной величины называется выборкой объема 1.
Совокупность nзначений случайной величины образуютвыборку объема n.
Выборка имеет то же распределение, что и генеральная совокупность.
Выборочные значения называются вариантами.
Изучая выборку, делают заключение о вероятностных свойствах Г С.
Основные задачи статистики.
Оценка неизвестных параметров распределения:
точечные оценки параметров распределения, например оценка математического ожидания, дисперсии, моментов распределения,
интервальные оценки –доверительные интервалы – интервалы, в которых находятся параметры распределения сдоверительной вероятностью.
Проверка статистических гипотез– предположений о законе распределения ГС
или параметрах распределения.
Установление формы и степени связи между несколькими случайными переменными.
Эмпирические законы распределения.
Вариационным рядом называются варианты, расположенные в порядке их возрастания (не убывания, если варианты повторяются).
Будем обозначать
xk–
различные варианты вариационного ряда
(k= 1, 2, …),nk– их частоты (число повторений варианты),![]() - относительные частоты.
- относительные частоты.
Существуют различные формы закона распределения: ряд распределения, полигон частот, полигон относительных частот, эмпирическая функция распределения, гистограмма (дискретный аналог плотности распределения).
Рассмотрим, например, вариационный ряд 0,0,0,0.0.1,1,3,5,5. Объем выборки n= 10.
Ряд распределения
-
xk
0
1
3
5
nk
5
2
1
2
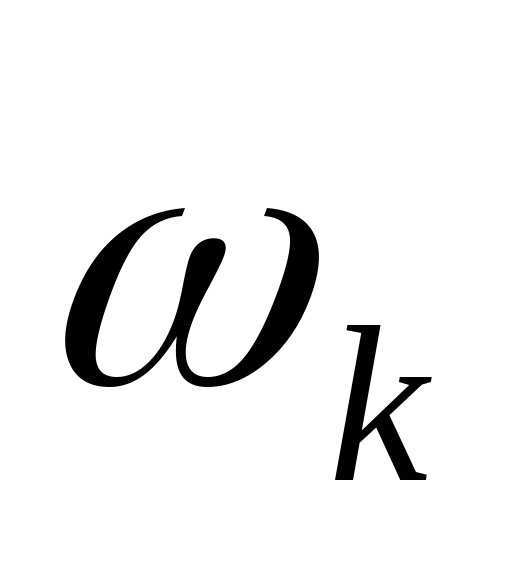
1/2
1/5
1/10
1/5
Полигон частот
П
 олигон
относительных частот имеет тот же вид,
но по оси ординат откладываются не
частотыnk,
а относительные частоты
олигон
относительных частот имеет тот же вид,
но по оси ординат откладываются не
частотыnk,
а относительные частоты![]() (на рисунке черточками отмечены единицы
по осям значений и частот).
(на рисунке черточками отмечены единицы
по осям значений и частот).
Xk
1 2 3 4 5
Эмпирическая функция распределения - аналог функции распределения для дискретных случайных величин, она тоже кусочно постоянна и имеет тот же график, только скачки функции в точках – вариантах происходят на относительные частоты вариант (в примере скачки от 0 на 0,5, затем на 0,2 до 0,7, затем на 0,1 до 0,8 и, наконец на 0,2 до единицы).
F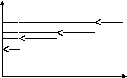 n(x) Эмпирическая
функция распределения формально
определяется как
n(x) Эмпирическая
функция распределения формально
определяется как
1
![]() , где
, где![]() - число
- число
0,4 членов выборки, меньших x.
1 2 3 4 5 x
Д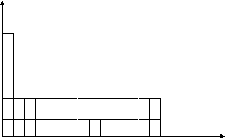 ля
построения гистограммы приходится
приписывать значение частоты варианты
некоторому интервалу стандартной ширины
(в нашем случае, например, 0,5), лежащему
справа от варианты так, чтобы площадь
ступени над интервалом равнялась
относительной частоте варианты.
ля
построения гистограммы приходится
приписывать значение частоты варианты
некоторому интервалу стандартной ширины
(в нашем случае, например, 0,5), лежащему
справа от варианты так, чтобы площадь
ступени над интервалом равнялась
относительной частоте варианты.






 1 0,4 0,2 0 0,5 1 1,5 3 3,5 5 5,5
1 0,4 0,2 0 0,5 1 1,5 3 3,5 5 5,5
