
- •Краткий конспект лекций по теории вероятностей Лекция1 Вероятность
- •Действия над событиями.
- •Классификация событий Событие, состоящее из всех элементарных событий, не содержащихся в а, обозначим и будем называть противоположным событием.
- •Полная группа событий – это совокупность n событий а1, а2, …, Аn, одно из которых обязательно произойдет, т.Е. Свойства операций над событиями
- •Правило двойственности (теорема де Моргана)
- •Алгебра событий.
- •Вероятность. Классическое определение вероятности события
- •Геометрическая вероятность
- •Статистическая вероятность
- •Свойства вероятности
- •Лекция 2 Условная вероятность.
- •Формула вероятности произведения событий (теорема умножения вероятностей). Независимые события
- •Формула вероятности суммы совместных событий (теорема сложения вероятностей)
- •Формула полной вероятности
- •Формула Байеса (теорема гипотез)
- •Лекция 3. Случайные величины
- •Лекция 4 Повторные испытания.
- •Распределения, связанные с повторными испытаниями.
- •Лекция 5
- •Лекция 6. Двумерные случайные величины
- •Свойства функции распределения.
- •Свойства плотности.
- •Свойства коэффициента корреляции.
- •Двумерное равномерное распределение
- •Двумерное нормальное распределение
- •Задача линейного прогноза.
- •Лекция 7. Законы больших чисел и центральная предельная теорема. Неравенства Чебышева.
- •Законы больших чисел.
- •Теорема Чебышева
- •Обобщенная теорема Чебышева.
- •Теорема Маркова.
- •Теорема Бернулли.
- •Предельные теоремы.
- •Теорема Ляпунова.
- •Теорема Леви – Линдеберга.
- •Интегральная теорема Муавра – Лапласа.
- •Лекция 8 Элементы математической статистики
- •Основные задачи статистики.
- •Эмпирические законы распределения.
- •Точечные оценки параметров распределения.
- •Требования к оценкам.
- •2. Несмещенная, состоятельная оценка дисперсии
- •Интервальные оценки.
- •Доверительные интервалы для параметров нормального закона распределения. Доверительный интервал для математического ожидания.
- •Доверительный интервал для среднеквадратического отклонения .
Лекция 7. Законы больших чисел и центральная предельная теорема. Неравенства Чебышева.
Первое
неравенство Чебышева.Пусть случайная
величинаX0
и существует ее математическое ожиданиеM(X). Тогда
для любого>0
выполнено первое неравенство Чебышева![]() .
.
Доказательство. В
дискретном случае
![]() .
.
В непрерывном
случае
![]() .
.
Второе
неравенство Чебышева.Пусть существуют
математическое ожидание и дисперсия
случайной величины![]() .
Тогда для любого
.
Тогда для любого![]() выполнено второе неравенство Чебышева
выполнено второе неравенство Чебышева
![]()
Доказательство проведем для непрерывного случая, для дискретного случая оно доказывается аналогично.
![]()
Последовательность
случайных величин сходится по
вероятности к числу
![]()
![]() ,
если
,
если![]()
Законы больших чисел.
Законы больших чисел могут быть записаны в разных формах, но суть их состоит в том, что при большом числе случайных явлений их средний результат практически перестает быть случайным.
Теорема Чебышева
(Закон больших чисел в форме Чебышева)
При достаточно большом количестве независимыхопытов среднее арифметическое наблюденных значений случайной величины сходится по вероятности к ее математическому ожиданию.
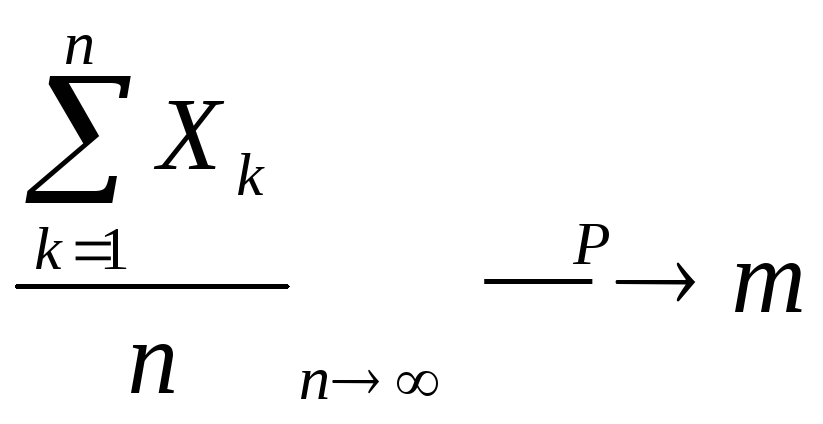 .
.
Доказательство.
Рассмотрим
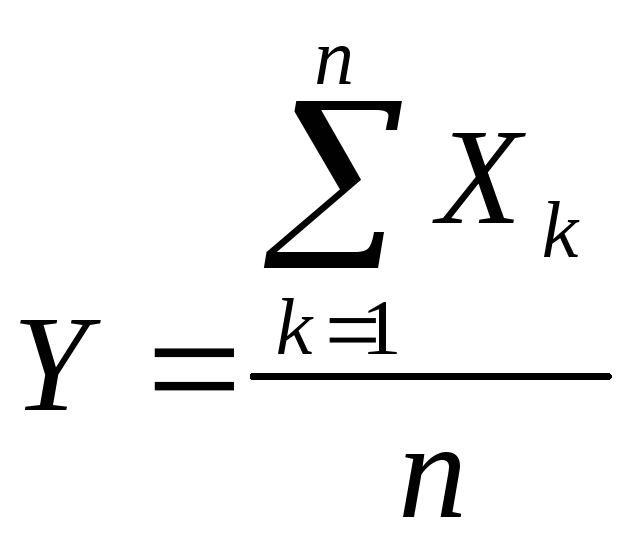 ,
,![]()
![]() .
.
Тогда по второму
неравенству Чебышева
![]() .
.
Если выбрать
![]() ,
(
,
(![]() -
целая часть), то приn>Nбудет
-
целая часть), то приn>Nбудет![]() ,
следовательно, приn>Nбудет выполнено неравенство
,
следовательно, приn>Nбудет выполнено неравенство![]() ,
поэтому при тех же значенияхnбудет
,
поэтому при тех же значенияхnбудет![]() .
.
Следовательно,
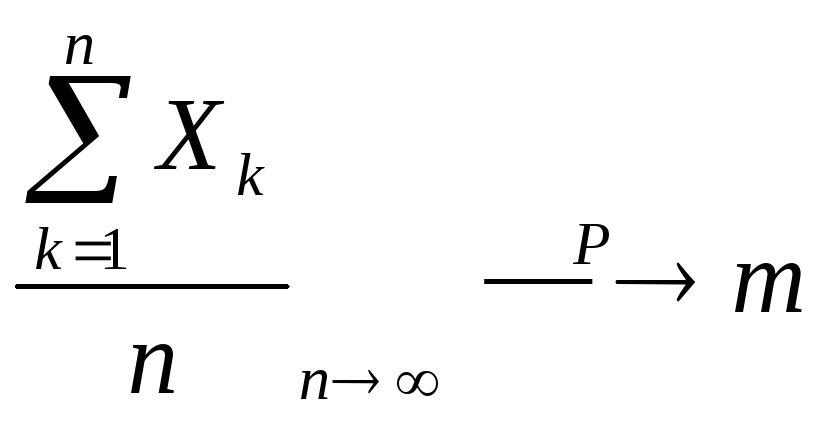 .
Теорема Чебышева доказана.
.
Теорема Чебышева доказана.
Обобщенная теорема Чебышева.
Пусть X1,Xn– независимые случайные величины с математическими ожиданиямиm1,…mn и дисперсиямиD1…,Dn. Пусть дисперсииограничены в совокупности(Dk<L,k-1,2…n). Тогда среднее арифметическое наблюденных значений случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий.
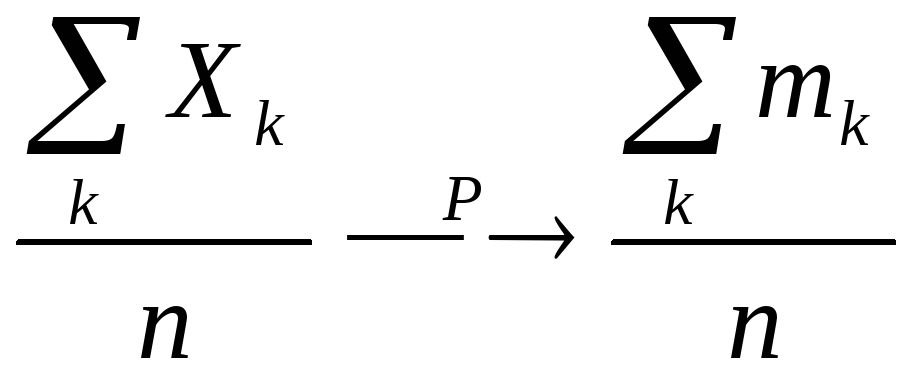
Доказательство.
Рассмотрим, как в предыдущей теореме
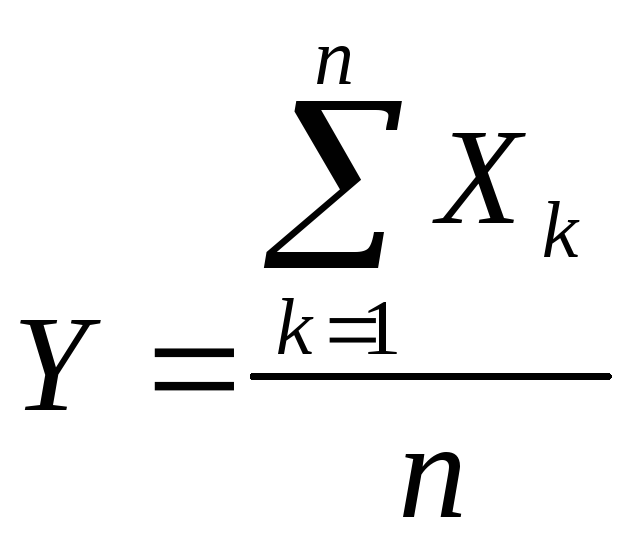 .
.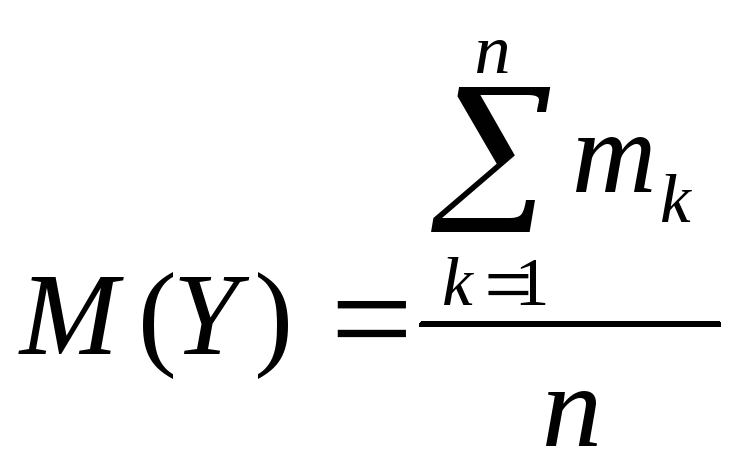 ,
,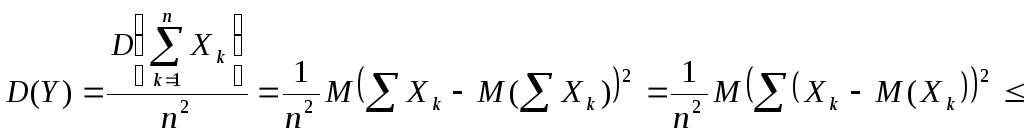
![]() =
=
(случайные величины независимы, следовательно, и не коррелированны)
![]() .
Отсюда по второму неравенству Чебышева
следует утверждение теоремы (доказательство
сходимости по вероятности проводится
как в предыдущей теореме).
.
Отсюда по второму неравенству Чебышева
следует утверждение теоремы (доказательство
сходимости по вероятности проводится
как в предыдущей теореме).
Теорема Маркова.
![]() ПустьX1,Xn–зависимыеслучайные величины с
математическими ожиданиямиm1,…mn
и дисперсиямиD1…,Dn.
Пусть
ПустьX1,Xn–зависимыеслучайные величины с
математическими ожиданиямиm1,…mn
и дисперсиямиD1…,Dn.
Пусть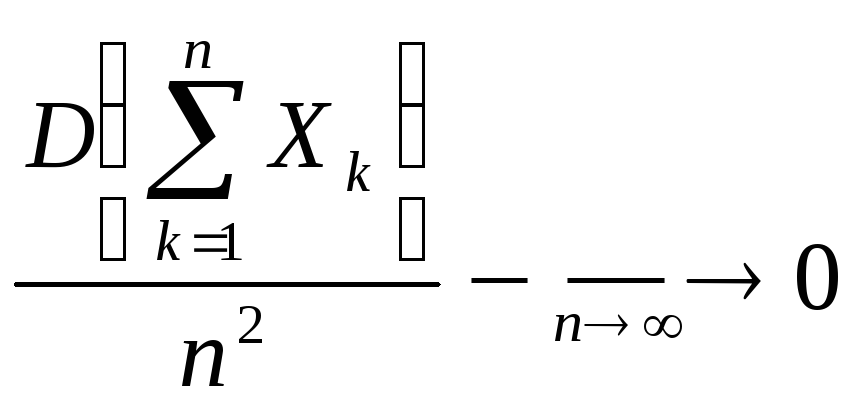 .
Тогда среднее арифметическое наблюденных
значений случайных величин сходится
по вероятности к среднему арифметическому
их математических ожиданий.
.
Тогда среднее арифметическое наблюденных
значений случайных величин сходится
по вероятности к среднему арифметическому
их математических ожиданий.
Доказательство. Доказательство сходимости по вероятности проводится как в теореме Чебышева.
Теорема Бернулли.
При неограниченном увеличении числа опытов – независимых испытаний частота события сходится по вероятности к вероятности события.
Доказательство проводится аналогично теореме Чебышева.
Предельные теоремы.
Центральная предельная теорема– это любая теорема, ставящая условия, при которых функция распределения суммы индивидуально малых случайных величин с ростом числа слагаемых сходится к нормальной функции распределения.
Центральная
предельная теорема подтверждает
следующее: если исход случайного
эксперимента определяется большим
числом случайных факторов, влияние
каждого из которых пренебрежимо мало,
то такой эксперимент хорошо аппроксимируется
нормальным распределением с параметрами
![]() ,
подобранными соответствующим образом.
,
подобранными соответствующим образом.
