
Kvanttyk_mekhanika_1RK
.docКванттық механика
Гамильтон-Якоби кванттық теңдеуі мына түрге ие:
A)&
 .
.
ВКБ (Венсель Крамерса Брюллена) жуықтау әдісі қолданылады егер:
A)& Потенциалдық энергия функция координатына баяу ауысады.
Физикалық өлшемде орташа мәнді мына формула бойынша анықтайды:
A)&
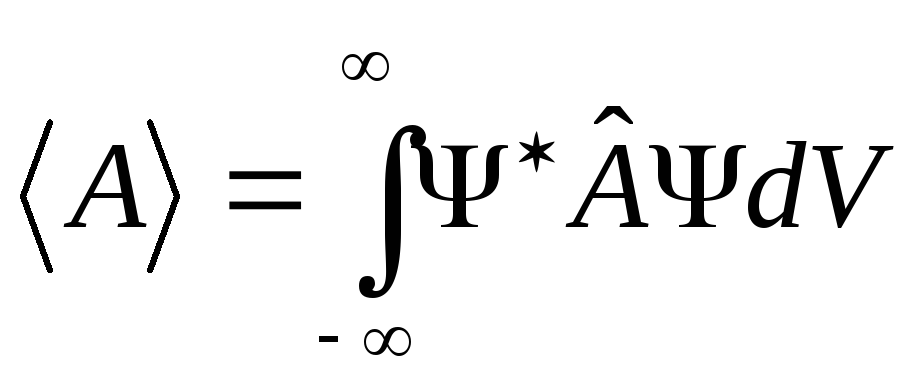 .
.
Физикалық өлшемде орташа мәнді мына формула бойынша анықтайды:
A)&
![]() .
.
Екі физикалық өлшемнің коммутаторы мына формула бойынша анықтайды:
A)&
![]() .
.
Пуасонның кванттық жақшалары мына түрге ие:
B)&
![]() .
.
Электронның спиндік проекциялары мынадай мәндерді қабылдайды:
D)&
![]() .
.
Электронның магниттік спинінің саны мынадай мәндерді қабылдайды:
E)&
![]() .
.
Орбиталды кванттық сан мынадай мәндерді қабылдайды:
A)&
![]() .
.
Сутегі атомындағы электрондардың орбиталдық моменті мынадай мәндерді қабылдайды:
E)&
![]() .
.
Магниттік кванттық сан мынадай мәндерді қабылдайды:
A)&
![]() .
.
Реттеудің іріктеу ережесі:
A)& Энергетикалық деңгейлердің арасындағы рұқсат етілген ауысулар
Импульс көрсетілімінде импульс операторы мына түрге ие:
A)&
![]() көбейткіш ретінде.
көбейткіш ретінде.
Координат көрсетілімінде координат операторы мына түрге ие:
A)&
![]() көбейткіш ретінде
көбейткіш ретінде
Координат көрсетілімінде импульс операторы мына түрге ие:
B)&
![]() .
.
Импульс көрсетілімінде координат операторы мына түрге ие:
C)&
 .
.
Координат көрсетілімінде жүйе күйінің көрсетілімі:
A)&
![]() .
.
Меншікті функцияға есеп, меншікті мән:
A)&
![]() .
.
Бөлшек сандарының сақталу заңы мына түрге ие:
A)&
![]() .
.
Паули теориясында спин операторы мына түрге ие:
A)&
 .
.
Өздік функцияның ортонормировкасының шарты:
A)&
![]() .
.
Өздік функцияның ортонормировка шартының түрі:
A)&
![]() .
.
![]() және
және![]() операторының
кедергілерінің эрмиттік шарты:
операторының
кедергілерінің эрмиттік шарты:
B)&
![]() .
.
Кванттық механиканың құрылуы үшін қандай мәселе игерді:
A)& Абсолюттік қара дененің сәулеленуі.
де- Бройльдің толқынына сәйкесті энергиясы:
A)&
![]()
![]() .
.
де- Бройльдің толқынына сәйкесті жалпы формуласы:
E)&
![]() .
.
де- Бройльдің толқынына сәйкесті жалпы өрнегі:
D)&
![]() .
.
х осі бойымен таралатын де-Бройльдің толқындық өрнегі:
C)&![]() .
.
х осіне қарсы таралатын де- Бройльдің толқыны үшін өрнек:
D)&
![]() .
.
х осі бойымен таралатын де-Бройльдің толқыны үшін өрнекі:
C)&
![]() .
.
х осіне қарсы таралатын де- Бройльдің толқыны үшін өрнек:
B)&
![]() .
.
Элементар бөлшекке сәйкес келетін де- Бройль толқынының жылдамдығы:
A)& жарық жылдамдығынан артық.
Элементар бөлшекке сәйкес келетін толқындық түйдек құраушыларының фазалық жылдамдығы:
A)& жарық жылдамдығынан артық.
Элементар бөлшекке сәйкес келетін толқындық пакетінің (түйдектің топтық жылдамдығы:
D)& бөлшектің жылдамдығына тең
Толқындық пакет (түйдек) теориясы:
A)& Элементар бөлшек үшін толқындық пакет (түйдек) таралатын болғандықтан теория орнықсыз.
Бөлшектердің спинін ескермейтін релятивистік емес кванттық механика кіммен өңделді:
C)& Шредингер и Гейзенбергпен
Бөлшектердің спинін ескеретін релятивистік емес кванттық механика кіммен өңделді:
D)& Паулимен
Бөлшектердің спинін ескермейтін релятивистік кванттық механика кіммен өңделді:
B)& Клейн и Гордонмен.
Бөлшектердің спинін ескеретін релятивистік екванттық механика кіммен өңделді:
A)& Диракпен
Бірінші кванттық теорияны кім ұсынды:
E)& Бор
Толқындық функцияның дұрыс интерпретациясын кім ұсынды
C)& Борн.
Кванттық механиканың
операторлық тұжырымдамасын кім ұсынды:
A)& Шредингер
Кванттық механиканың матрицалықтұжырымдамасын кім ұсынды:
B)& Гейзенберг
Гейзенберг пен Шредингердің кванттық механиканың тұжырымдамасы келесі түрде бір- бірімен қатынасады:
C)& Екі тұжырымдамасы тең құқылы
Шредингердің стационарлық тендеуі:
A)&
![]() .
.
Шредингердің уақыттық теңдеуі:
B)&
![]() .
.
Шредингердің жалпы теңдеуі:
C)&
![]() .
.
Шредингердің уақыттық теңдеуі:
B)&
 .
.
Шредингердің стационарлық теңдеуі:
D)&
![]() .
.
Шредигердің стационарлық теңдеуін келесі жағдайларда қолдануға болады:
B)& Жүйенің потенциалдық энергиясы уақыттан тәуелсіз болса.
Шредингердің уақыттық теңдеуін келесі жағдайларда қолдануға болады:
C)& Әрқашан.
Шредингердің стационарлық пен уақыттық теңдеулерінің дербес шешімдері келесі қатынаспен байланысқан:
A)&
![]() .
.
Гейзенбергтің
анықталмағандық принципі (мұндағы
![]() ,
,
![]() - орташа квадраттық ауытқулар):
- орташа квадраттық ауытқулар):
A)&
![]() .
.
Гейзенбергтің анықталмағандық принципі келесі түрге ие:
A)&
![]() .
.
Суперпозиция принципі:
A)&
Егер
жүйе
![]() мен
мен
![]() күйлерде
орналасатын болса, онда ол
күйлерде
орналасатын болса, онда ол
![]() күйлерде болуы мүмкін,
мұндағы
күйлерде болуы мүмкін,
мұндағы
![]() ,
,
![]() - комплекстік тұрақтылар.
- комплекстік тұрақтылар.
Толқындық функцияның нормалау шарты келесі түрге ие:
A)&
![]() .
.
Толқындық функцияның нормалау шарты келесі түрге ие:
A)&
 .
.
Еркін бөлшектің толқындық функциясы:
E)&
![]()
де-
Бройльдің қатынасы бөлшектің корпускулярлық
![]() және
және![]() арасындағы
байланысты қалыптастырады және келесі
тұжырымды:
арасындағы
байланысты қалыптастырады және келесі
тұжырымды:
D)&
![]() ,
,
![]() .
.
Эрмиттік оператордың өздік мәндері .... бола алмайды
C)& комплексті сандар
Гармоникалық осциллятордың энергия спектрі … болып табылады:
A)& Эквидистантты.
Кванттық механикада физикалық өлшемге сәйкесінше қойылады:
D)& Сызықты эрмитті оператор.
Бөлшектің
кинетикалық энергиясының операторы
координатты келесі түрге ие (![]() -
Лаплас операторы):
-
Лаплас операторы):
D)&
![]() .
.
Физикалық мағынасы жоқ:
D)& Гамильтон операторының өздік теріс мәндері.
Сутекті атомдағы бөлшектің энергетикалық спектрі:
E)& Дискретті энергия өсімшесімен үйлеспейді, кейін үзіліссіз.
А және В физикалық шамалар бірдей өлшенді.
Бұл мына шаманы білдіреді:
C)&
![]() .
.
Поправка первого порядка к энергии невырожденного уровня в теории возмущений равна:
D)& Нәтижелі қоздыру энергиясының орташа мәніне.
Эрмиттік оператордың өздік мәндері болып табылады (жалпы жауапты табыңыз):
B)& Заттық сандар.
![]() күйі
және F
физикалық шамасы берілген.
Осы
шаманы өлшегенде қай кезде бір мәнді
алады?:
күйі
және F
физикалық шамасы берілген.
Осы
шаманы өлшегенде қай кезде бір мәнді
алады?:
E)& Егер күй F операторына қатысты өздік болса.
Координаттар мен импульс проекциялары үшін коммутацилық қатынастар келесі түрге ие:
E)&
![]() .
.
Операторлардың қайсысы өздік функциялардың жалпы жүйесіне ие?:
A)& Импульс моменті квадратының операторы және оның проекцияларының біреуі.
Эрмитті оператордың өздік функциясы:
A)& Толық функциялар жиынтығын құрайды.
Паули матрицалары келесі коммутациялық қатынастарды қанағаттандырады:
E)& Импульс моментінің крмпоненттері.
Паули теңдігі Шредингер теңдігіне қосымша ... ескереді::
A)& Электрон спинін.
Қоздыру теориясы қоздыру өрісі... болғанда қолданылады:
C)& Қозбаған өрістің мәнінен көпке аз.
Операторды ... деп түсінеміз:
B)& Бір функциядан басқасын алатын кейбір әрекеттер.
Өздік мәндер спектрін азған деп атайды, егер:
A)& Бір өздік мәнге өздік функциялар қатары сәйкес келсе..
Физикалық шаманың әр нақты өлшемі кезінде:
A)& Сәйкес оператордың өздік мәндерінің мүмкін мәндерінің бірін аламыз.
Физикалық шамаларға сәйкес келетін операторлар міндетті түрде:
E)& Сызықты және эрмитті.
Оператордың
сызықты шарты
![]() (A=const, B=const):
(A=const, B=const):
B)&
![]() .
.
Импульстік негіздегі толқындық функция:
A)&
Импульс
операторының
өзіндік
функциясы
бойынша
![]() бөлу коэффициенттерімен
анықталады.
бөлу коэффициенттерімен
анықталады.
Энергетикалық негіздегі толқындық функция:
B)&
Гамильтон
операторының
өзіндік
функциясы
бойынша
![]() бөлу коэффициенттерімен
анықталады.
бөлу коэффициенттерімен
анықталады.
Гармоникалық осциллятордың өзіндік функциясы келесі негіз арқылы көрінеді:
C)& Эрмит полиномдары арқылы.
Орталық-симметриялық аймақта бөлшектердің энергетикалық спектрі дискретті спектрін бейнелейді егер:
C)&
Бөлшек
энергиясы
![]() <
0.
<
0.
Кванттық механикадағы әрбір бақыланатын физикалық шама көрсетіледі:
A)& Желілі эрмиттік оператормен.
Сипатталатын
функция жағдайындағы бақыланатын
физикалық шаманың орташа мәні
![]() :
:
E)&
![]() .
.
Дирактық
көзқарастағы сипатталатын функция
жағдайындағы бақыланатын физикалық
шаманың орташа мәні
![]() :
:
B)&
![]() .
.
Кванттық механикадағы суперпозиция қағидасы жауап береді:
A)& Оператордың сызықтылығына.
Эрмиттердің
сызықтық
операторы
A
егер
![]() және
және
![]() кез-келген функциясы үшін шарты орындалса:
кез-келген функциясы үшін шарты орындалса:
A)![]()
Эрмиттер
сызықтық операторы егер
![]() және
және
![]() кез-келге функциясы үшін қатынас
орындалса:
кез-келге функциясы үшін қатынас
орындалса:
D)&![]()
Егер
А операторы
![]() функцияны тек сандық көбейткіштен
ажырататын
функцияны тек сандық көбейткіштен
ажырататын
![]() функцияға көшірсе онда:
функцияға көшірсе онда:
A)&
![]() функциясы
А операторының өзіндік функциясы.
функциясы
А операторының өзіндік функциясы.
![]() операторының
өзіндік функциясы тең:
операторының
өзіндік функциясы тең:
B)&
![]() .
.
![]() операторының
өзіндік мәні:
операторының
өзіндік мәні:
C)& Заттың сандық осінің кез-келген мәнін қабылдауы мүмкін.
Шредингердің стационарлы теңдігі:
D)& Гамильтон операторының өзіндік мәніне теңдеуі бар.
Шредингердің стационарлы теңдеуі:
E)& Гамильтон операторының өзіндік мәніне теңдеуі бар.
![]() элементі
бар матрица тапсырады:
элементі
бар матрица тапсырады:
A)&
![]() функция базисінде В операторын ұсынады.
функция базисінде В операторын ұсынады.
Сутегі атомының энергетикалық спектрі мынадай сипатта болады:
E)& Кейбір мәнге дейін дискретті сипатта.
Сутегі атомы үшін Гамильтон операторының өзіндік мәнінің спектрі:
E)& Туындау деңгейі басты квантты санға байланысты.
Магнитті квантті сан өзіндік мәнді анықтайды:
B)& Импульс кезіндегі проекция операторын.
Сутегі атомы үшін орбитальды квантты сан мынадай мәнді қабылдайды:
C)&
![]() .
.
