
основы меаллургических процессов
.pdfвещества A к веществу B (например, мерой химического сродства металла к кислороду).
Температурная зависимость стандартной GoT определяется, как это было показано выше, путем интегрирования:
|
|
|
|
|
|
T |
|
|
|
T |
C |
|
|
|
Go |
Ho |
|
|
|
C |
dT T So |
|
|
T |
P |
dT , |
|
|
|
|
|
|
|
||||||||
|
|
T |
298 |
|
|
P |
298 |
|
|
|
|
|
|
|
|
|
|
|
|
298 |
|
|
|
298 |
|
|
|
где C |
, Ho |
, So |
– |
алгебраическая |
|
сумма теплоемкостей, |
|||||||
P |
298 |
|
298 |
|
|
|
|
|
|
|
|
|
|
стандартные значения энтальпии и энтропии веществ, участвующих в реакции.
Если величина CP связана с температурой выражением вида:
CP a b T c T 1 ,
где a, b, c – справочные величины, то для реакции (4.1) будет:
GoT A B Tln T B T 1 C T ,
где A', B', B", C = const.
Погрешность экспериментального определения величины менее ±2000 Дж/моль считается удовлетворительной для многих металлургических реакций, поэтому в справочной литературе температурная
зависимость GoT f T часто представлена уравнениями:
GoT A B Tln T C T (для случая линейной зависимости CP f T );
GoT A C T (для случая независимости CP от температуры).
71
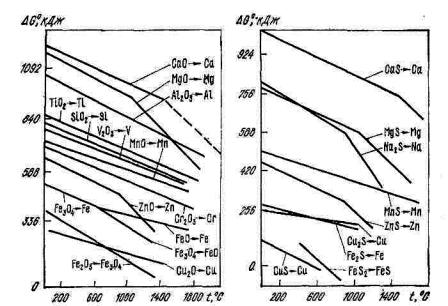
Рис. 4.1. Зависимость стандартной энергии Гиббса Gº диссоциации оксидов от температуры (на 1 моль кислорода)
Рис. 4.2. Зависимость стандартной энергии Гиббса Gº диссоциации сульфидов от температуры (на 1 моль серы)
На рисунках 4.1, 4.2 представлена зависимость GoT f T для
реакций диссоциации оксидов и сульфидов. Можно отметить, что зависимости имеют сходный характер изменения. Наиболее прочными являются соединения с большей величиной энергии Гиббса GoT . Однако с увеличением температуры уменьшение химической прочности (уменьшение GoT ) может привести к изменению относительной (по отношению к другому соединению) прочности, и при этом возможно
пересечение линий GTo f T . Линейная зависимость |
GTo f T |
может иметь изломы при температурах, которые совпадают с точками фазовых превращений компонентов. Часто в справочной литературе
приводятся зависимости GoT f T для реакций образования (оксидов,
сульфидов и т.д.), которые графически являются симметричными относительно оси температур графикам, приведенным на рисунках 4.1, 4.2.
Анализ прочности соединений с использованием упругости диссоциации pB возможен в случае, когда газ B сам не диссоциирует. Если он диссоциирует, то величина pB, как мера прочности, не характеризует природу оксида; в этом случае необходим полный анализ состава газовой фазы.
72
4.2. Газообразная диссоциация
Существует два вида диссоциации: газообразная и конденсатная. В случае газообразной диссоциации для продуктов реакции (4.1)
выполняется соотношение p |
A |
po , где |
p |
A |
,po |
– давление паров и |
|
A |
|
A |
|
||
насыщенных паров компонента A, поэтому |
|
|
|
|
||
ABK AГ B. |
|
|
|
(4.4) |
||
Константа равновесия связана с парциальными давлениями |
||||||
продуктов реакции и имеет вид: |
|
|
|
|
|
|
KP pApB . |
|
|
|
(4.5) |
||
Число степеней свободы: C = 2 + 2 – 2 = 2.
Равновесный состав газовой фазы предполагает определение четырех переменных p, T, pA, pB и в одном из простых случаев (температура и давление заданы, а газовая фаза состоит из A и B) необходимо решить два уравнения:
KP pApB ; |
p pA pB . |
Однако часто на практике вещества A и B сами диссоциируют, например, при диссоциации оксидов молекулярный кислород O2 при высоких температурах превращается в атомарный O2 = 2O.
Таким образом, в газовой фазе появляются новые компоненты, и процессы ее формирования связаны со многими превращениями.
Вкачестве примера можно рассмотреть диссоциацию оксида алюминия. В газообразных продуктах диссоциации обнаружено семь
различных веществ: O, O2, Al, Al2, AlO, Al2O, Al2O2. Однако количество Al2 мало, поэтому состав газовой фазы может быть рассчитан по шести компонентам.
Если температура системы варьируется, то можно определить семь переменных (шесть – состав и общее давление) как функцию температуры.
Вкачестве первого уравнения можно использовать связь общего давления с парциальными давлениями веществ, составляющих газовую фазу:
73
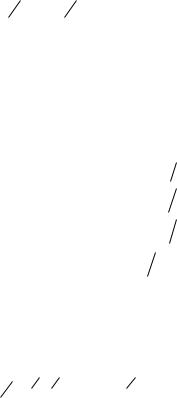
p pO |
pO |
2 |
pAl |
pAlO |
pAl |
O |
pAl |
O |
. |
(4.6) |
|
|
|
|
2 |
|
2 |
|
2 |
|
Второе уравнение связано со стехиометрией исходного оксида:
3 pAl 2 pO ; |
(4.7) |
где pAl pAl pAlO 2pAl2O |
2pAl2O2 ; |
pO pO 2pO2 pAlO pAl2O 2pAl2O2 .
Таким образом,
p |
O |
2p |
O |
|
3 |
p |
Al |
1 |
2 |
p |
AlO |
2p |
Al |
O |
p |
Al |
O |
. |
(4.8) |
|
|
2 |
2 |
|
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
Поскольку в рассматриваемой системе устанавливаются частные равновесия, то можно использовать пять уравнений частных равновесий, для которых имеются экспериментальные данные:
Al O 2Al |
Г |
3O ; |
|
K p2 |
p3 |
; |
|
|
|
|
|
|
|
(4.9) |
||||||||||||||||
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
1 |
Al |
|
|
|
O |
|
|
|
|
|
|
|
|
|
|||
AlOГ AlГ O ; |
|
|
K2 pAlpO |
pAlO ; |
|
|
(4.10) |
|||||||||||||||||||||||
Al |
O |
Г |
2Al |
Г |
O ; |
|
|
K |
3 |
p2 |
p |
O |
p |
Al |
O |
; |
|
|
|
(4.11) |
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Al |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Al |
O |
2 Г |
2Al |
Г |
2O ; |
|
K |
4 |
p2 |
p2 |
|
p |
|
|
|
; |
|
|
|
(4.12) |
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
Al |
|
|
O |
|
Al2O2 |
|
|
|
||||||||||
O |
2 |
2O ; |
|
|
|
|
|
|
|
|
K |
5 |
p2 |
|
p |
O |
. |
|
|
|
|
|
|
|
(4.13) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Решая совместно уравнения (4.8)–(4.13) относительно pO, можно |
||||||||||||||||||||||||||||||
получить: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p3 |
|
2 |
|
|
p4 |
3 |
K 12 p12 |
|
K1 |
p3 2 |
2K1 |
|
|
K1 |
p |
|
. |
(2.14) |
||||||||||
|
|
|
|
|
|
|
|
|
O |
|||||||||||||||||||||
|
|
|
|
O |
|
K5 |
|
|
O |
2 |
1 O |
|
2K2 |
O |
|
|
K3 |
|
|
K4 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Состав газовой фазы как функции температуры представлен в таблице 4.1.
74
Таблица 4.1
Состав газовой фазы и константы равновесия в зависимости от температуры
|
Температура T, K |
|
Температура T, K |
|||||
Показатели |
|
|
|
Показатели |
|
|
|
|
1000 |
2000 |
3000 |
1000 |
2000 |
3000 |
|||
|
|
|||||||
|
|
|
|
|
|
|
|
|
Состав, |
|
|
|
|
|
|
|
|
%: |
|
|
|
Константы |
|
|
|
|
Al |
40,00 |
38,76 |
28,04 |
равновесия: |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
O |
60,00 |
57,53 |
50,17 |
–lgK1 |
119,910 |
40,371 |
14,787 |
|
|
|
|
|
|
|
|
|
|
O2 |
3,0·10-3 |
1,29 |
5,53 |
–lgK2 |
19,546 |
6,668 |
2,340 |
|
AlO |
1,7·10-3 |
1,78 |
8,54 |
–lgK3 |
41,279 |
14,393 |
5,388 |
|
Al2O |
7,6·10-6 |
0,63 |
7,39 |
–lgK4 |
61,120 |
20,460 |
6,900 |
|
Al2O2 |
6,0·10-10 |
0,007 |
0,33 |
–lgK5 |
19,613 |
6,355 |
1,898 |
|
Равновесное парциальное давление алюминия значительно ниже, чем давление насыщенных паров алюминия при соответствующей температуре, поэтому диссоциация имеет газовый характер. Вышеприведенный расчет основан на конгруэнтном характере диссоциации, т.е. выполнении балансового уравнения (4.7). Для газообразной диссоциации характерно влияние вакуума на температуру начала диссоциации соединения. Известно, что изменение энергии Гиббса для реакции (4.4) может быть получено на основе стандартной
величины |
Go |
|
и |
|
поправки на |
переход |
A |
К |
A |
Г |
, |
т.е. |
|
T |
|
|
|
|
|
|
|
|
|
||
G Go RTln p |
A |
( p |
A |
– парциальное давление A в газовой фазе). |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
Установление равновесия ( G 0) |
реакции (4.4), таким образом, |
|||||||||||
регулируется величиной pA , а так как |
pA p pB |
(p – давление в |
||||||||||
системе), то и внешним давлением. |
|
|
|
|
|
|
|
|||||
В ряде случаев при диссоциации |
pA pB , тогда |
pA p |
(если |
|||||||||
p pA pB ), то можно считать, что |
|
|
|
|
|
|
|
|||||
G Go RTln p .
Поскольку p < 1, то второе слагаемое правой части меньше нуля, и при вакуумировании системы равновесие реакции (4.4) может быть достигнуто при различных температурах в зависимости от величины p.
75

При диссоциации оксида магния 2MgO 2Mg O2 , магний может
находиться в парообразном состоянии в обычных условиях pMg ≥ 1, если
T > 1368 K. Таким образом, при T = 2500 K 2MgOK 2MgГ O2 .
Стандартное изменение энергии Гиббса для этой реакции имеет
вид:
Go 1518 0,061Tlg T 0,633T кДж .
Константа равновесия (если не учитывается диссоциация молекулярного кислорода) равна KP p2MgpO2 .
При учете балансового уравнения pMg 2pO2 .
Парциальное давление кислорода представлено выражением:
|
|
|
|
K |
P |
|
|
|
8 0,9 10 19 |
|
||
p |
|
3 |
|
|
3 |
|
|
5,87 10 7 , |
||||
O |
4 |
4 |
||||||||||
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
парциальное давление магния выражается
pMg 2pO2 1,16 10 6 .
Таким образом, при pMg < 1,16·10-6 происходит газообразная конденсация, температуру начала которой можно регулировать величиной p.
4.3. Конденсатная диссоциация
Если для реакции (4.1) pA poA , то вещество A находится в конденсированном состоянии и происходит конденсатная диссоциация:
ABK AК B. |
(4.15) |
Как было отмечено выше, константа равновесия в случае чистых фаз AB и A будет равна KP = pB, то есть упругости диссоциации:
pB exp( GoT / RT) .
76

Термодинамические характеристики реакции (4.15) зависят от температуры, фазового состояния конденсированных веществ, степени дисперсности твердых фаз, растворимости конденсированных фаз (взаимной и в других, нейтральных веществах). Температурная зависимость pB в координатах pB–T представлена на рисунке 4.3.
Рис. 4.3. Зависимость упругости диссоциации соединения от температуры: I – область устойчивого существования AB; II – область устойчивого существования A
Поле диаграммы линией равновесных значений pB разделяется на две области. Для области I (точка 1) давление газа B выше равновесного, поэтому для этой области характерно устойчивое существование соединений AB. Для области II (точка 2) вследствие того, что давление газа B ниже равновесного, устойчиво существует вещество A, поэтому направление реакции (4.15) в области значений I – слева направо, в области II – справа налево.
Сравнение равновесных pO2 для нескольких оксидов (см. рис. 4.4)
показывает, что, с одной стороны, можно определить их взаимную прочность (оксид FeO прочнее оксида Ag2O), с другой стороны, можно определить температуру, при которой эти оксиды диссоциируют на воздухе (если pO2 = 0,021 МПа).
Рис. 4.4. Сравнение химической прочности некоторых оксидов: 1 – Ag2O; 2 – CuO; 3 – Fe2O3; 4 – Cu2O; 5 – PbO; 6 – NiO; 7 – Fe3O4; 8 – FeO
77
Влияние фазовых превращений можно оценить при анализе величины изменения энтальпии H для реакции (4.15). Фазовые превращения (агрегатные, структурные) влияют на прочность оксидов. Если диссоциация происходит при низких температурах, то AB и A могут быть в твердом состоянии:
ABТ AТ B ; Ho HoB HoA HoAB ,
где H° – изменение энтальпии для веществ в стандартном состоянии. При повышении температуры, если TAпл TABпл , то при TAпл вещество
A переходит в жидкую фазу. Тогда
ABТ AЖ B; Ho HoB HoA HплA HoAB ,
где HплA – изменение энтальпии вещества A при его плавлении.
При более высокой температуре, когда плавится (при TABпл ) вещество AB ( p pплAB ),
ABЖ AЖ B ; Ho HoB HoA HплA HoAB НплAB ,
где НплAB – изменение энтальпии вещества AB при его плавлении.
Таким образом, в точках температуры, соответствующих точкам плавления, изменение энтальпии происходит скачкообразно.
Известно, что константа равновесия связана с изменением энтальпии формулой:
ln KP / T Ho / RT2 .
Последнее уравнение можно представить несколько иначе:
|
P |
|
Ho |
|
T |
|
, |
|
T |
R |
T2 |
||||
|
|
|
|
||||
так как KP = pB. |
|
|
|
|
|
|
|
Видно, что кривая pB f (T) |
|
в |
точках изменения фазового |
||||
состояния конденсированных веществ претерпевает изломы, то есть касательная в точке фазового перехода изменяет угол наклона (рис. 4.5) скачкообразно.
78

Рис. 4.5. Влияние фазовых превращений на упругость диссоциации
При дальнейшем увеличении температуры, в точках кипения компонентов (AB или A) наблюдаются дополнительные изломы зависимости pB f (T) .
Так, при диссоциации твердого оксида CdO при |
температуре |
T = 594 K происходит плавление кадмия и при T = 1039 K – его |
|
кипение. Соответственно в этих точках зависимость Go |
f (T) также |
T |
|
имеет изломы.
Таблица 4.2
Энергия Гиббса реакции диссоциации оксида кадмия в зависимости от температуры для разных агрегатных состояний
|
Реакция |
|
|
|
|
|
|
|
Go |
при T, K, кДж |
|
|
|||||
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
400 |
|
594 |
800 |
900 |
|
1039 |
1200 |
|
CdO Cd |
T |
1 |
2 |
O |
2 |
225,72 |
|
203,57 |
– |
– |
|
– |
– |
||||
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
CdO |
T |
Cd |
Ж |
12 O |
2 |
– |
|
203,57 |
177,65 |
165,11 |
|
147,55 |
– |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
CdO |
T |
Cd |
Г |
12 O |
2 |
– |
|
– |
– |
– |
|
147,55 |
114,53 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
В точке плавления кадмия излом pO |
f (T) незначителен. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Влияние изменения степени дисперсности твердых веществ на |
|||||||||||||||
реакционную способность оценивается величиной: |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
GS SdT Vdp , |
|
|
|
|
|||
где GS – изменение энергии Гиббса, обусловленное дисперсностью. |
|||||||||||||||||
|
|
Для индивидуального вещества общий объем V = VM (мольный |
|||||||||||||||
объем) и при T |
|
= const |
GS VM p , |
где |
p – разность давлений |
||||||||||||
внутри тела с изогнутой и плоской поверхностями. Величина p определяется из условия:
79
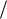
F pdV dS 0 ,
где F – изменение энергии Гельмгольца; ζ – поверхностная энергия.
Из последнего уравнения можно получить p ( dS) dV |
и для |
||
сферической частицы (радиус сферы r) p (2 / r) . Знак |
плюс |
||
определяется кривизной поверхности частицы. |
|
||
Таким образом, для сферической частицы |
|
||
GS (2 VM / |
|
) . |
(4.16) |
r |
|||
Если химическую реакцию, определяемую уравнением (4.1), представить как
AB I A B; AB II A B ,
где AB I и AB II – недиспергированное и диспергированное вещество AB, соответственно, то
GSo GoII GoI ,
где GSo – стандартное изменение энергии Гиббса при диспергировании
вещества AB. Очевидно, что
GSo RTln KI 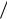 KII .
KII .
В общем случае величина GSo учитывает дисперсность в виде
уравнения (4.16) для всех твердых веществ – участников реакции с соответствующим знаком. Так, для реакции диссоциации карбоната
кальция CaCO3 CaO CO2 при |
|
изменении |
дисперсности обеих |
|||||||||
твердых фаз величина Go равна: |
|
|
|
|
|
|
|
|
|
|
||
|
|
S |
|
|
|
|
|
|
|
|
|
|
Go |
Go |
Go |
|
|
2 CaOVCaO |
|
2 CaCO3 VCaCO3 |
. |
||||
S |
S(CaO) |
S(CaCO |
) |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
rCaO |
|
rCaCO3 |
||||
|
|
|
|
|
|
|
||||||
Однако чаще всего есть возможность регулирования |
||||||||||||
дисперсностью CaCO3 |
(например, |
измельчение в мельницах). В этом |
||||||||||
80
