2.6 Магнит өрісінің энергиясы және оның көлемдік тығыздығы

Тогы бар өткізгіш ылғи да магнит өрісінің қоршауында болады, магнит өрісі токтың пайда болу және жоғалуына байланысты. Магнит өрісі электр өрісі сияқты энергия сақтаушысы болып табылады. Магнит өрісін туғызу үшін ток энергиясының бөлігі жұмсалады, сондықтан магнит өрісінің энергиясы токтың осы өрісті тудыру үшін жұмсалған жұмысына тең деген болжам айтуға болады. Бойымен І тогы жүретін контурды қарастырайық. Контурдың индуктивтілігі L болсын. Егер контурдағы ток dІ-ге өзгерсе, онда онымен ілініскен ағын dФ=LdІ-ге өзгереді, ал мұнда істелінген жұмыс dА= dФ=L dІ болады. Ф ағыны пайда болуға қажетті жұмыс:

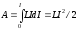(2.24)

болады. Контурмен байланысқан магнит өрісінің энергиясы:

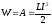. (2.25)

Енді ұзын соленоидтың ішіндегі біртекті магнит өрісінің энергиясын есептейік.

L = ₀ n² V, B = ₀Н, Н = nІ

екені белгілі.

L мен І-дің мәндерін (2.25)-ке қоятын болсақ:

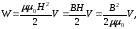(2.26)

мұндағы V = Sl – соленоид көлемі.

Энергия соленоид ішіне топтасқан және тұрақты көлемдік тығыздықпен 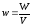таралған болады. Сонымен,

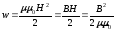. (2.27)

Нег. 2 [ 181-198], 7 [275-288], 8 [ 223-235].

Қос. 22 [206-233], 48 [ 217-235].

Бақылау сұрақтары:

1. Электромагниттік индукция заңы мен энергияның сақталу заңының арасында қандай байланыс бар?

2. Өткізгіш контурының индуктивтігі және екі контурдың өзара индуктивтігінің физикалық мәні қандай?

3. Полярлы молекулалары бар парамагнетиктің магниттелуі мен диэлектрлік поляризациялануын қалай салыстыруға болады?

4. Заттың магниттік күйінің сандық сипаттамасын қандай шама атқарады?

5. Ферромагнетиктердің магниттік қасиеттерінің ерекшеліктері қандай?

3 Дәріс

Максвелдің теңдеулер жүйесі. Электромагниттік тербелістер

3.1 Максвелдің бірінші теңдеуі

Фарадей ашқан электромагниттік индукцияның негізгі заңы бойынша ЭҚК:

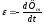, (3.1)

мұндағы Ф_m – магнит индукциясының ағыны. Ол өз кезінде төмендегідей формула бойынша анықталады:

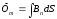, (3.2)

мұндағы S – тұйық контурдың ауданы; В_n – магнит индукциясы векторы В-ның ауданға нормаль 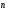-ге проекциясы. Тұрақты ток бөлімінде келтірілген анықтама бойынша тұйық контурдағы ЭҚК:

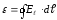, (3.3)

мұндағы 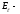электр өрісі кернеулік векторының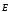контур элементі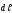бағытына проекциясы.Келтірілген (3.1) және (3.3) теңдеулердің оң жақтарын өзара теңестіретін болсақ, онда (3.2) ескере отырып алатынымыз:

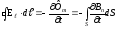. (3.4)

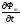–дербес туынды магнит индукциясының ағынының тек уақытқа тәуелділігін көрсетеді.

Алынған (3.4) соңғы теңдеуден магнит өрісінің өзгерісі, айнымалы электр өрісінің пайда болуының себепшісі екені байқалады. Кернеулік векторының циркуляциясы нөлден өзгеше, демек бұл магнит өрісі қоздырған электр өрісі, потенциалды өріс емес, құйынды өріс екендігін дәлелдейді. Құйынды өрістің күш сызықтары тұйық және олардың кеңістікте өткізгіштің бар-жоғына байланыссыз-ақ пайда болатындығын көрсетеді. Аталған (3.4) теңдігінің негізінде Максвелл осындай қортындыға келді. Сондықтан (3.4) өрнегі Максвелдің интегралдық түрдегі бірінші теңдеуі деп аталады.