1. Матрицы и их виды.

Прямоугольная матрица размеров m  n (m  n) как известно, записывается в виде

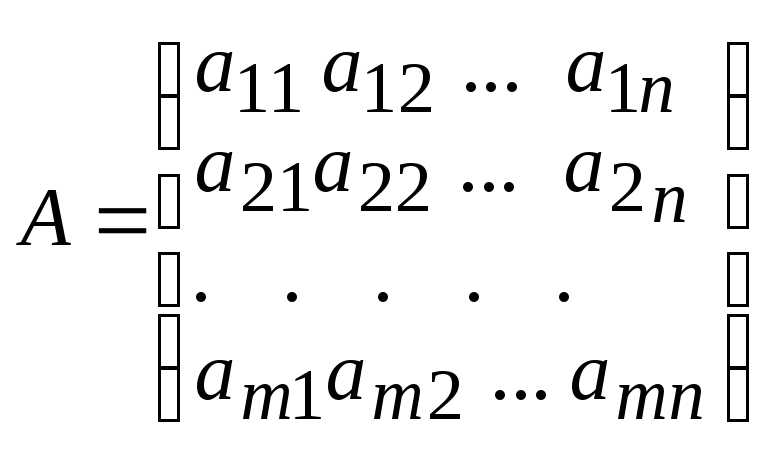. (3)

При т = 1 матрица (3) имеет вид: и на-зывается м а т р и ц е й - с т р о к о й или в е к т о р - с т р о- к о й. При п = 1 матрица имеет вид: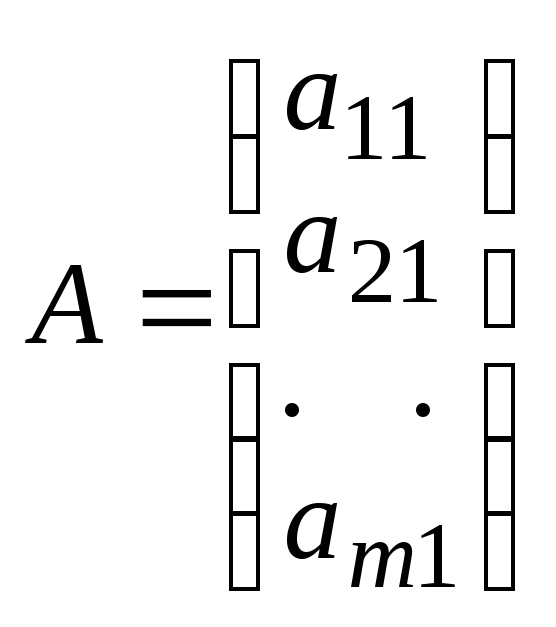

и называется м а т р и ц е й - с т о л б ц о м или в е к т о р - с т о л б ц о м.

При т = п из (3) получаем к в а д р а т н у ю матрицу п-го порядка

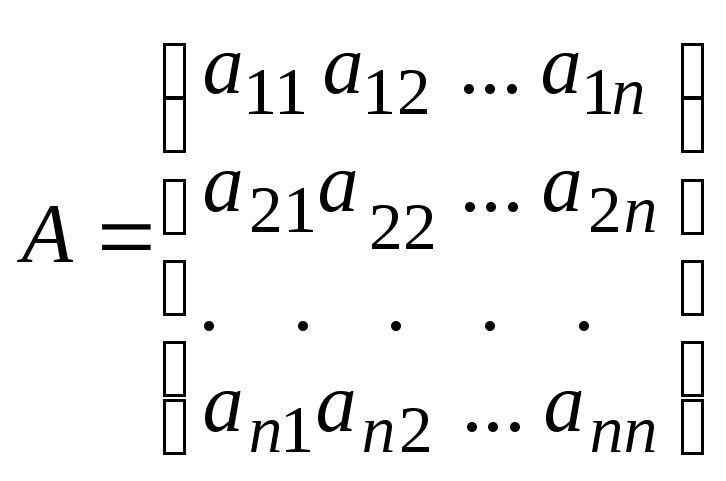. (4)

Говорят, что элементы а₁₁,а₂₂, … , а_nn составляют г л а в н у ю д и а г о н а л ь матрицы А, элементы а_ij, i  j называют в н е- д и а г о н а л ь н ы м и.

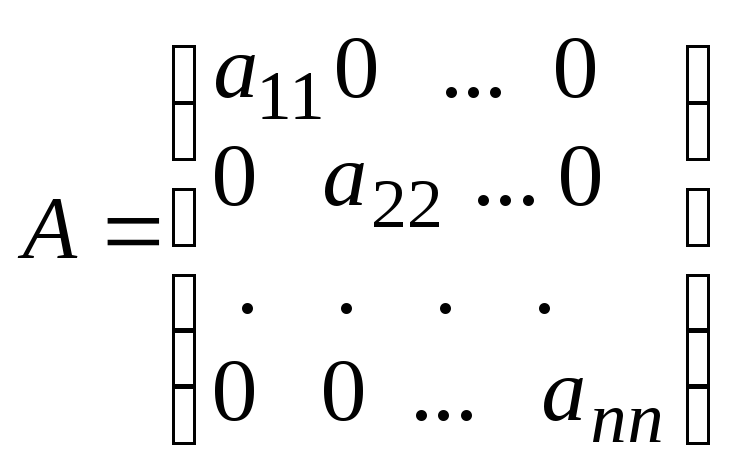
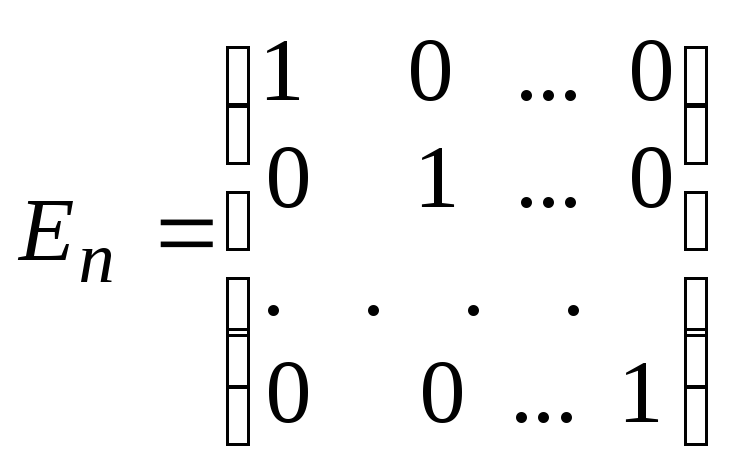
Квадратная матрица, все внедиагональные элементы которой равны нулю, называется д и а г о н а л ь н о й. Если , то она называется е д и н и ч н о й.

.

Квадратная матрица называется т р е у г о л ь н о й, если равны нулю все ее элементы, стоящие ниже (или выше) главной диагонали. Например, треугольной является матрица

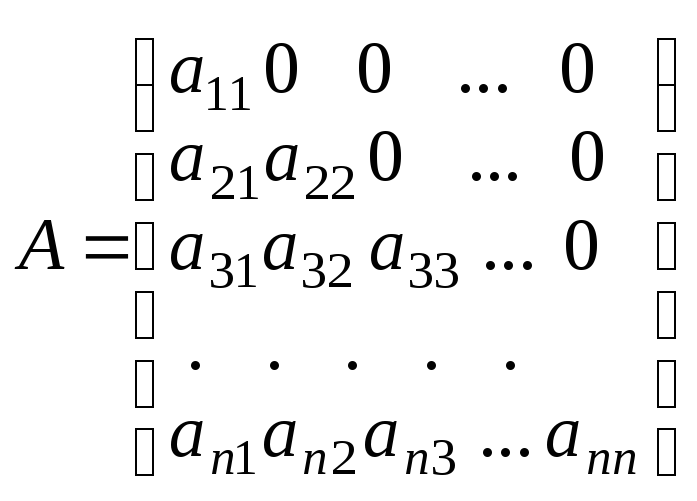или

Если определитель , то квадратная матрица (4) называется н е в ы р о ж д е н н о й или н е о с о б е н н о й, а если , то квадратная матрица (6) называется в ы р о ж д е н н о й или о с о б е н н о й.

Матрица (не обязательно квадратная) все элементы которой равны нулю, называется н у л ь - м а т р и ц е й или н у л е -в о й матрицей и обозначается символом О.

Линейные операции над матрицами.

С у м м о й А+В двух прямоугольных матриц А и В одинаковой размерности называется такая матрица С той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц А и В, т.е. .

П р о и з в е д е н и е м м а т р и ц ы А н а ч и с л о называется матрица А, полученная умножением на всех эле-ментов матрицы А, т.е. а^_ij =  а_ij.

Операции сложения, вычитания матриц и умножения матрицы на число называются л и н е й н ы м и.

Умножение матриц и его свойства.

П р о и з в е д е н и е м матрицы размеров т п на матрицу размеровn  q называется такая матрица размеров т q, элементы c_ik которой равны скалярному произведению i-ой строки матрицы А на k-й столбец матрицы В, т.е.

.

Заметим, что умножение матриц определено тогда и только тогда, когда число столбцов первого множителя равно числу строк второго множителя (в частности, произведение квадратных матриц существует, если они одного порядка). Размерности строк и столбцов матриц-сомножителей и матрицы-произведения подчинены следующей схеме:

m  n

n  q

m  q

 =

Произведение матриц зависит, вообще говоря, от порядка сомножителей, т.е. не обладает в общем случае свойством переместительности.

Заметим, что хотя матрицы А  В и В  А, вообще говоря, не равны, но их определители всегда равны, т.к. определитель матрицы-произведения равен произведению определителей перемножаемых матриц, т.е. , где А и В квадратные матрицы одного и того же порядка.

Пусть в матрице 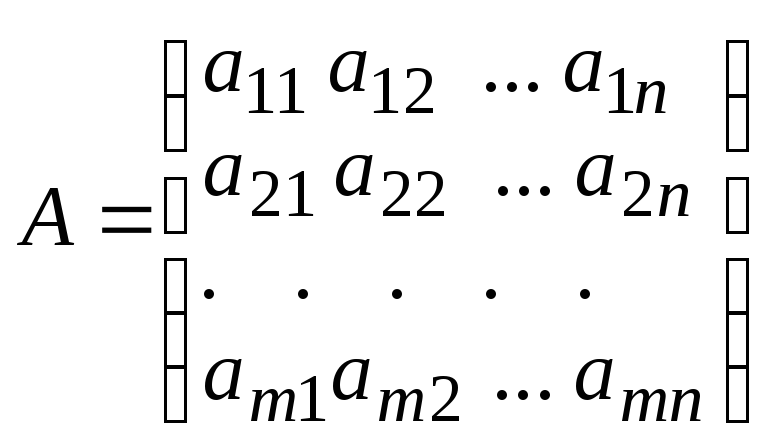произвольно выделено k строк и k столбцов. Элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу порядка k, определитель которой называется м и н о р о м k-г о п о р я д к а матрицы.

Максимальный порядок r отличных от нуля миноров мат-рицы называется р а н г о м м а т р и ц ы и обозначается r (А). Любой минор порядка r, отличный от нуля, называется б а з и с- н ы м м и н о р о м.

Основные м е т о д ы в ы ч и с л е н и я р а н г а м а т р и- ц ы.

Метод окаймляющих миноров. Пусть в матрице найден минор k-го порядка М_k, отличный от нуля. Рассмотрим лишь те миноры (k+1)-го порядка, которые содержат в себе (окаймляют) минор М_k; если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой минор (k+1)-го порядка, и вся процедура повторяется.

Метод элементарных преобразований. Следующие преобразования матрицы называются э л е м е н т а р н ы м и :

1. перестановка строк (столбцов); 2) умножение строки (столбца) на отличное от нуля число; 3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (другого столбца), предварительно умноженных на некоторое число.

Элементарные преобразования не меняют ранга матрицы. Используя эти преобразования, матрицу можно привести, например, к треугольному виду, затем подсчитать количество r отличных от нуля диагональных элементов, которое будет равно рангу матрицы А, т.е. r (А) = r.

Обратная матрица.

Известно, что если данная квадратная матрица

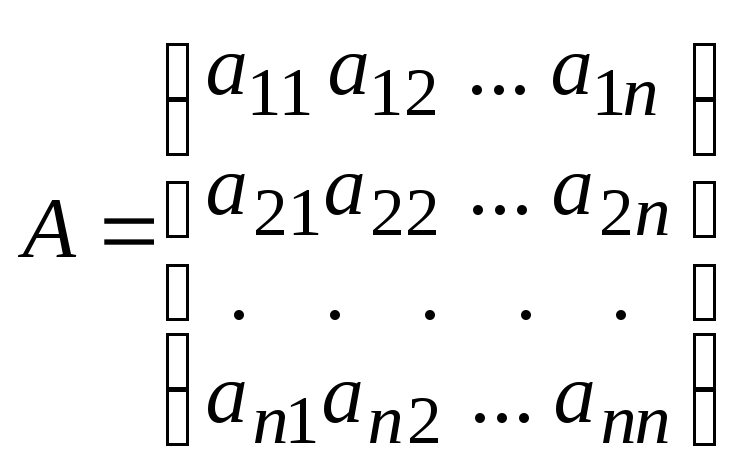
является невырожденной, то существует, и притом единственная, матрица А^-1такая, что выполняется равенство АА^-1 А^-1 АЕ, где Е – единичная матрица. Матрица А^-1 называется о б р а т н о й к матрице А.

Основные м е т о д ы в ы ч и с л е н и я о б р а т н о й м а т р и ц ы .

1) Метод присоединенной матрицы.Если матрица А невырожденная, то обратная для нее матрица А^-1единственна и может быть записана в виде

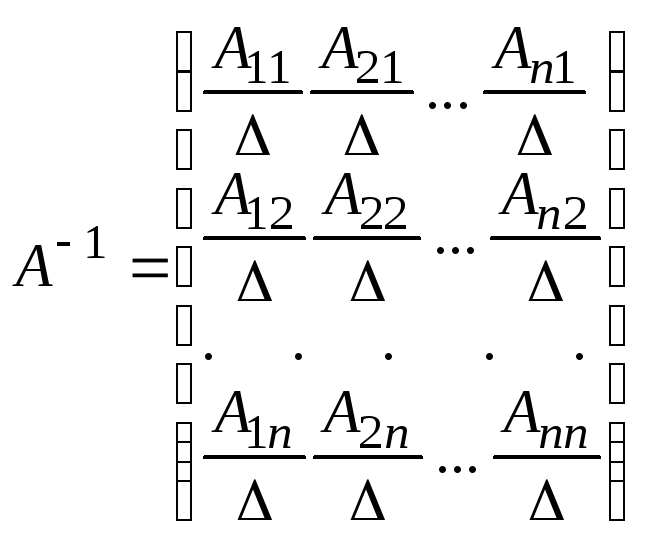, где А_ij– алгебраические дополнения элементов а_ijопределителя, причем алгебраические дополнения строк и столбцов меняются местами. Матрицавида А* =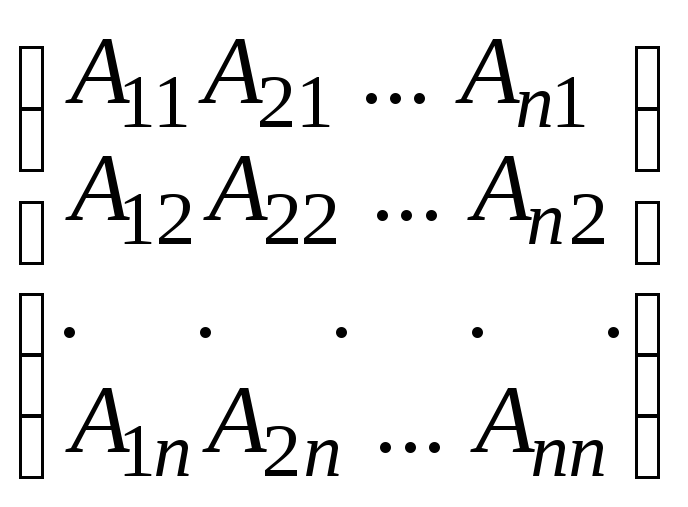называется п р и с о е д и н е н н о й к матрице А. Итак, если А н вырожденная матрица, то.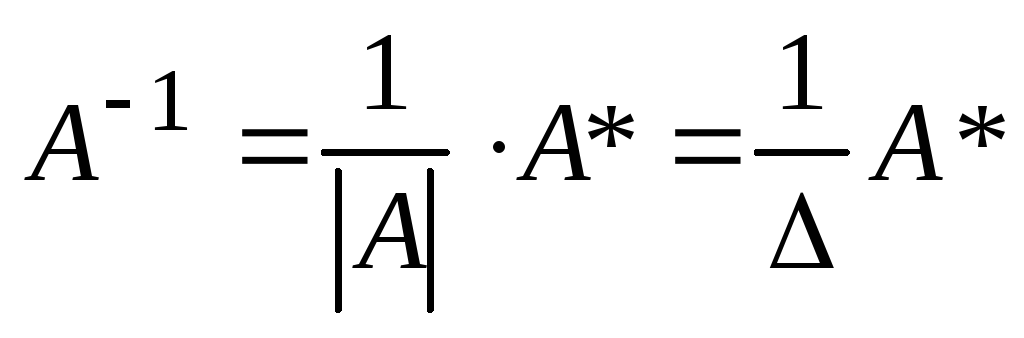

2) Метод элементарных преобразований (вычисление обратной матрицы по схеме Жордана-Гаусса). Для данной матрицы А n-го порядка, приписывая к ней через вертикальную черту справа единичную матрицу Е, записываем прямоугольную (размеровn2n) матрицу. (5)

Выполнив элементарные преобразования над строками, приводим матрицу (5) к виду, тогда С = А^-1.

Осн. лит.: 1, § 1,2,3,4, [5-33] , 6, § 1,3, [12-42]; [66-83], 19, Глава 1.8- 1.12, 1.14, [52-58] , [72-83, 87-94]

Контрольные вопросы

1. Что такое определитель второго порядка, 3-го порядка? Укажите основные свойства определителей.

2. Укажите способы вычисления определителей.

3. Что называется рангом матрицы?

4. Какие методы служат вычислению ранга матрицы.?

5. Перечислите основные методы вычисления обратной матрицы.

Лекция 2. Системы n линейных уравнений с n неизвестными. Правило Крамера. Матричное решение систем линейных уравнений. Необходимое и достаточное условие совместности системы. Метод Жордана-Гаусса. Системы линейных однородных уравнений. Приложение линейной алгебры в экономике.

Пусть задана система n линейных уравнений с n неизвестными:

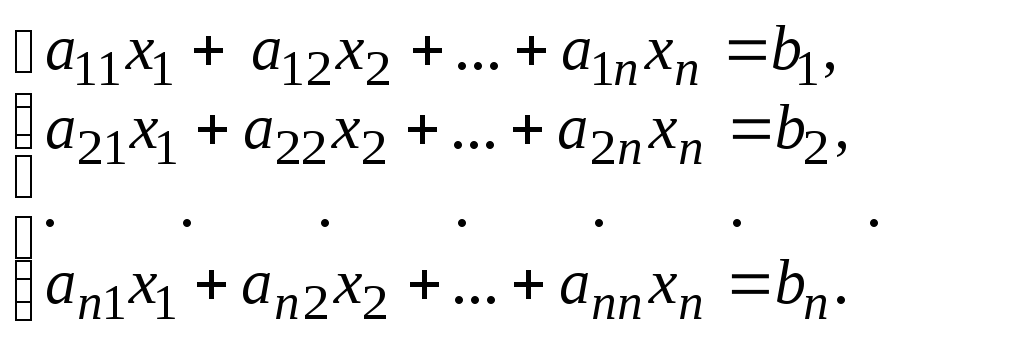(6)

Из коэффициентов при неизвестных составим квадратную матрицу, т.е.

.

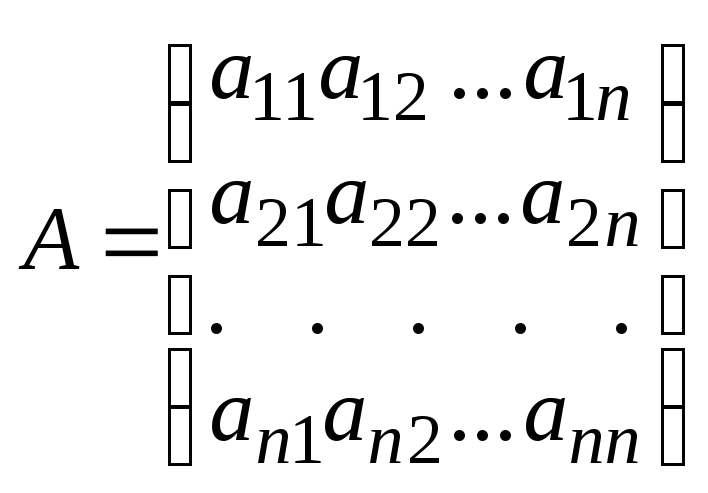Правило Крамера. Если для системы (6) определитель, то эта система имеет, и притом единственное,решение ,

где  _i – определитель, полученный из определителя  заменой i-го столбца на столбец свободных членов.

Если в системе (3) свободные члены b₁=b₂=…=b_n=0, то она называется с и с т е м о й л и н е й н ы х о д н о р о д н ы х у р а в н е н и й и имеет вид

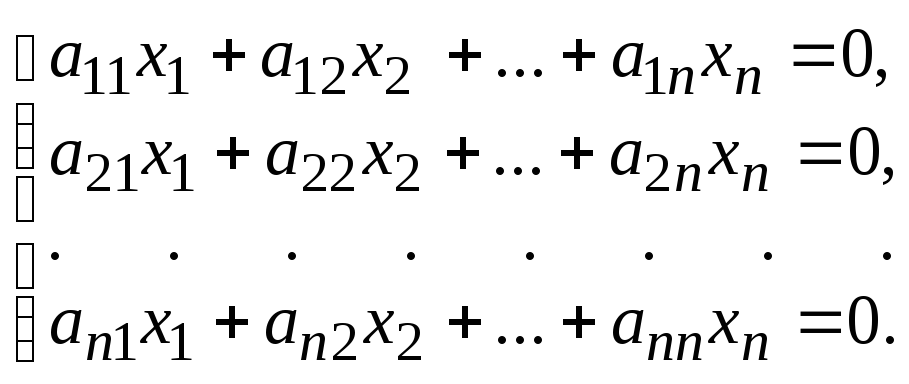
По правилу Крамера система (4) имеет решение, и притом единственное, при условии, что . Это решение х₁ = х₂ = … = х_n= 0 называется т р и в и а л ь н ы м .

Матричный метод решения систем линейных уравнений.

Система линейных уравнений

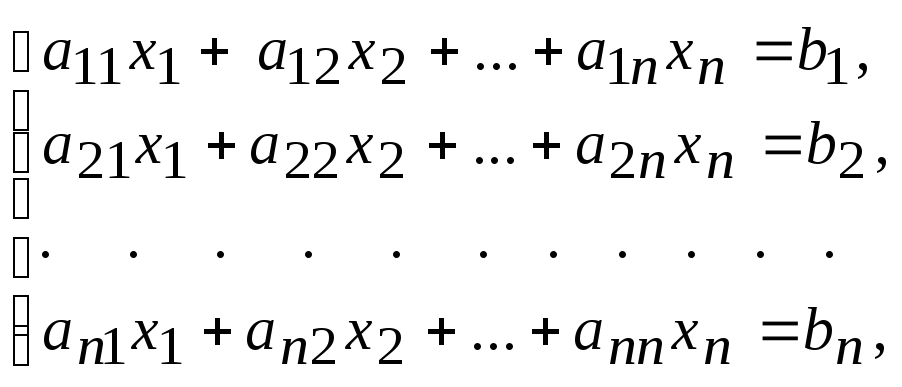(7)

может быть записана в виде эквивалентного ей м а т р и ч н о- г о уравнения

А Х = В, (8)

где

,,.

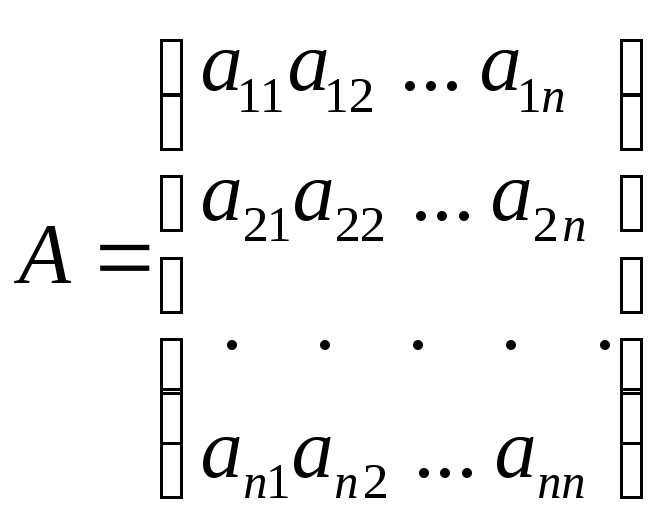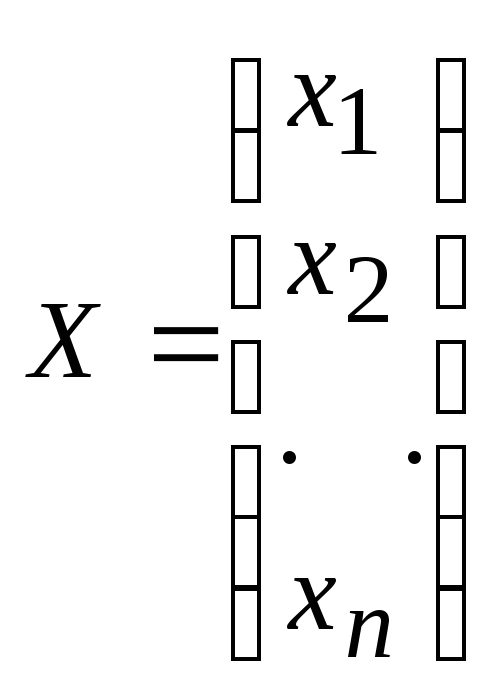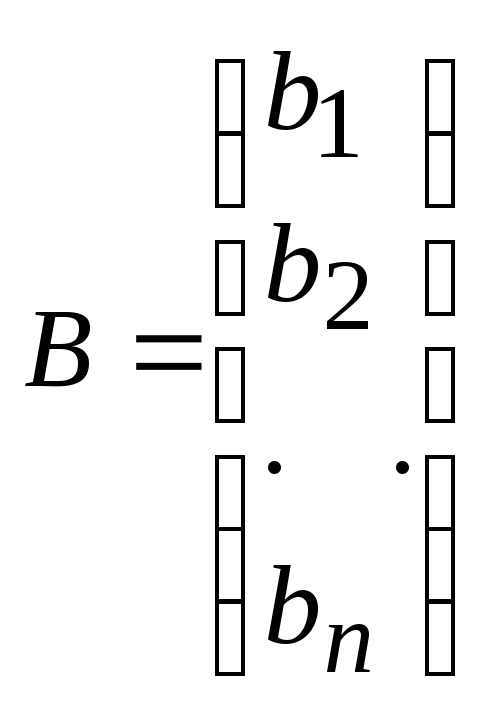Р е ш е н и е матричного уравнения (8), а следовательно, и системы (7) может быть записано, если А – невырожденная, с помощью обратной матрицы в виде

Х = А^-1В. (9)

Необходимое и достаточное условие совместности системы.

Система т линейных уравнений с п неизвестными

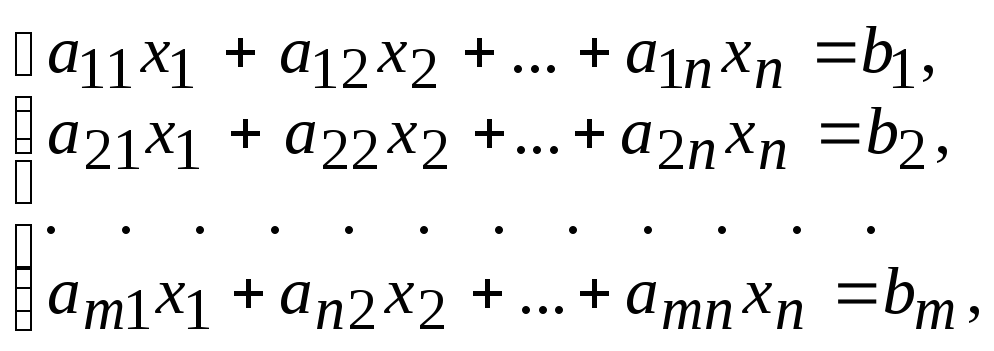(10)

где в общем случае т  п, называется п р о и з в о л ь н о й, в отличие от квадратной, для которой т  п. Обозначим через

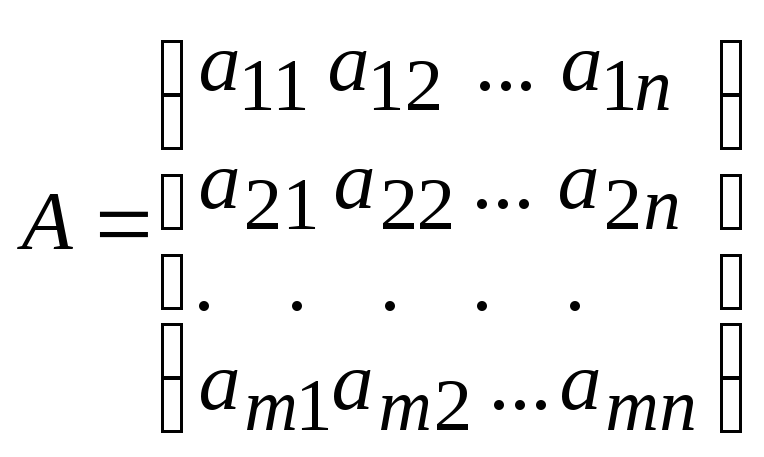
матрицу из коэффициентов при неизвестных системы (10), через В и Х:

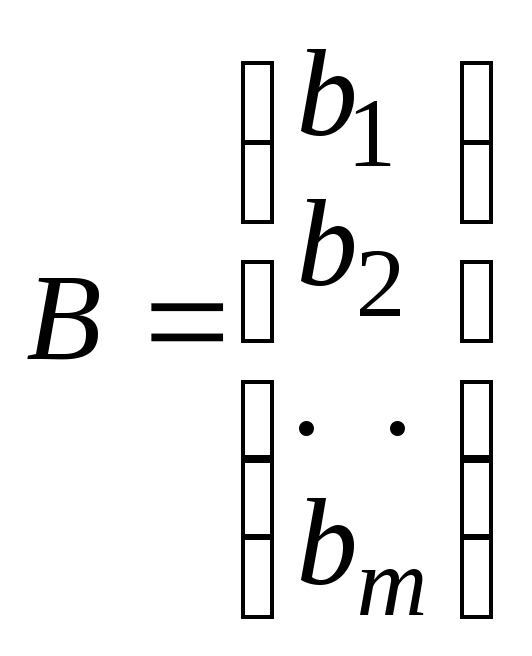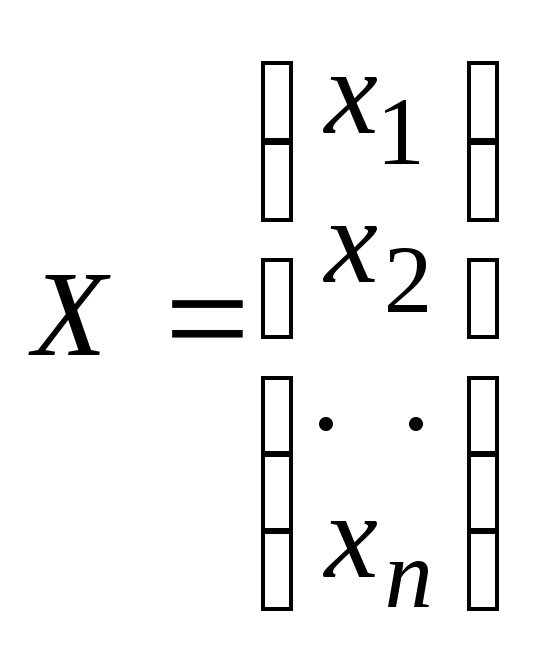, – столбец ее свободных членов и столбец из неизвестных соот-ветственно. Тогда систему (11) можно записать в виде м а т -р и ч н о г о у р а в н е н и я:

. (11)

Р е ш е н и е м с и с т е м ы (11) называется всякий п-мер-ный вектор-столбец Х, обращающий матричное уравнение (11) в верное равенство.

Система называется с о в м е с т н о й, если она имеет по крайней мере одно решение, и н е с о в м е с т н о й в противном случае.Две системы называются э к в и в а л е н т н ы м и, если множества их решений совпадают.

Э л е м е н т а р н ы м и преобразованиями системы назы-ваются следующие преобразования: 1) перестановка уравнений; 2) умножение обеих частей одного из уравнений на любое, отличное от нуля, число; 3) прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на некоторое число; 4) вычеркивание строки, состоящей из одних нулей.

Элементарные преобразования переводят данную систему уравнений в эквивалентную систему.

Теорема Кронекера-Капелли (критерий совместности системы). Для того, чтобы система (10) была совместной, необ-ходимо и достаточно, чтобы (12),

где 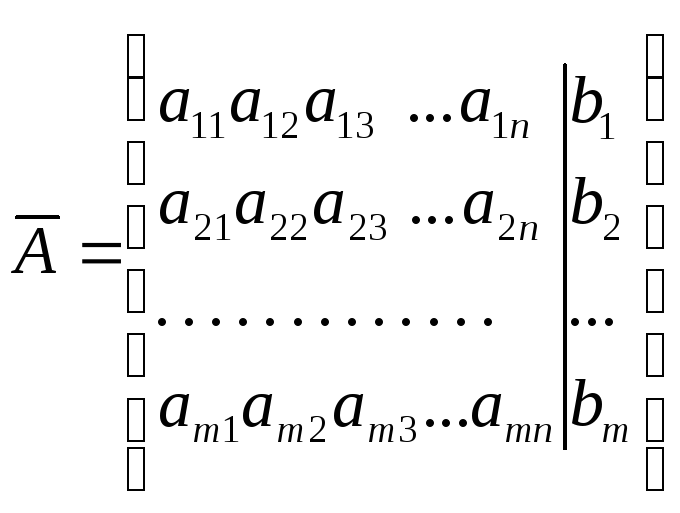– расширенная матрица системы.

Метод Жордана-Гаусса.

Сущность метода Жордана-Гаусса заключается в приведении системы (10) с помощью элементарных преобразований к виду:

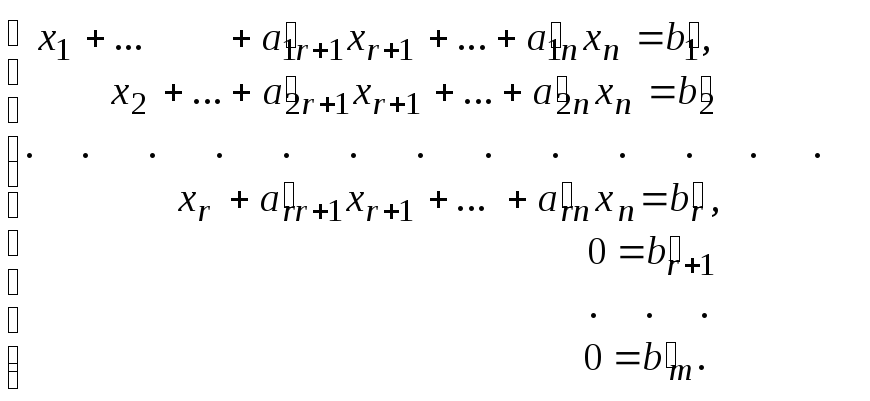(13)

Если хотя бы одно из чисел отлично от нуля, то система (14), а следовательно, исходная система (10) несовместны.Если же , то система совместна и при: а)имеет единственное решение:; б)r  n – имеет бесконечное множество решений, каждое из которых отыскивается так. Придавая переменным х_r+1, … , х_n произвольные числовые значения с_r+1,… , с_n находим соответствующие значения переменных х₁, х₂, … , х_r по формулам

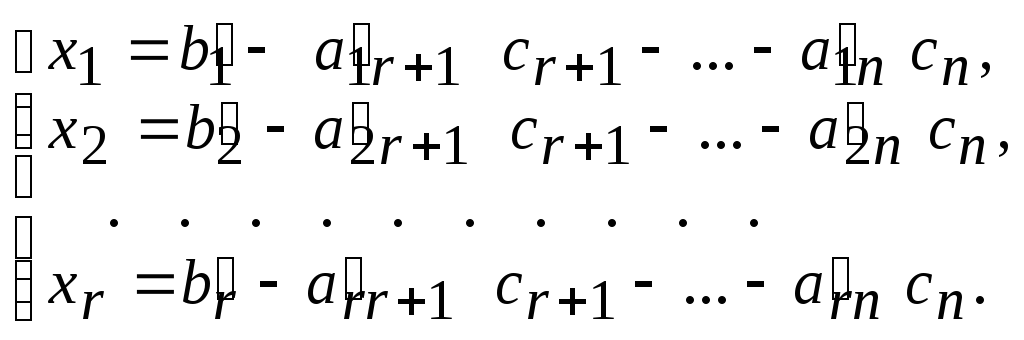(14)

Множество всех решений можно записать в виде

,

где х₁, х₂, …, х_r вычисляются по формулам (14).

Переменные х₁, х₂, …, х_r называются б а з и с н ы м и неизвестными, а х_r+1=c_r+1, х_r+2=c_r+2, … х_n=c_n – с в о б о д н ы м и неизвестными. Придав свободным неизвестным нулевые значения, получим решение системы (₁, ₂, …, _r , 0, 0, … , 0), которое называется б а з и с н ы м р е ш е н и е м .

Совместную систему уравнений называют о п р е д е- л е н н о й , если она имеет единственное решение и – н е о п- р е д е л е н н о й , если она имеет более одного решения.

Определение. Системаmлинейных уравнений сnпеременными называется системой линейных однородных уравнений, если все их свободные члены равны нулю. Такая система имеет вид:

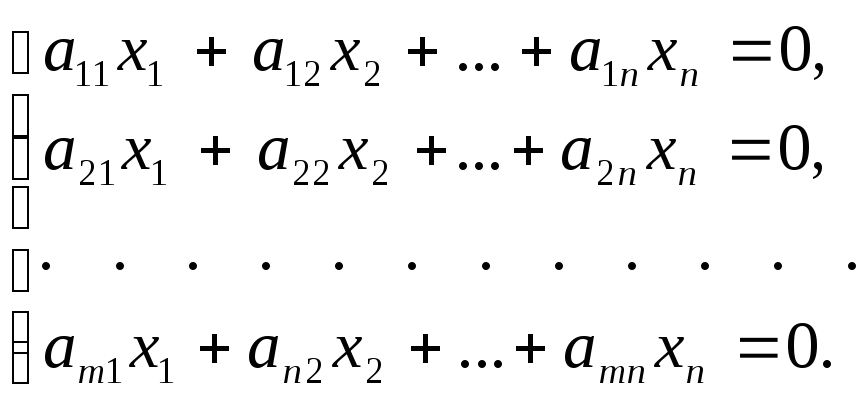(15)

Система линейных однородных уравнений всегда совместна,т.к. она всегда имеет нулевое тривиальное решение. Если m=n, и ее определитель не равен нулю, то такая система уравнений имеет только нулевое решение (очевидность следует из формул Крамера). Следовательно, ненулевые решения возможны в двух случаях: 1)m=n и Δ =0; 2)m<n. Т.о. система линейных однородных уравнений имеет ненулевые решения тогда и только тогда, когда ранг ее матрицы коэффициентов при переменных меньше числа переменных; т.е. при приr(A) <n.

Обозначим решение системы линейных однородных уравнений : x₁=k₁,x₂=k₂, …,x_n=k_n в виде строкиe₁=(k₁,k₂,…,k_n) . Решения системы линейных однородных уравнений обладают следующими свойствами: 1) Если строкаe₁=(k₁,k₂,…,k_n) – решение этой системы, то и строка λe₁=(λk₁,λk₂,…,λk_n) – также решеение этой системы.; 2) Если строкиe₁=(k₁,k₂,…,k_n) и e₂=(l₁,l₂,…,l_n)- решения системы, то при любых с₁и с₂их линейная комбинация с₁e₁+c₂e₂=(c₁k₁+с₂l₁,c₁k₂+с₂l₂, …c₁k_n+с₂l_n) – также решение данной системы. Доказательство этих свойств следует непосредственно из подстановки решений в систему уравнений. Отсюда, всякая линейная комбинация решений системы линейных однородных уравнений также является решением данной системы.

Определение:Система линейных независимых решений е₁,е_2,…е_kназывается фундаментальной, если каждое решение системы является линейной комбинацией решений е₁,е_2,…е_k.

Справедлива следующая теорема:Если рангrматрицы коэффициентов при переменных системы линейных однородных уравнений меньше числа переменныхn, то всякая фундаментальная система решений данной системы уравнений состоит изn-rрешений. Поэтому, общее решение системы (15) имеет вид:c₁e₁+c₂e₂+…+c_ke_k гдеe_1,e₂,…e_k– любая фундаментальная система решений,c₁ , c₂,…c_{k -} -произвольные числа иk=n–r.

Известно, что общее решение системы mлинейных уравнений (10) равно сумме общего решения соответствующей ей системы однородных уравнений (15) и произвольного частного решения системы (10).

Приложение линейной алгебры в экономике

Элементы линейной алгебры часто используются в экономических задачах.

Пример:Предприятие производитnтипов продукции, объемы выпуска заданы матрицей А размерами 1×n. Цена реализации единицыi– го типа продукции вj-м регионе задана матрицей В размерамиn×k, гдеk– число регионов, в которых реализуется продукция. Найти С - матрицу выручки по регионам. Пусть А=(100,200,100); В =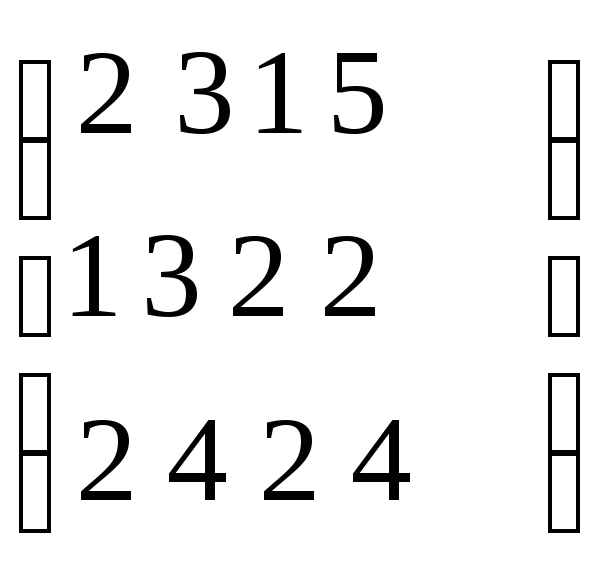

Решение: Выручка определяется матрицей С = АВ, причем с_1j- это выручка предприятия вj–м регионе.

С=(100,200,100) 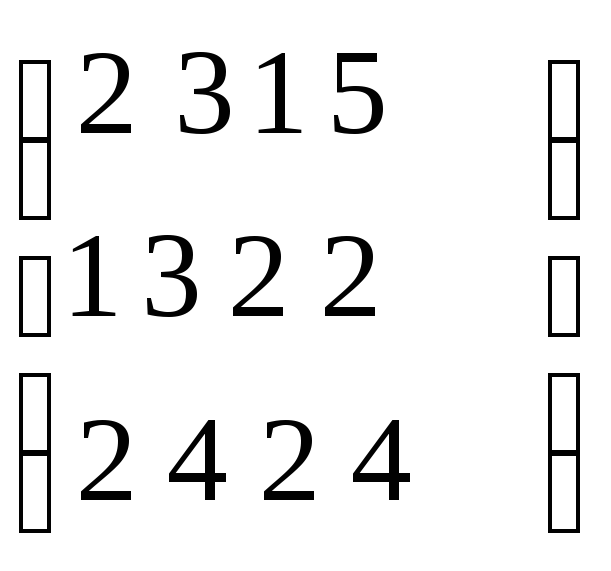=(600,1300,700,1300).

В качестве следующего примера рассмотрим модель Леонтьевамногоотраслевой экономики (межотраслевой баланс в стоимостном выражении).

Пусть рассматривается экономическая система, состоящая из nвзаимосвязанных отраслей производства. Обозначим через х_iстоимость продукции, произведенной вi-ой отрасли (например, в течение года). Продукция этой отрасли частично используется в других отраслях или же в данной отрасли на производственные нужды, а оставшаяся часть ее образует конечный продукт, который обозначим через у_i. Обозначим черезx_ijстоимость продукцииi-ой отрасли, потребляемой вj-ой отрасли. Распределение продукции тогда можно представить следующей таблицей межотраслевых связей. Величины, расположенные в строках этой таблицы, связаны следующими б а л а н с о в ы м и уравнениями

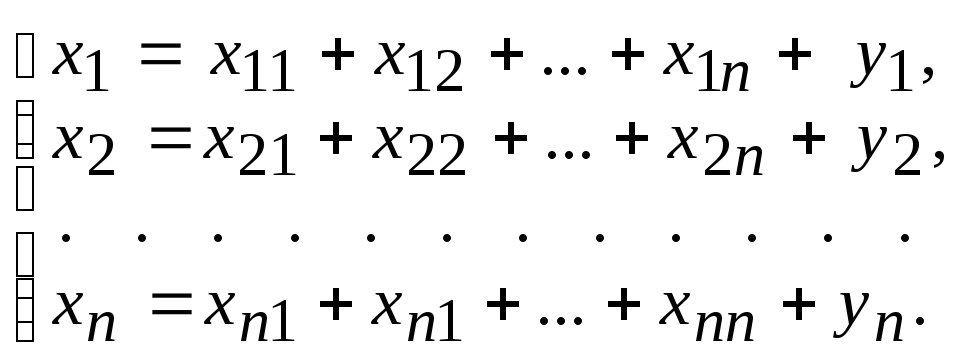(1)

Обозначим через a_ijстоимость продукцииi-ой отрасли, потребляемой на производство стоимостной единицы продукцииj-ой отрасли, тогда

. (2)

Величины a_ijназываются коэффиц и е н т а м и п р я м ы х з а т р а т (или т е х н о л о г и ч е с к и м и к о э ф ф и ц и е н т а м и ); они образуют следующую матрицу:

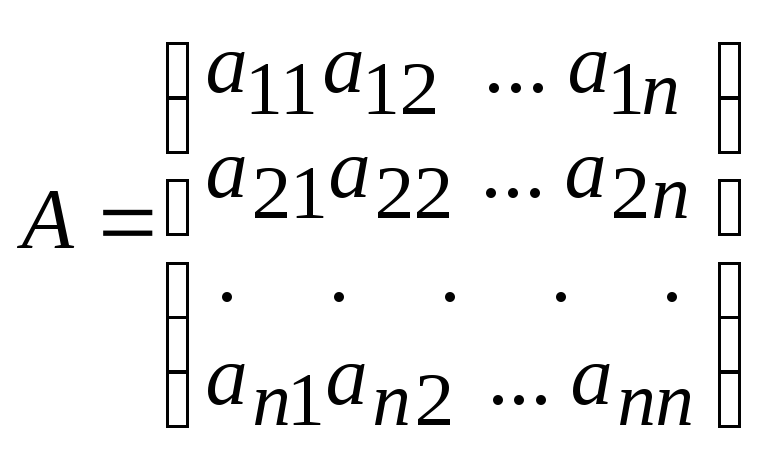, (3)

которая называется м а т р и ц е й п р я м ы х з а т р а т (или т е х н о л о г и ч е с к о й м а т р и ц е й ).

Отрасль	Стоимость продукции	Межотраслевые потоки				Итого на производственные нужды	Конечный продукт
		1	2	. . .	n
1 х1х11х12. . .x1n y1 2 x2x21x22. . .x2n y2 . . . . . . . . . . . . . . . . . . . . . . . . nxnxn1xn2 . . .xn2 yn

Совокупность значений у₁, у₂, … , у_n, характеризующих выпуск конечного продукта, называют в е к т о р о мYкон е ч н ы х п р о д у к т о в ; а совокупность значений х₁, х₂, … , х_n, определяющих валовый выпуск всех отраслей, – в е к т о р - п л а н о м Х. Записывают каждую из совокупностей в виде матрицы-строки или в виде матрицы-столбца. Например,

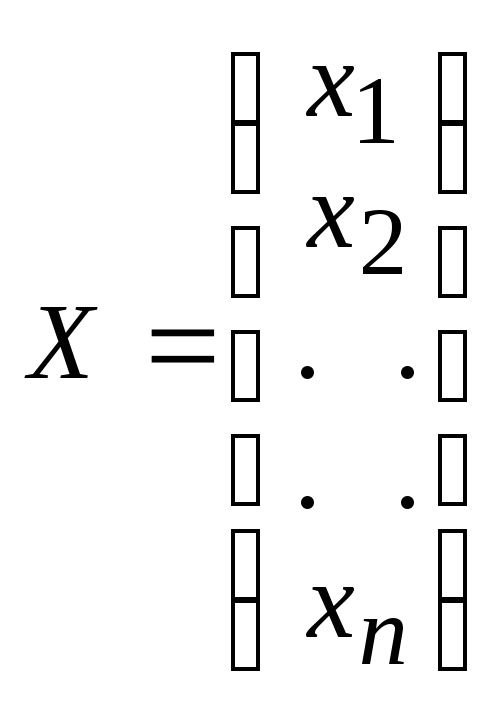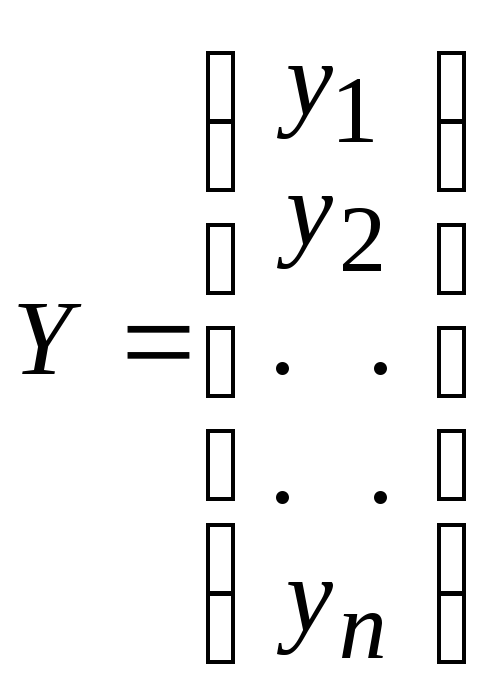,. (4)

Используя из формул (2) значения , систему (1) балансовых уравнений можно переписать в виде

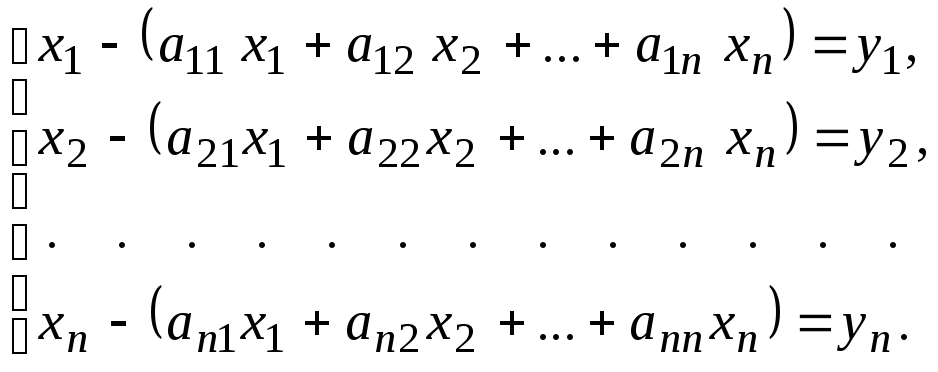(5)

Вследствие обозначений (3) и (4) система (5) равносильна матричному уравнению

Х – АХ = Yили (Е - А)Х =Y (6)

Единственное решение этого уравнения запишется формулой

Х = ( Е – А ) ^-1Y. (7)

Итак, если задан вектор Yконечных продуктов и найдена матрица В = ( Е – А )^–1, то по формуле (7) можно определить вектор-план Х = ( х₁, х₂, … , х_п ).

Очевидно, при данной матрице А = ( a_ij) прямых затрат каждому варианту вектораYконечных продуктов соответствует определенный вариант вектор-плана Х.

Собственные векторы и собственные значения матрицы

Число λ называется собственным значением (или характеристическим числом) квадратной матрицы А порядка n, если можно подобрать такой n-мерный ненулевой вектор x, что Аx = λx.

Множество всех собственных значений матрицы А совпадает с множеством всех решений уравнения | А – λЕ | = 0, где λ – независимая переменная. Если раскрыть определитель | А – λЕ | , то получится многочлен n-й степени относительно λ:

| А – λЕ | =

Этот многочлен называется характеристическим многочленом матрицы А. Отметим, что Уравнение | А – λЕ | = 0 называется характеристическим уравнением матрицы А.

Ненулевой вектор x называется собственным вектором квадратной матрицы А, принадлежащим ее собственному значению λ, если Аx = λx.

Пример 2.9 Найти собственные значения и собственные векторы матрицы . Запишем характеристическое уравнение матрицы:

| А – λЕ | =

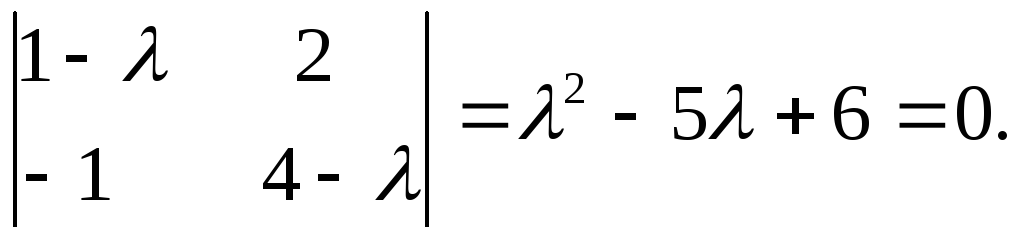
Его корни являются собственными значениями матрицы А. Найдем собственные векторы, принадлежащие собственным значениям. Собственный вектор, принадлежащий собственному значению, является ненулевым решением системы

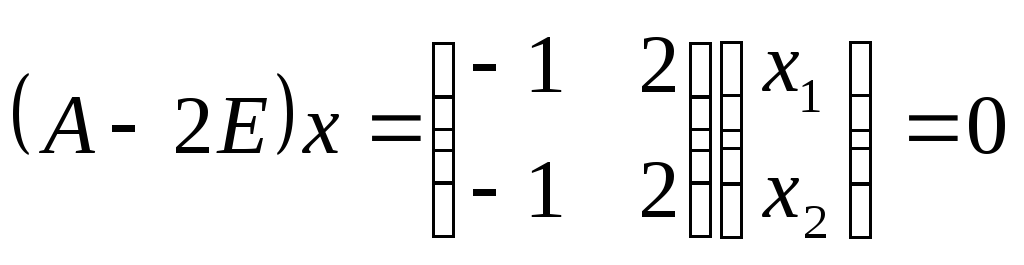или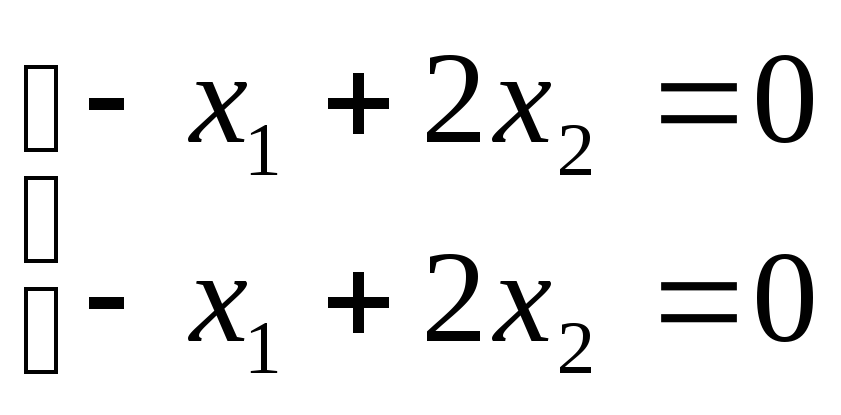

Тогда – ненулевое решение и, значит,– искомый собственный вектор.

Осн. лит.: 1, § 1,2,3,4, [5-33] , 6, § 1,3, [66-83], 12, 14.

Контрольные вопросы

1. Матричный способ решения систем линейных уравнений. Когда он применяется?

2. Какие системы линейных уравнений называются совместными?

3. Опишите метод Жордана-Гаусса решения систем линейных уравнений.

4. Что называется рангом системы линейных уравнений?

5. Сколько решений имеет система линейных уравнения, если: а)r=n; б) r<n.

6. В чем состоит основная задача межотраслевого баланса?

Лекция 3. Векторная алгебра.

Векторы и линейные операции над ними. Скалярное и векторное произведения.

Смешанное произведение трех векторов.Плоскость. Уравнения прямой на плоскости. Прямая в пространстве. Угол между прямыми. Прямая и плоскость.

Векторы используются для описания величинимеющих определённое направление. Примерами таких величин являются сила, скорость, перемещение.

Определение.Вектором называется отрезок с выбранным направлением, или направленный отрезок.

Вектор с началом в точке A и с концом в точке B обозначается через , кроме тоговектор можно обозначать одним символом, например. Вектор, у которого начало совпадает с его концомназывается нулевым вектором и обозначается через. Длина отрезка, изображающего вектор , называется модулем этого вектора и обозначается ||.

Векторы , параллельные одной прямой называются коллинеарными. Нулевой вектор считается коллинеарным любому вектору.

Два вектора и считаются равными, если они равны по модулю, коллинеарны и одинаково направлены. Из этого определения следует, что при параллельном переносе вектор не меняется, по этому в качестве начала вектора можно выбрать любую точку.

Линейными операциями над векторами называются умножение вектора на число и сложение векторов.

Линейные операции над векторами обладают следующими свойствами.

1= 0=



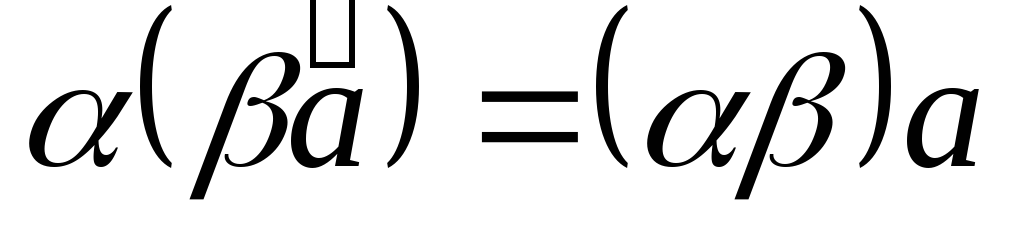
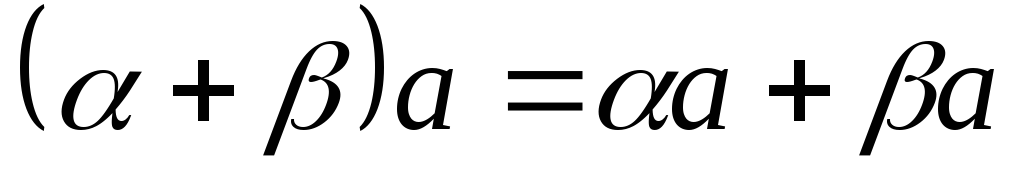
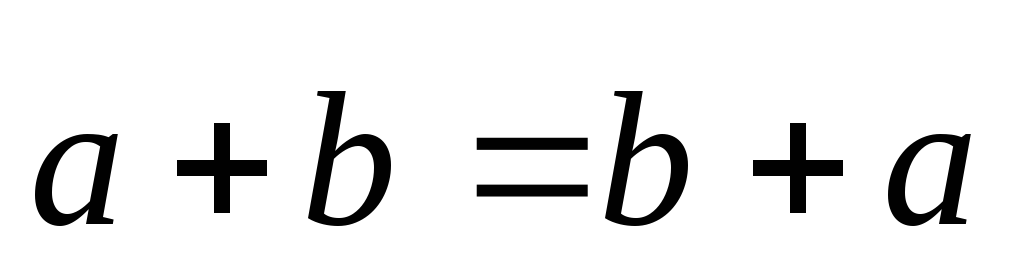
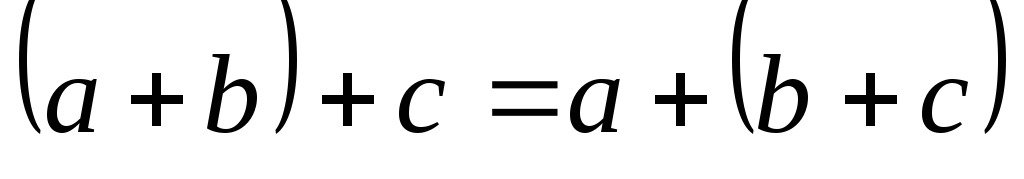
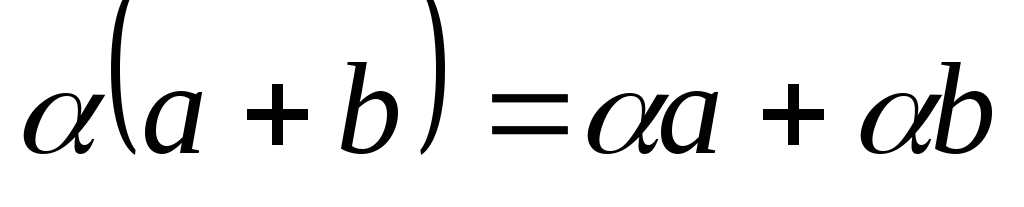
Определение.Любой ненулевой векторна прямой называется базисным вектором этой прямой. Любая пара неколлинеарных векторовплоскости называется базисом этой плоскости. Любая тройка некомпланарных векторовназывается базисом пространства.

Теорема.Пусть в декартовой системе координатOxyzзаданы две точкиA(x_A,y_A,z_A) иB(x_B,y_B,z_B), тогда в базисе {,,} вектор имеет координаты ((x_В–x_А),(y_В–y_А),(z_В–z_А)).

Скалярное произведение векторов и его свойства

Имеются три вида произведений векторов: скалярное, векторное и смешанное. Название первого из них произошло от слова скаляр – число. Скалярная величина в математике – это величина, принимающая численные значения.

Определение.Скалярным произведением векторовиназывается число, равное произведению модулей этих векторов на косинус угла между ними, т. е. . Скалярное произведение обозначается символами.

Свойства скалярного произведения

1⁰. Для любых векторови:, т.е. это произведение коммутативно.

2⁰. Для любого вектора:.

3⁰. Скалярные произведение ненулевых векторовиравнотолько в том случае, когда эти векторы ортогональны (перпендикулярны).

4⁰. Для любых векторовиверно соотношение .

5⁰. Для любого векторас координатамив базисеверно

,,.

6⁰. Постоянный множитель можно выносить за знак скалярного произведения, т.е. для любых векторов,и числаверно:.

7⁰. Cкалярное произведение обладает свойством дистрибутивности, т.е. для любых векторов:.

Векторное произведение векторов и его свойства

Это произведение определено только для пространственных векторов и, и оно обозначается символамиили

Определение.Векторным произведением векторовиназывается вектор, удовлетворяющий трём условиям: а) Модуль вектораравен произведению модулей векторовина синус угла между ними:sin; в)перпендикулярен векторамит.е. он перпендикулярен плоскости, проходящей через вектораи; с) Тройка векторовправая.

Cмешанное произведение векторов и его свойства

Определение. Смешанным произведением трех векторов называется число, равное скалярному произведению векторного произведения векторовс вектором.

Оно обозначается символами или:.

Свойства смешанного произведения.

1⁰ Смешанное произведение векторов равнообъему параллелепипеда, построенного на этих векторах:

Здесь знак “+” берется в случае если тройка векторов  правая “” если она левая.

2⁰ Векторы  являются компланарными только в том случае когда их смешанное произведение равно 0:

3⁰ При перестановке местами любых двух векторов смешанного произведения оно меняет свой знак на противоположный; т.е.

4. Постоянный сомножитель можно выносить из любого сомножителя смешанного произведения т.е. для любых векторов и числа.

5. Смешанное произведение дистрибутивно для любого сомножителя т.е. для любых векторов верно:.

Теорема. Пусть в базисе векторыимеют координаты соответственно и, тогда их смешанное произведение записывается в виде определителя: .

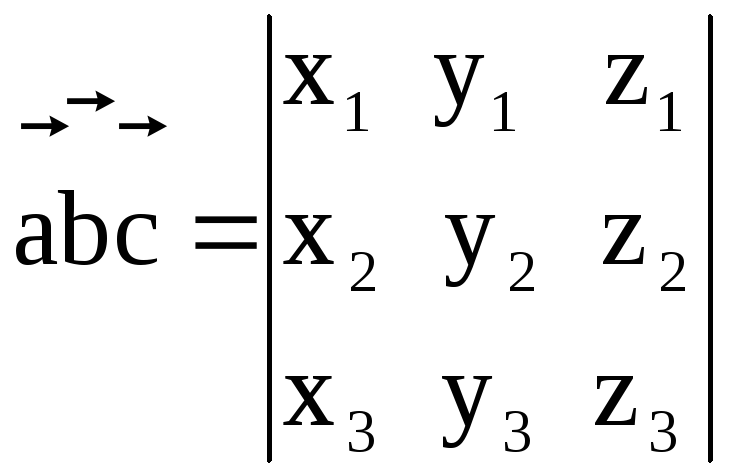Аналитическая геометрия.Плоскость

Пусть плоскость проходит через три точки,и, не лежащие на одной прямой. Тогда векторыиявляются направляющими для плоскости, подставив их координаты в уравнение с направляющими векторами, получим:.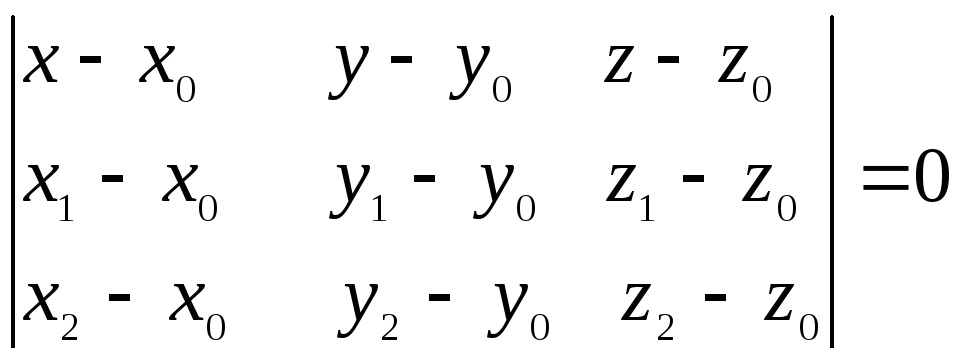

Это уравнение называется уравнением плоскости, проходящей через три заданные точки.

Теорема.Любая плоскостьв пространствеопределяется своим общим уравнением вида, где, задает некоторую плоскость в пространстве.

Определение.Вектор, перпендикулярный плоскости, называется нормальным вектором этой плоскости.

Теорема о нормальном векторе плоскости.Векторс координатамиявляется нормальным для плоскостис уравнениемв пространстве.

Следствие 1.Косинус угламежду плоскостями

и

с нормальными векторами инаходится по формуле:

.

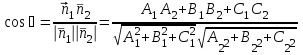Следствие 2.Эти плоскости перпендикулярны только в том случае, когда

.

Следствие 3.Эти плоскости параллельны только в том случае, когда.

Если , то плоскостиисовпадают.

Пусть плоскость проходит через точкуперпендикулярно вектору. Возьмем на плоскости произвольную точкуM(x,y,z) и составим вектор=. При любом расположении точки М на плоскости вектораивзаимно перпендикулярны, поэтому их скалярное произведение равно нулю.=0. Тогда. Это уравнение называется уравнениемплоскости с нормальным вектором.Пусть плоскостьне проходит через начало координат и пересекает осив точках с координатамиисоответственно. Тогда уравнение этой плоскости имеет вид:. Это уравнениеплоскости в отрезках.

Теорема.Расстояние от точкидо плоскостиопределяется формулой:.

Прямая в пространстве

Пусть в пространстве имеется прямаяс направляющим вектором(рис. 1).– фиксированная точка этой прямой,– произвольная точка на. 1. Запись векторного уравнения прямой

2. Записав три координаты обеих частей векторного уравнения прямой, получим

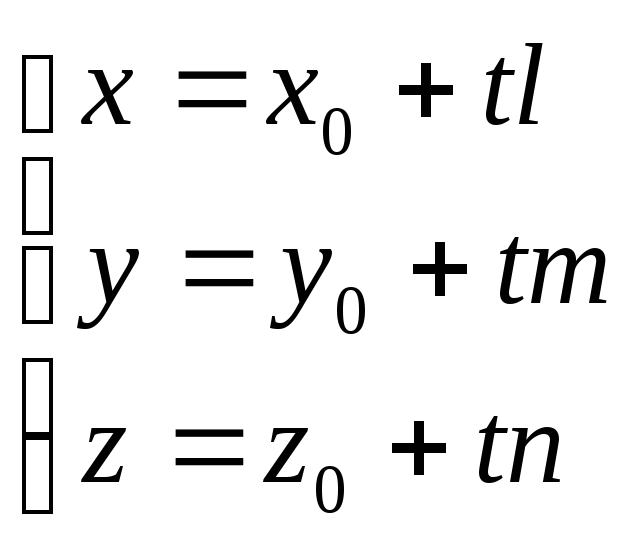
Эти уравнения называются параметрическими уравнениями прямой в пространстве.

3. Поскольку векторы иколлинеарны, то их координаты пропорциональны, поэтому.

Эти уравнения называются каноническими уравнениями прямой в пространстве. В соответствии с количеством знаков равенства таких уравнений два и понимать их нужно в смысле пропорций.

Из-за того, что в знаменателях канонических уравнений могут оказаться нули, предпочтительнее пользоваться параметрическими уравнениями.

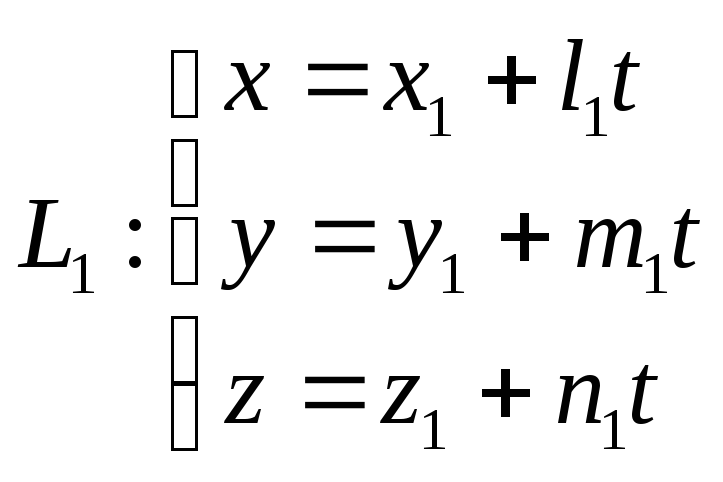Теорема 1.Косинус угламежду прямымии

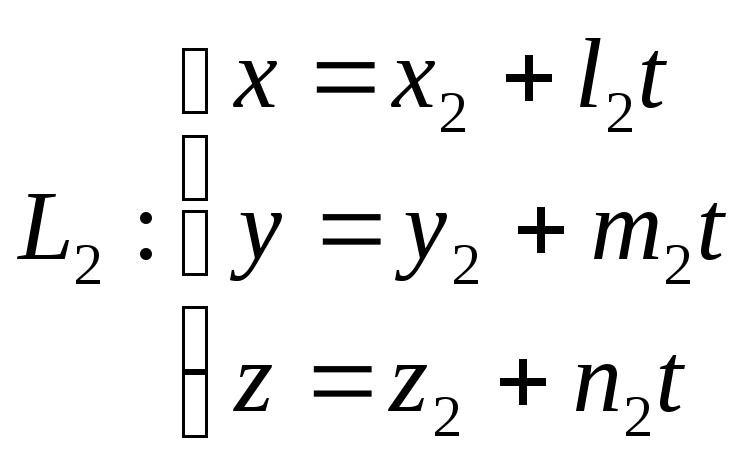
находится по формуле .

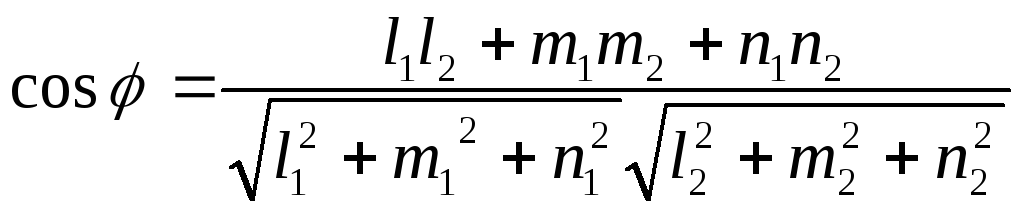Эти прямые перпендикулярны только в том случае, когда .

Эти прямые параллельны только в том случае, когда .

Если при выполнении этого условия , то прямыеисовпадают. Все утверждения этой теоремы следуют из соответствующих свойств направляющих векторов. В последнем случае прямыеиимеют общую точку.

Теорема 2.Синус угла между плоскостьюи прямой

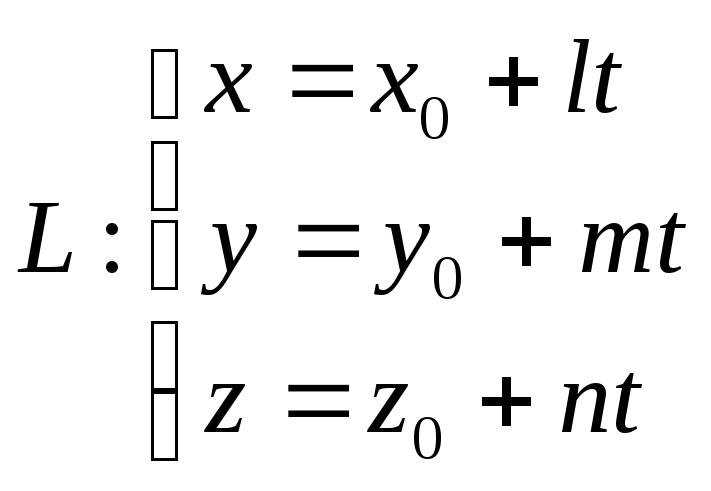находится по формуле:

.

Прямая и плоскость перпендикулярны только в том случае, когда .

Прямая параллельна плоскости только в том случае, когда .

Если при выполнении этого условия , то прямаялежит в плоскости.

4. Две параллельные плоскости в пересечении определяют прямую в пространстве. Система из двух уравнений этих плоскостей с тремя неизвестными называется общими уравнениями прямой: .

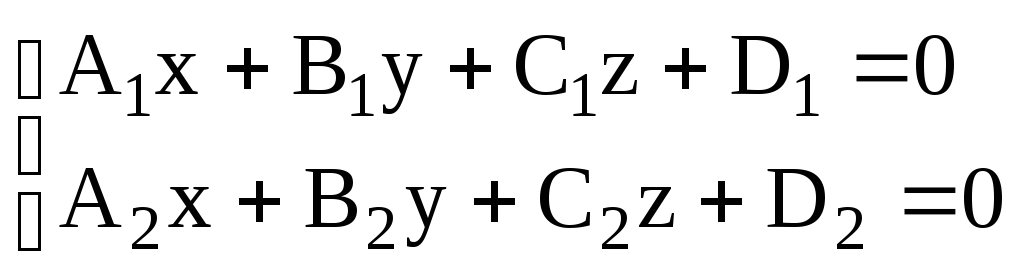5. Пусть – проекция точкина,и– произвольная точка на этой прямой (рис. 2).Y

N





X

OLРис. 2

Тогда .

Окончательно получаем, что . Это уравнение называется нормальным уравнением прямой. Обратим внимание, что здесь свободный член –уравнения всегда отрицателен, а, т.к.– единичный вектор. Поэтому, чтобы из общего уравнения прямойполучить ее нормальное уравнение, необходимо умножить его на число, где знакберется противоположным знаку С.

30