
- •Министерство образования и науки
- •Семестровая работа 1
- •Глава I. Механика § 1. Кинематика
- •§ 2. Динамика материальной точки и твердого тела
- •§ 3. Законы сохранения
- •§ 4. Элементы специальной теории относительности
- •§ 5. Элементы механики сплошных сpeд
- •§ 6. Гармонические колебания
- •§ 7. Волновые процессы
- •Глава II. Молекулярная физика и термодинамика § 8. Статистическая физика и термодинамика
- •§ 9. Молекулярно- кинетическая теория
- •§ 10. Статистические распределения
- •§ 11. Основы термодинамики
- •§ 12. Явления переноса
- •§ 13. Реальные газы
- •Семестровая работа 2
- •Глава III. Электричество и магнетизм § 14. Электростатика
- •§ 15. Свойства электростатических полей
- •§ 16. Проводники в электрическоМ поле
- •§ 17. Энергия взаимодействия электрических зарядов
- •§ 18. Постоянный электрический ток
- •§ 19. Магнитное поле
- •§ 20. Явление электромагнитной индукции
- •§ 21. Электромагнитные колебания
- •Cеместровая работа 3
- •Глава IV. Оптика § 22. Понятие о геометрической оптике
- •§ 23. Свойства световых волн
- •§ 24. Дифракция волн
- •§ 25. Электромагнитные волны в веществе
- •Глава V. Квантовая физика § 26. Тепловое излучение
- •§ 27. Экспериментальное обоснование основных идей квантовой теории
- •§ 28. Корпускулярно—волновой дуализм
- •§ 29. Уравнение Шредингера.
- •§ 30. Конденсированное состояние
- •§ 31. Атом и Молекула водорода в квантовой теории
- •Глава VI. Физика атомного ядра § 32. Атомное ядро
- •Некоторые астрономические величины
- •Рекомендуемая литература
- •Содержание
§ 31. Атом и Молекула водорода в квантовой теории
Уравнение Шредингера для атома водорода. Водородоподобные атомы. Энергетические уровни. Ширина уровней в сложных атомах. Принцип Паули. Молекула водорода. Ионная и ковалентная связи. Электронные термы двухатомной молекулы.
Основные формулы
Потенциальная энергия
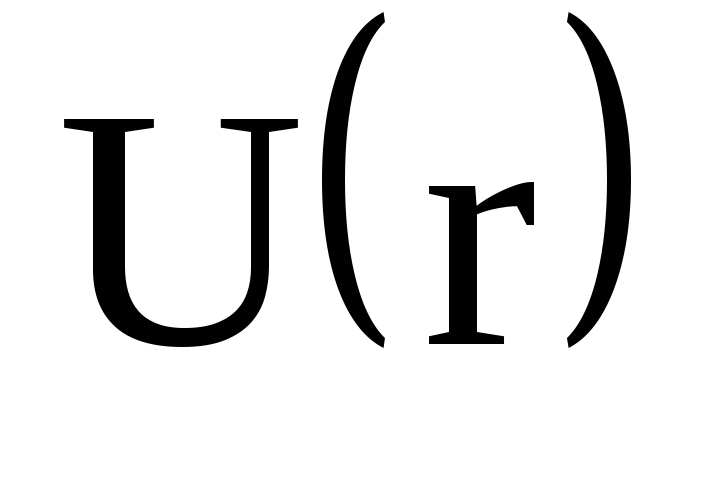 взаимодействия электрона с ядром в
взаимодействия электрона с ядром в
водородоподобном атоме:
![]()
где
![]() расстояние
между электроном и ядром;
расстояние
между электроном и ядром;![]() порядковый
номер элемента;
порядковый
номер элемента;![]() электрическая
постоянная.
электрическая
постоянная.
Собственное значение энергии
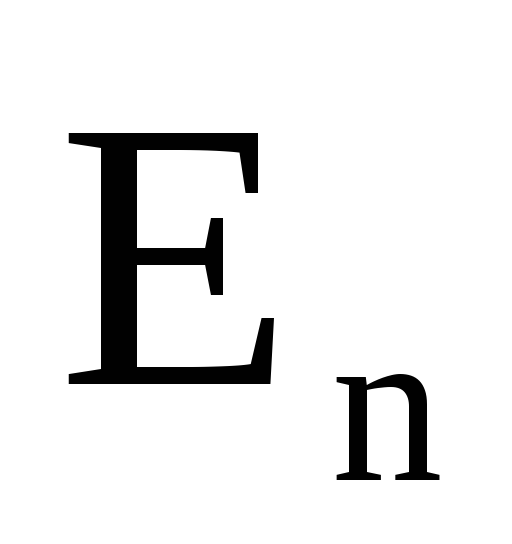 электрона в водородоподобном атоме
электрона в водородоподобном атоме
![]()
![]()
Энергия ионизации атома водорода
![]()
Момент импульса (механический орбитальный момент) электрона
![]() ,
,
где
![]() орбитальное
квантовое число, принимающее при заданном
орбитальное
квантовое число, принимающее при заданном![]() следующие значения:
следующие значения:![]() (всего
(всего![]() значений).
значений).
Проекция момента импульса на направление
 внешнего магнитного поля
внешнего магнитного поля
![]()
где
![]() магнитное
квантовое число, принимающее при заданном
магнитное
квантовое число, принимающее при заданном![]() следующие значения:
следующие значения:![]() (всего
(всего![]() значений).
значений).
Правила отбора для орбитального и магнитного квантовых чисел
![]() 1
и
1
и
![]()
Нормированная волновая функция, отвечающая
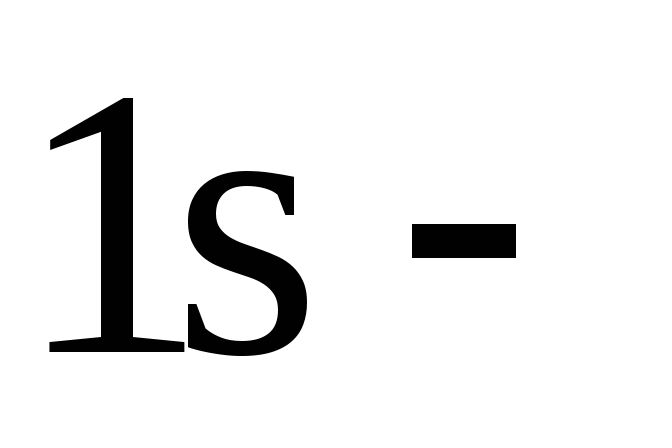 состоянию
состоянию
(основному состоянию n=1, l=0,m=0) электрона в атоме водорода,
![]()
где
![]() величина,
совпадающая с первым боровским радиусом.
величина,
совпадающая с первым боровским радиусом.
Вероятность обнаружить электрон в атоме водорода, находящемся в
![]() состоянии,
в интервале от
состоянии,
в интервале от
![]() до
до![]()
![]()
Спин (собственный механический момент импульса) электрона
![]()
где
![]() магнитное
спиновое квантовое число
магнитное
спиновое квантовое число![]()
Коротковолновая граница сплошного рентгеновского спектра
![]()
где
![]() заряд
электрона;
заряд
электрона;![]() разность
потенциалов, приложенная к рентгеновской
трубке.
разность
потенциалов, приложенная к рентгеновской
трубке.
![]() Закон
Мозли, определяющий частоты спектральных
линий
Закон
Мозли, определяющий частоты спектральных
линий
характеристического рентгеновского излучения,
![]()
где
![]() постоянная
Ридберга;
постоянная
Ридберга;![]() порядковый
номер элемента в периодической системе;
порядковый
номер элемента в периодической системе;![]() постоянная
экранирования;
постоянная
экранирования;![]() определяет рентгеновскую серию
определяет рентгеновскую серию![]() определяет
линии соответствующей серии
определяет
линии соответствующей серии![]() .
.
Семестровые задания
31.1. Написать уравнение Шредингера для электрона, находящегося в водородном атоме.
31.2. Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид
![]()
где
![]() —
некоторая
постоянная,
—
некоторая
постоянная,
![]() —
первый боровский радиус. Найти для
основного состояния атома водорода
наиболее вероятное расстояние электрона
от ядра.
—
первый боровский радиус. Найти для
основного состояния атома водорода
наиболее вероятное расстояние электрона
от ядра.
31.3. Волновая функция, описывающая движение электрона в основном
состоянии атома водорода, имеет вид
![]()
где
![]() — некоторая
постоянная;
— некоторая
постоянная;
![]() — первый
боровский радиус. Найти для основного
состояния атома водорода среднее
значение
— первый
боровский радиус. Найти для основного
состояния атома водорода среднее
значение
![]() кулоновской силы.
кулоновской силы.
31.4. Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид
![]()
где
![]() — некоторая
постоянная;
— некоторая
постоянная;
![]() — первый
боровский радиус. Найти для основного
состояния атома водорода среднее
значение
— первый
боровский радиус. Найти для основного
состояния атома водорода среднее
значение
![]() потенциальной энергии.
потенциальной энергии.
31.5.
Определить с помощью уравнения Шредингера
энергию электрона, находящегося в атоме
водорода в состоянии
![]() ,
где A,
а
и
- некоторые постоянные.
,
где A,
а
и
- некоторые постоянные.
31.6.
Волновая функция
![]() определена только в области
определена только в области![]() .
Используя условие нормировки, определить
нормировочный множитель А.
.
Используя условие нормировки, определить
нормировочный множитель А.
31.7.
Волновая функция, описывающая 1s
– состояние электрона в атоме водорода,
имеет вид
![]() ,
гдеr
– расстояние электрона от ядра, a0
– первый
боровский радиус. Определить нормированную
волновую функцию, отвечающую этому
состоянию.
,
гдеr
– расстояние электрона от ядра, a0
– первый
боровский радиус. Определить нормированную
волновую функцию, отвечающую этому
состоянию.
31.8.
Собственная функция, описывающая
основное состояние электрона в атоме
водорода, имеет вид
![]() где
где![]() (боровский радиус). Определить расстояние
(боровский радиус). Определить расстояние![]() на котором вероятность нахождения
электрона максимальна.
на котором вероятность нахождения
электрона максимальна.
31.9.
Электрон в атоме водорода описывается
в основном состоянии волновой функцией
![]() Определить отношение вероятностей
Определить отношение вероятностей![]() пребывания электрона в сферических
слоях толщиной
пребывания электрона в сферических
слоях толщиной![]() и радиусами
и радиусами![]() и
и![]() .
.
31.10.
Зная, что нормированная собственная
волновая функция, описывающая основное
состояние электрона в атоме водорода,
имеет вид
![]() найти
среднее расстояние
найти
среднее расстояние![]() электрона от ядра.
электрона от ядра.
