
А и Г 704 рус
.doc$$$ 1
Определитель
второго порядка
![]() равен:
равен:
$$$ 2
Определитель
третьего порядка
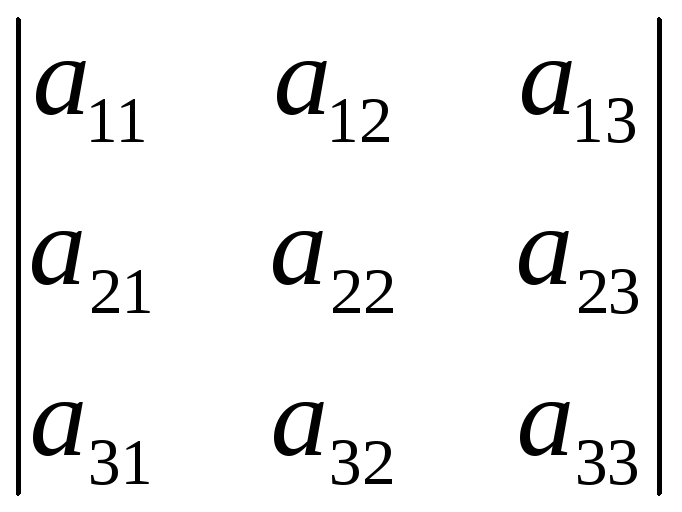 равен:
равен:
$$$ 3
Если в определителе поменять местами две строки, то он
$$$ 4
Если
какуюлибо строку
определителя
![]() -го
порядка умножить на число
-го
порядка умножить на число
![]() ,
то значение определителя
,
то значение определителя
$$$ 5
Если соответствующие элементы двух строк определителя равны, то он
$$$ 6
Если
к элементам какойлибо
строки определителя
![]() -го
порядка прибавить соответствующие
элементы другой строки, умноженные на
число
-го
порядка прибавить соответствующие
элементы другой строки, умноженные на
число
![]() ,
то определитель
,
то определитель
$$$ 7
Если определитель содержит нулевую строку, то он равен
$$$ 8
Если определитель содержит нулевой столбец, то он равен
$$$ 9
Если в определителе поменять местами два столбца, то он
$$$ 10
Если элементы какой-либо строки определителя содержат общий множитель, то
$$$ 11
Если соответствующие элементы двух столбцов определителя равны, то он
$$$ 12
Если
![]() –
минор элемента
–
минор элемента
![]() ,
то алгебраическое дополнение этого
элемента равно
,
то алгебраическое дополнение этого
элемента равно
$$$ 13
Если
элементы какого-либо столбца определителя
![]() -го
порядка умножить на число k, то значение
определителя
-го
порядка умножить на число k, то значение
определителя
$$$ 14
Если все строки определителя заменить соответствующими столбцами, то от этого определитель
$$$ 15
Если соответствующие элементы двух параллельных рядов определителя пропорциональны, то он
$$$ 16
Для
умножения матрицы
![]() на число
на число
![]() необходимо:
необходимо:
$$$ 17
Если
матрица
![]() размерности
размерности
![]() и матрица
и матрица
![]() размерности
размерности
![]() ,
то произведение матриц
,
то произведение матриц
![]() и
и
![]() возможно при условии:
возможно при условии:
$$$ 18
Если
![]() единичная матрица, а матрица
единичная матрица, а матрица
![]() является обратной к квадратной матрице
является обратной к квадратной матрице
![]() ,
то
,
то
$$$ 19
Если
определитель матрицы
 не равен нулю, то матрица
не равен нулю, то матрица
![]() ,
обратная к
,
обратная к
![]() вычисляется по формуле
вычисляется по формуле
$$$ 20
Рангом
матрицы
![]() называется
называется
$$$ 21
Квадратная матрица называется невырожденной, если
$$$ 22
Квадратная матрица называется единичной, если у нее
$$$ 23
Минором
![]() элемента
элемента
![]() определителя
определителя
![]() называется:
называется:
$$$ 24
Ранг матрицы не изменится, если
$$$ 25
Ранг матрицы не изменится, если
$$$ 26
Если А – квадратная матрица, а Е – единичная матрица такой же размерности, то
$$$ 27
Ранг матрицы не изменится, если
$$$ 28
Ранг матрицы не изменится, если
$$$ 29
Ранг матрицы не изменится, если
$$$ 30
Матрицы
![]() размерности
размерности
![]() и
и
![]() размерности
размерности
![]() называются равными, если
называются равными, если
$$$ 31
Сложение
матриц А размерности
![]() и В размерности
и В размерности
![]() возможно, если
возможно, если
$$$ 32
Суммой
матриц одинаковой размерности
![]() и
и
![]() называется матрица
называется матрица
![]() ,
элементы которой определяются по формуле
,
элементы которой определяются по формуле
$$$ 33
Матрица
![]() ,
полученная из матрицы А путем замены
ее строк столбцами с теми же номерами
называется
,
полученная из матрицы А путем замены
ее строк столбцами с теми же номерами
называется
$$$ 34
Если
определитель системы
![]() линейных однородных уравнений с
линейных однородных уравнений с
![]() неизвестными не равен нулю, то система
неизвестными не равен нулю, то система
$$$ 35
Если
определитель основной матрицы системы
![]() линейных неоднородных уравнений с
линейных неоднородных уравнений с
![]() неизвестными не равен нулю, то она
неизвестными не равен нулю, то она
$$$ 36
Система линейных уравнений называется совместной, если она
стных
$$$ 37
Система линейных уравнений называется несовместной, если она
$$$ 38
Система линейных уравнений называется однородной, если
$$$ 39
Для того чтобы система m линейных уравнений с n неизвестными была совместной, необходимо и достаточно, чтобы
$$$ 40
Если
![]() –
не равный нулю определитель основной
матрицы системы n уравнений
с n неизвестными, а
–
не равный нулю определитель основной
матрицы системы n уравнений
с n неизвестными, а
![]() –
определитель, полученный из
–
определитель, полученный из
![]() заменой j-го столбца
столбцом свободных членов, то решение
системы находится по формулам
заменой j-го столбца
столбцом свободных членов, то решение
системы находится по формулам
$$$ 41
Если А – основная матрица системы линейных уравнений невырожденная, а В – матрица-столбец свободных членов, то решение системы Х – матрица-столбец неизвестных находится по формуле
$$$ 42
Для системы m линейных уравнений с n неизвестными (Ax=B) применим матричный метод решения, если
$$$ 43
Вычислить:

$$$ 44
Вычислить:
![]()
$$$ 45
Вычислить
![]()
$$$ 46
Вычислить:
$$$ 47
Вычислить:![]()
$$$ 48
Вычислить:![]()
$$$ 49
Вычислить:![]()
$$$ 50
Вычислить:
$$$ 51
Вычислить:
$$$ 52
Вычислить:![]()
$$$ 53
Найти
алгебраическое дополнение
![]() определителя
определителя

$$$ 54
Найти
алгебраическое дополнение
![]() определителя
определителя

$$$ 55
Найти
алгебраическое дополнение
![]() определителя
определителя

$$$ 56
Найти
алгебраическое дополнение
![]() определителя
определителя

$$$ 57
Найти
алгебраическое дополнение
![]() определителя
определителя

$$$ 58
Найти
произведение матриц
![]() и
и
![]() ,
если
,
если
![]() .
.
$$$ 59
Найти
ранг матрицы
 .
.
$$$ 60
Найти
ранг матрицы
![]()
$$$ 61
Вычислить
![]() ,
если
,
если
![]() ;
;

$$$ 62
Найти
![]() ,
если
,
если
![]() и
и
![]()
$$$ 63
Найти
![]() ,
если
,
если
![]() и
и
![]()
$$$ 64
Найти
![]() ,
если
,
если
![]() ;
;

$$$ 65
Найти
![]() ,
если
,
если
![]() ;
;

$$$ 66
Решить
систему однородных уравнений
 .
.
$$$ 67
Решить
систему уравнений
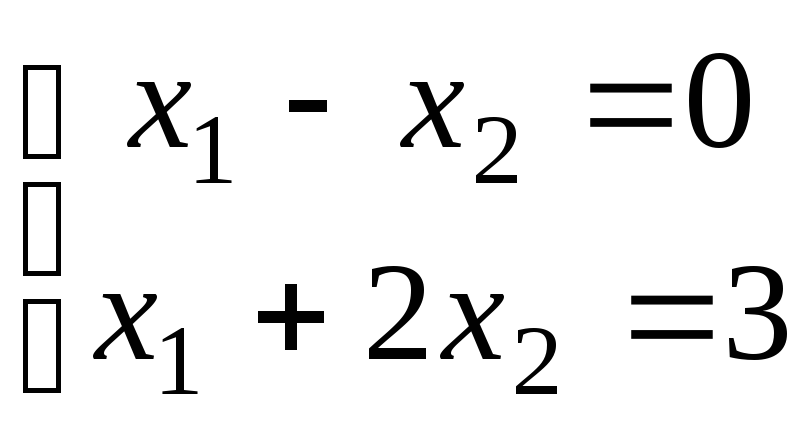
$$$ 68
Решить
систему уравнений:

$$$ 69
Решить
систему уравнений:

$$$ 70
Решить
систему уравнений:

$$$ 71
Решить
систему уравнений:

$$$ 72
Решить
систему уравнений:

$$$ 73
 .
Найти
.
Найти
![]()
$$$ 74
![]() ,
,
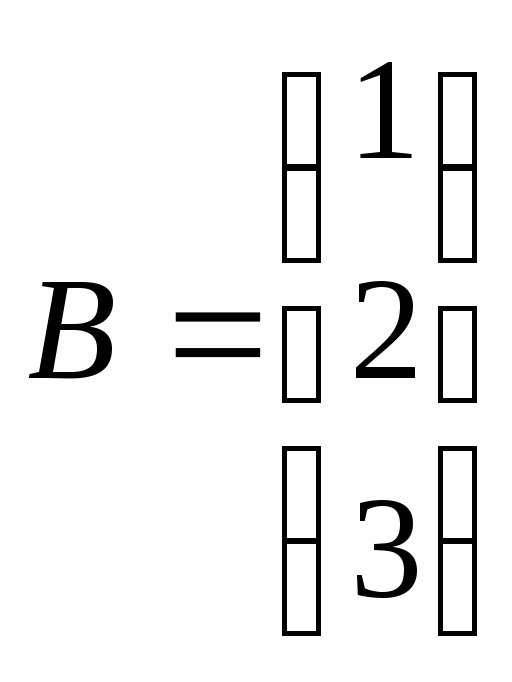 Найти АВ
Найти АВ
$$$ 75 Вычислить определитель

$$$ 76
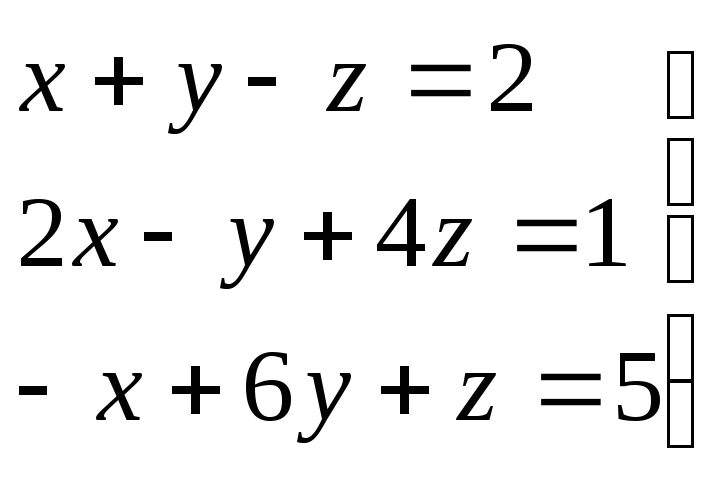 .
Найти
.
Найти
![]()
$$$ 77
При каком условии существует обратная матрица?
$$$ 78
![]() .
Найти
.
Найти
![]()
$$$ 79
![]() Найти
Найти
![]()
$$$ 80
 .
Найти
.
Найти
![]()
$$$ 81
 .
Найти
.
Найти
![]()
$$$ 82
 .
Вычислить минор
.
Вычислить минор
![]()
$$$ 83
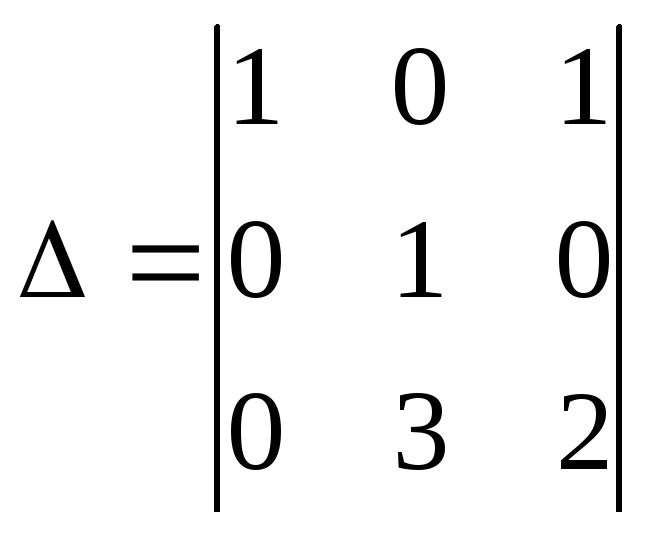 .
Вычислить алгебраическое
дополнение
.
Вычислить алгебраическое
дополнение
![]()
$$$ 84
![]() ,
,
 .
Найти произведение
.
Найти произведение![]()
$$$ 85
$$$ 86
![]() ,
,
 .
Найти произведение
.
Найти произведение
![]()
$$$ 87
![]() .
Найти
.
Найти
![]()
$$$ 88
![]() .
Найти
.
Найти
![]()
$$$ 89
![]() .
Найти
.
Найти
![]()
$$$ 90
![]() .
Найти
.
Найти
![]()
$$$ 91
![]() .
Найти
.
Найти
![]()
$$$ 92
![]() .
Найти
.
Найти
![]()
$$$ 93
![]() .
Найти
.
Найти
![]()
$$$ 94
Вычислить
определитель
![]()
$$$ 95
Вычислить
определитель
![]()
$$$ 96
Вычислить
определитель
![]()
$$$ 97
Вычислить
определитель
![]()
$$$ 98
![]() .
Найти
.
Найти
![]()
$$$ 99
 .
Найти
.
Найти
![]()
$$$ 100
 при
каком значении
при
каком значении
![]() система имеет единственное решение
система имеет единственное решение
$$$ 101
 при
каком значении
при
каком значении
![]() система имеет единственное решение
система имеет единственное решение
$$$ 102
![]() при
каком значении
при
каком значении
![]() существует обратная матрица
существует обратная матрица
$$$ 103
 для
элемента
для
элемента
![]() вычислить алгебраическое дополнение
вычислить алгебраическое дополнение
![]()
$$$ 104
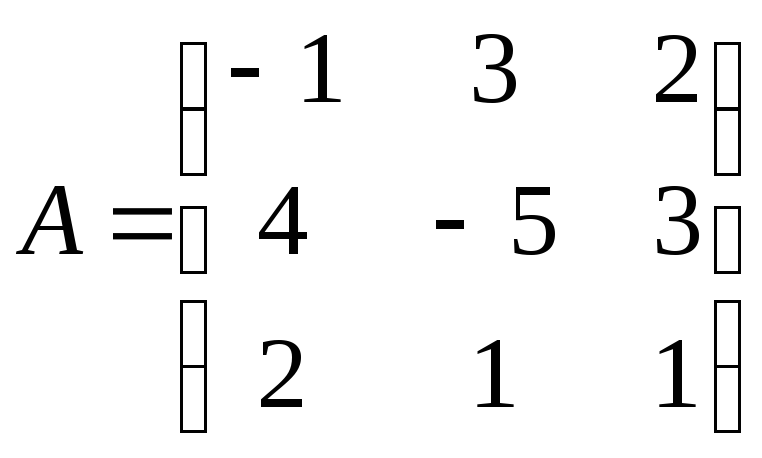 для
элемента
для
элемента
![]() вычислить алгебраическое дополнение
вычислить алгебраическое дополнение
![]()
$$$ 105
Векторы называются равными, если они
$$$ 106
Векторы
![]() и
и
![]() коллинеарны, если:
коллинеарны, если:
$$$ 107
Произведением
вектора
![]() на число
на число
![]() называется вектор
называется вектор
![]() ,
удовлетворяющий условиям:
,
удовлетворяющий условиям:
$$$108
Если
векторы
![]() и
и
![]() коллинеарны
коллинеарны
![]() ,
тогда найдется число
,
тогда найдется число
![]() ,
удовлетворяющее:
,
удовлетворяющее:
$$$ 109
Если
векторы
![]() и
и
![]() образуют базис на плоскости, то найдутся
такие числа
образуют базис на плоскости, то найдутся
такие числа
![]() ,
что любой вектор
,
что любой вектор
![]() можно представить в виде:
можно представить в виде:
$$$ 110
Если
векторы
![]() не компланарны, то выполняется условие:
не компланарны, то выполняется условие:
$$$ 111
Если
векторы
![]() образуют базис в пространстве, то
найдутся такие числа
образуют базис в пространстве, то
найдутся такие числа
![]() ,
что любой вектор
,
что любой вектор
![]() можно представить в виде:
можно представить в виде:
$$$ 112
Векторное
произведение векторов
![]() и
и
![]() равно:
равно:
$$$ 113
Проекция
вектора
![]() на ось
на ось
![]() равна
равна
$$$ 114
Скалярное
произведение векторов
![]() и
и
![]() равно
равно
$$$ 115
Скалярное
произведение вектора
![]() на сумму векторов
на сумму векторов
![]() и
и
![]() равно:
равно:
$$$ 116
Проекция
вектора
![]() на ось
на ось
![]() (
(![]() число) равна
число) равна
$$$ 117
Скалярное
произведение векторов
![]() ,
т.е.
,
т.е.
![]() равно
равно
$$$ 118
Векторным
произведением векторов
![]() и
и
![]() называется вектор, удовлетворяющий
условиям
называется вектор, удовлетворяющий
условиям
$$$ 119
Указать
необходимое и достаточное условие
ортогональности векторов
![]() и
и
![]()
$$$ 120
Расстояние
между точками
![]() и
и
![]() определяется
формулой:
определяется
формулой:
$$$ 121
Указать
необходимое и достаточное условие
коллинеарности векторов
![]() и
и
![]()
$$$ 122
Смешанное
произведение векторов
![]()
![]()
![]() равно:
равно:
$$$ 123
Для
векторного произведения векторов
![]() и
и
![]() справедливо
свойство:
справедливо
свойство:
$$$ 124
Указать
необходимое и достаточное условие
компланарности векторов
![]() и
и
![]() :
:
$$$ 125
Векторы называются коллинеарными, если они
$$$ 126
Векторы называются компланарными, если они
$$$ 127
Если
![]() ,
то
,
то
![]() равно
равно
$$$ 128
Если
![]() ,
то
,
то
![]() равно
равно
$$$ 129
Проекция
вектора
![]() на вектор
на вектор
![]() равна
равна
$$$ 130
Проекция
вектора
![]() на вектор
на вектор
![]() равна
равна
$$$ 131
Модуль
векторного произведения векторов
![]() равен
равен
$$$ 132
Вектор,
равный векторному произведению векторов
![]() ,
направлен
,
направлен
$$$ 133
Найти
скалярное произведение векторов
![]() ,
если
,
если
![]()
$$$ 134
Найти
![]() ,
если
,
если
![]()
$$$ 135
Найти
модуль вектора
![]() ,
если заданы точки
,
если заданы точки
![]() и
и
![]()
$$$ 136
Найти
![]() ,
если даны коллинеарные векторы
,
если даны коллинеарные векторы
![]() и
и
![]() .
.
$$$ 137
Найти
![]() ,
если даны:
,
если даны:
![]() .
.
$$$ 137
Найти
площадь параллелограмма, построенного
на векторах
![]() и
и
![]() ,
если
,
если
![]()
$$$ 138
Найти
![]() ,
если даны:
,
если даны:
![]()
$$$ 139
Найти
![]() ,
если даны:
,
если даны:
![]() .
.
$$$ 140
Найти
![]() ,
если даны:
,
если даны:
![]()
![]()
![]() .
.
$$$ 141
Найти
объем параллелепипеда, построенного
на векторах
![]()
$$$ 142
Найти
скалярное произведение векторов
![]()
$$$ 143
Найти
единичный вектор
![]() вектора
вектора
![]()
$$$ 144
Определить
модуль суммы векторов
![]()
$$$ 145
Найти
сумму векторов
![]()
$$$ 146
Найти
сумму векторов
![]()
$$$ 147
Найти
произведение вектора
![]() на
число
на
число
![]()
$$$ 148
Найти
разность векторов
![]()
$$$ 149
Найти
сумму векторов
![]()
$$$ 150
Найти
модуль вектора
![]()
$$$ 151
Найти
скалярное произведение векторов
![]()
$$$ 152
Найти
смешанное произведение векторов
![]()
$$$ 153
Найти
векторное произведение векторов
![]()
$$$ 154
Найти
скалярное произведение векторов
![]()
$$$ 155
Найти
единичный вектор вектора
![]()
$$$ 156
Определить
модуль суммы векторов
![]()
$$$ 157
Найти
сумму векторов
![]()
$$$ 158
Найти
скалярное произведение векторов
![]()
$$$ 159
Найти
смешанное произведение векторов
![]()
$$$ 160
Найти
![]() ,
если векторы
,
если векторы
![]() и
и
![]() ортогональны и
ортогональны и
![]() .
.
$$$ 161
Уравнение
прямой, проходящей через точку М![]() ,
с угловым коэффициентом
,
с угловым коэффициентом
![]() ,
имеет вид
,
имеет вид
$$$ 162
Уравнение
прямой, проходящей через две точки:
![]() и
и
![]() ,
имеет вид:
,
имеет вид:
