
050703, 050704 Мамандақтарына арналған (2-семестр)
1-модуль
$$$ 1
![]() мен
мен
![]() жиындарының бірігуін көрсетіңіз
жиындарының бірігуін көрсетіңіз
C={x:
x![]() A
немесе x
A
немесе x![]() B}
$$$
2
B}
$$$
2
![]() мен
мен
![]() жиындарының қиылысуын көрсетіңіз
жиындарының қиылысуын көрсетіңіз
C={x:
x![]() A
және x
A
және x![]() B}
$$$ 3
B}
$$$ 3
![]() мен
мен
![]() жиындарының айырымын көрсетіңіз
жиындарының айырымын көрсетіңіз
C={x:
x![]() A
және x
A
және x![]() B}
$$$ 4
B}
$$$ 4
Егер
U-негізгі жиын,
![]() болса, онда
болса, онда
D)
![]() $$$ 5
$$$ 5
Егер
U-негізгі жиын,
![]() болса, онда
болса, онда
![]()
$$$ 6
Егер
U-негізгі жиын,
![]() болса, онда
болса, онда
![]() $$$
7
$$$
7
Егер
U-негізгі
жиын,
![]() болса, онда
болса, онда
B)
![]() $$$ 8
$$$ 8
A={2,
-3, 0, a, б, в} мен B={-1, 0, 4, в} жиындарының
бірігуін көрсетіңіз.
![]()
C) {2, -3, 0, а, б, в, -1, 4} $$$ 9
A={2,
-3, 0, a, б, в} мен B={-1, 0, 4, в} жиындарының
қиылысуын көрсетіңіз.
![]()
D) {0, в} $$$ 10
A={2,
-3, 0, a, б, в}
мен B={-1, 0, 4, в}
жиындарының айырымын
көрсетіңіз.
![]()
E) {2, -3, а, б}
$$$ 11
![]() нақты
санының
маңайын көрсетіңіз (
>0):
нақты
санының
маңайын көрсетіңіз (
>0):
A)
{x![]() R:
a-
< x < a+}
$$$
12
R:
a-
< x < a+}
$$$
12
![]() нақты
санының оң жақ
маңайын көрсетіңіз (
>0):
нақты
санының оң жақ
маңайын көрсетіңіз (
>0):
B)
{x![]() R:
a ≤ x < a+}
$$$
13
R:
a ≤ x < a+}
$$$
13
![]() нақты
санының сол жақ
маңайын көрсетіңіз (
>0):
нақты
санының сол жақ
маңайын көрсетіңіз (
>0):
C)
{x![]() R:
a-
< x ≤ a}
$$$ 14
R:
a-
< x ≤ a}
$$$ 14
a= +∞ (плюс ақырсыздық) нүктесінің маңайын көрсетіңіз ( >0):
D) (, +∞] $$$ 15
a= -∞ (минус ақырсыздық) нүктесінің маңайын көрсетіңіз ( >0):
E) [-∞; -)
$$$ 16
a= ∞ (ақырсыздық) нүктесінің маңайын көрсетіңіз ( >0):
A)
[-∞; -)
![]() (;
+∞]
$$$ 17
(;
+∞]
$$$ 17
Егер X-жоғарыдан шенелген жиын, ал M оның жоғарғы шекарасы болса, онда
B)
![]() $$$ 18
$$$ 18
Егер X-төменнен шенелген жиын, ал m оның төменгі шекарасы болса, онда
C)
![]() $$$ 19
$$$ 19
Егер
X-шенелген
жиын болса, онда
![]()
D)
![]()
$$$ 20
Егер M саны X-cандар жиынының ең үлкен элементі болса, онда
![]()
$$$ 21
Егер m саны X-cандар жиынының ең кіші элементі болса, онда
A)
![]() $$$
22
$$$
22
X жиынының дәл жоғарғы шекарасы мына түрде белгіленеді:
![]() $$$
23
$$$
23
X жиынының дәл төменгі шекарасы мына түрде белгіленеді:
C)
![]() $$$ 24
$$$ 24
Егер
X=[1;2) болса, онда
![]()
D)2
$$$ 25
Егер
X=[1;2) болса, онда
![]() табыңыз
табыңыз
![]() жоқ
жоқ
$$$ 26
Егер
X=(2;3] болса, онда
![]()
A) 2 $$$ 27
Егер
X=(2;3) болса, онда
![]() және
және![]() табыңыз
табыңыз
B)
![]() -жоқ;
-жоқ;![]() 2
$$$ 28
2
$$$ 28
Егер X=(2;3] болса, онда
C) maxX=supX=3
$$$ 29
Егер y=f(x) функциясы D аймағында (қатаң) өспелі болса, онда
D)
![]()
$$$ 30
Егер y=f(x) функциясы D аймағында (қатаң) кемімелі болса, онда
E)
![]()
$$$ 31
Егер y=f(x) функциясы D аймағында кемімейтін болса, онда
A)
![]()
$$$ 32
Егер y=f(x) функциясы D аймағында өспейтін болса, онда
B)
![]()
$$$ 33
Егер
|q|<1 болса, онда
![]()
C) 0
$$$ 34
Егер
|q|>1 болса, онда
![]()
D) ∞
$$$ 35
![]()
E) шек жоқ
$$$ 36
Егер
![]() және
және
![]() болса, онда
болса, онда![]()
A) 2
$$$ 37
![]()
B) -∞
$$$ 38
![]()
C) +∞
$$$ 39
![]()
D) 1
$$$ 40
![]()
E) -1
$$$ 41
![]()
A) 1
$$$ 42
![]()
B) -∞
$$$ 43
![]()
C) +∞
$$$ 44
Åãåð
![]() тең болса,
онда
тең болса,
онда
À)
![]()
Â)
![]()
Ñ)
![]() функциясы
функциясы
![]() функциясына салыстыр¹анда аºырсыз аз;
функциясына салыстыр¹анда аºырсыз аз;
D)
![]() ïåí
ïåí
![]() функциялары,
функциялары,
![]() ұмтылғанда, эквивалентті;
ұмтылғанда, эквивалентті;
;
Å)
![]() функциясы
функциясы
![]() функциясына салыстыр¹анда аºырсыз
¾лкен.
функциясына салыстыр¹анда аºырсыз
¾лкен.
$$$ 45
Åãåð
![]() болса, онда
болса, онда
À)
![]() 0
.
0
.
Â)
![]()
![]() ;
;
Ñ)
![]()
![]() ;
;
D)
![]()
![]() ;
;
Å)
![]()
![]() ;
;
$$$46
Егер
![]() ,
,
![]() -ақырлы
сан болса, онда:
-ақырлы
сан болса, онда:
A)
![]() -нүктесінің
қандайда бір манайында
-нүктесінің
қандайда бір манайында
![]() шенелген функция
шенелген функция
B)
![]() -
нүктесінің кез-келген манайында
-
нүктесінің кез-келген манайында
![]() шенелген функция
шенелген функция
C)
![]() -нүктесінде
-нүктесінде
![]() функциясы анықталған
функциясы анықталған
D)
![]()
E)
![]() -
нүктесінде
-
нүктесінде
![]() үзіліссіз функция
үзіліссіз функция
$$$47
Егер
![]() біржақты шектері бар, бірақ
біржақты шектері бар, бірақ
![]() теңдіктерінің ең болмағанда біреуі
орындалмаса, онда
теңдіктерінің ең болмағанда біреуі
орындалмаса, онда
![]() функциясы
функциясы
![]() нүктесінде
нүктесінде
A)2 текті үзілісті
B) 1 текті үзілісті
C) ақырсыз үлкен
D) ақырсыз кішкене
E) үзіліссіз
деп аталады.
$$$48
Егер
![]() -тізбегі
шенелген, ал
-тізбегі
шенелген, ал
![]() -ақырсыз
үлкен тізбек болса, онда:
-ақырсыз
үлкен тізбек болса, онда:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$49
![]() шегі
бар болуы үшін
келесі шарттың:
шегі
бар болуы үшін
келесі шарттың:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
орындалуы, қажетті және жеткілікті
$$$50
Егер
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
теңдігі
орындалса, онда
![]() функциясы
функциясы
![]() нүктесінде
үзіліссіз деп аталады
нүктесінде
үзіліссіз деп аталады
$$$51
Егер
![]() нүктесіндегі
нүктесіндегі
![]() функциясының біржақты шектерінің ең
болмағанда біреуі жоқ немесе ақырсыз
болса, онда
функциясының біржақты шектерінің ең
болмағанда біреуі жоқ немесе ақырсыз
болса, онда
![]() нүктесінде
нүктесінде
![]() функциясы
функциясы
A) екінші текті үзілісті
B) бірінші текті үзілісті
C) шенелген
D) шенелмеген
E) үзіліссіз
деп аталады
$$$52
Егер
![]() және
және
![]() үшін
үшін
![]() болса, онда:
болса, онда:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$53
I-ші тамаша шекті көрсетіңіз:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$54
II- ші тамаша шекті көрсетіңіз:
A)

B)

C)
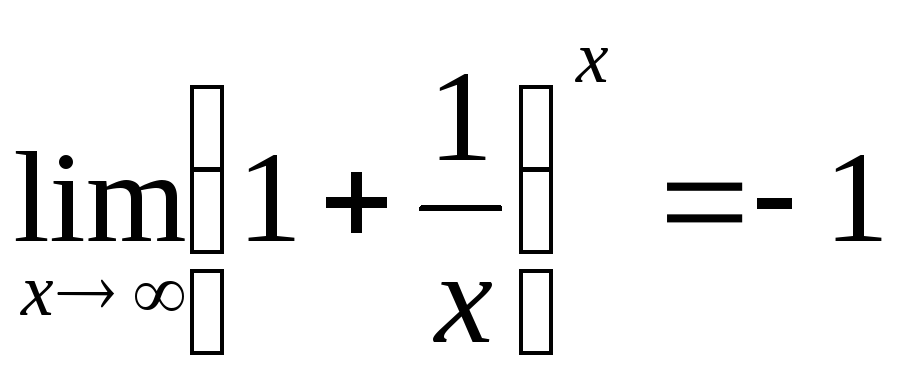
D)

E)

$$$55
![]() функциясының
үзіліс нүктесін тауып, нүктенің сипатын
анықтаңыз:
функциясының
үзіліс нүктесін тауып, нүктенің сипатын
анықтаңыз:
A) үзіліс нүктесі жоқ
B)
![]() бірінші текті үзіліс нүктесі
C)
бірінші текті үзіліс нүктесі
C)
![]() екінші текті үзіліс нүктесі
екінші текті үзіліс нүктесі
D)
![]() бірінші
текті үзіліс нүктесі
бірінші
текті үзіліс нүктесі
E)
![]() екінші текті үзіліс нүктесі
екінші текті үзіліс нүктесі
$$$56
Егер
![]() -сандық
тізбек жинақты болса, онда ол:
-сандық
тізбек жинақты болса, онда ол:
A) шенелген
B) шенемелген
C) монотонды
D) нөлге тең
E) ақырсыз үлкен шама
$$$57
Шекті
табыңыз:
![]() .
.
A) 0
B) 2
C) 1
D) жоқ
E) 3
$$$58
Шекті
табыңыз:
![]()
A) 0
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$59
Шекті
табыңыз:
![]()
A)
![]()
B)
![]()
C) 6
D)
![]()
E)
![]()
$$$60
Шекті
табыңыз:
![]() .
.
A) 7
B) 3
C) 1
D) 0
E)
![]()
$$$61
Шекті
табыңыз:
![]() .
.
A)
![]()
B)
![]()
C) 2
D) 0
E)
![]()
$$$ 62
![]()
А)
![]()
В)12 ;
C)
![]() ;
;
D) øåãi æîº;
Å)
![]() .
.
$$$ 63
![]()
A) 8 ;
B)
![]() ;
;
C)
![]()
![]() ;
;
D)
![]() ;
;
E)
![]() .
.
$$$ 64
![]()
A)5;
B)
![]() ;
;
C) 12;
D) 0;
E)
![]() .
.
$$$ 65
![]()
À) 4;
Â) 1;
Ñ) 4;
D) 3;
Å) –3;
$$$ 66
![]()
À)
![]() ;
;
Â)
![]() ;
;
Ñ) 0;
D)
![]() ;
;
Å)
![]() .
.
$$$ 67
![]()
À)0 ;
B)
![]() ;
;
C)1;
D)
![]() ;
;
Å) øåãi æîº.
$$$ 68
![]()
A)![]()
B)
![]() ;
;
C)1;
D)
![]() ;
;
E) 2.
$$$ 69
![]()
A) 3 ;
B)
![]() ;
;
C)0;
D)
![]() ;
;
E)
![]() .
.
$$$ 70
![]()
À) 1;
Â) 0;
Ñ)
![]() ;
;
D) 2;
Å) -1.
$$$ 71
![]()
À)-1;
Â) 0;
Ñ) 1;
D)
![]() ;
;
Å) 2.
$$$ 72
![]()
À)
![]() ;
;
Â)
![]() ;
;
Ñ) 1;
D)
![]() ;
;
Å)
![]() .
.
$$$73
![]()
À) 3 ;
Â) 6;
Ñ)
![]() ;
;
D) 1;
Å)0 .
$$$ 74
![]()
À)
![]() ;
;
Â) 1;
Ñ) ;
D)
![]() ;
;
Å) øåãi æîº.
$$$ 75
![]()
A)
-![]() ;
;
B)
![]() ;
;
C)
![]() ;
;
D) øåãi æîº;
E)1.
$$$ 76
![]()
À)1;
Â) 2;
Ñ) 0;
D)
![]() ;
;
Å)
![]() .
.
$$$ 77
Шекті
табыңыз:
![]()
А) 2
В)
![]()
С) 3
Д) -4
Е) шегі жоқ
$$$ 78
Шекті
табыңыз:
![]()
А)
![]()
В) 2
С) 0
Д) -4
Е) шегі жоқ
$$$ 79
Шекті
табыңыз:
![]()
А) -4
В) 2
С)
![]()
Д)0
Е) шегі жоқ
$$$ 80
Шекті
табыңыз:
![]()
А) шегі жоқ
В)
![]()
С) 3
Д) -4
Е) 2
$$$ 81
Шекті
табыңыз:
![]()
А) 5
В)
![]()
С) 3
Д) -4
Е) шегі жоқ
$$$ 82
Шекті
табыңыз:
![]()
А) 2
В)
![]()
С) 3
Д) -4
Е) шегі жоқ
$$$ 83
Шекті
табыңыз:
![]()
А) 3
В) 2
С)
![]()
Д) -4
Е) шегі жоқ
$$$ 84
Шекті
табыңыз:
![]()
А) -4
В)
![]()
С) 3
Д)0
Е) шегі жоқ
$$$85
 шегін
табыңыз:
шегін
табыңыз:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E) 3
$$$86
 шегін
табыңыз:
шегін
табыңыз:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$ 87
![]() функциясыны»
x
н¾ктесiндегi
туындысыны» аныºтамасы
функциясыны»
x
н¾ктесiндегi
туындысыны» аныºтамасы
![]()
À)
![]() ;
;
Â)
![]() ;
;
Ñ)
![]() ;
;
D)
![]() ;
;
Å)
![]()
$$$ 88
Êåç-келген
![]() ñàíû ¾øií
ñàíû ¾øií![]()
À)
![]() ;
;
Â)
![]() ;
;
Ñ)
![]() ;
;
D)
![]() ;
;
E)
![]() .
.
$$$ 89
Б¼лшектi»
туындысы
![]()
 ;
;
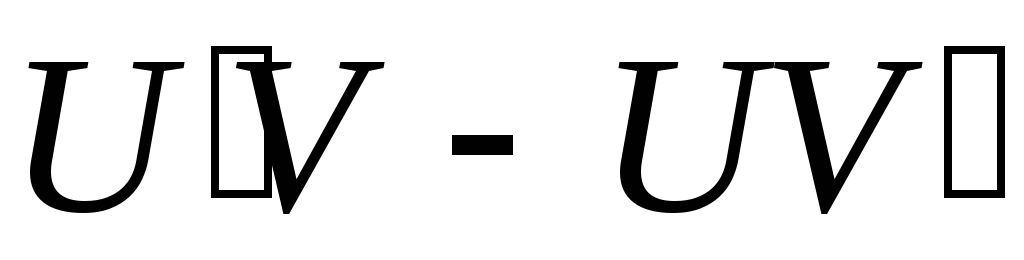 ;
;
C)
 ;
;
D)
![]() ;
;
E)
![]() .
.
$$$ 90
![]()
À)
![]()
B)
![]() ;
;
C)
![]() ;
;
D)
![]() ;
;
E)
![]()
![]()
$$$ 91
![]()
A)
![]() ;
;
B)
![]() ;
;
C)
![]() ;
;
D)
![]() ;
;
E)
![]() .
.
$$$ 92
![]()
A)
![]() ;
;
B)
![]() ;
;
C)
-![]() ;
;
D)
![]() ;
;
E)
![]() .
.
$$$ 93
![]()
À)
![]() ;
;
Â)
![]() ;
;
Ñ)
![]() ;
;
D)
![]() ;
;
Å)
![]() .
.
$$$ 94
![]()
À)
![]() ;
;
Â)
![]() ;
;
Ñ)
![]() ;
;
D)
![]() ;
;
Å)
![]() .
.
$$$ 95
![]()
À)
![]() ;
;
Â)
![]() ;
;
Ñ)
![]() ;
;
D)
![]() ;
;
Å)
![]() .
.
$$$ 96
![]() ¾øií
¾øií
![]()
À)
![]() ;
;
Â)
![]() ;
;
Ñ)
![]() ;
;
D)
![]() ;
;
Å)
![]() .
.
$$$ 97
![]()
A)
![]() ;
;
B)
![]() ;
;
C)
![]() ;
;
D)
![]() ;
;
E) 0.
$$$ 98
![]()
À)
![]() ;
;
Â)
![]() ;
;
Ñ)
![]() ;
;
D)
![]() ;
;
Å) 2.
$$$ 99
![]() .
.
![]()
A)
![]() ;
;
B)
![]() ;
;
C)
![]() ;
;
D)
![]() ;
;
E)
![]() .
.
$$$ 100
![]()
![]()
À)
![]() ;
;
B)
![]() ;
;
C)
![]() ;
;
D)
![]() ;
;
Å)
![]() .
.
$$$ 101
![]()
![]()
A)
![]() ;
;
B)
![]() ;
;
C)
![]() ;
;
D)
![]() ;
;
E)
![]() .
.
$$$ 102
![]()
![]()
A)
![]() ;
;
B)
![]() ;
;
C)
![]() ;
;
D)
![]() ;
;
E)
![]() .
.
$$$ 103
![]()
À)
![]() ;
;
Â)
![]() ;
;
Ñ)
![]() ;
;
D)
![]() ;
;
Å)
![]() .
.
$$$ 104
![]()
À)
![]() ;
;
Â)
![]() ;
;
Ñ)
![]() ;
;
D)
![]()
Å)
![]() .
.
$$$ 105
![]() áåðiëãåí
áåðiëãåí
![]()
À)
![]() .
;
.
;
Â)
![]() ;
;
Ñ)
![]() ;
;
D)
![]() ;
;
Å)
![]()
$$$ 106
![]()
À)
![]() ;
;
Â)![]() ;
;
Ñ)![]() ;
;
D)
![]() ;
;
Å)
![]() .
.
$$$ 107
![]()
À)
![]() ;
;
Â)
![]() ;
;
Ñ)
![]() ;
;
D)
![]() ;
;
Å)
![]() .
.
$$$ 108
![]()
À)
![]() ;
;
Â)![]() ;
;
Ñ)
![]() ;
;
D) 0;
Å)![]() .
.
$$$ 109
![]()
![]()
A)
![]() ;
;
B)![]() ;
;
C)
![]() ;
;
D)
![]() ;
;
E)
![]() .
.
$$$ 110
![]() функциясыны»
функциясыны»
![]() кесiндiсiндегi е» ¾лкен м¸нiн табу керек
кесiндiсiндегi е» ¾лкен м¸нiн табу керек
A) 13
B)
![]() ;
;
C) 29;
D)-2;
E) 9 .
$$$ 111
![]() функциясыны»
функциясыны»
![]() кесiндiдегi е» кiшi м¸нiн табу керек.
кесiндiдегi е» кiшi м¸нiн табу керек.
À)7
Â) 21;
Ñ) 0;
D) 14;
Å) –14.
$$$ 112
![]()
À)
![]()
Â)
![]() ;
;
Ñ)
![]() ;
;
D) 2;
Å) 6 .
$$$ 113
![]()
À)
![]() ;
;
Â)
![]() ;
;
Ñ)
![]() ;
;
D)
![]() ;
;
Å)
![]() .
.
$$$ 114
![]() ;
;
À)
![]() ;
;
Â)![]() ;
;
Ñ)![]() ;
;
D)
![]() ;
;
Å)
![]() .
.
$$$ 115
![]()
A)
![]() ;
;
B)![]() ;
;
C)
![]() ;
;
D)
![]() ;
;
E)
![]() .
.
$$$ 116
![]() функциясы
берiлген.
функциясы
берiлген.
![]()
À)![]() ;
;
Â)![]() ;
;
Ñ)![]() ;
;
D)![]() ;
;
Å)![]() .
.
$$$ 117
![]()
![]()
A)
![]() ;
;
B)
![]() ;
;
C)
![]() ;
;
D)
![]() ;
;
E)
![]() .
.
$$$ 118
![]()
![]()
À)
![]() ;
;
B)
![]() ;
;
C)
![]() ;
;
D)
![]() ;
Å)
;
Å)
![]() .
.
$$$119
Егер
![]() функциясы
функциясы
![]() кесіндісінде үзіліссіз болса, онда ол
кесіндісінде үзіліссіз болса, онда ол
![]() кесіндісінде:
кесіндісінде:
A) периодты
B) шенелуі де шенелмеуі де мүмкін
C) шенлмеген
D) шенелген
E) тақ
$$$120
Егер
берілген интервалда
![]() функциясының туындысы
функциясының туындысы
![]() теріс болса, онда
теріс болса, онда
![]() функциясы осы интервалда:
функциясы осы интервалда:
A) нөлге тең
B) өседі
C) тұрақты
D) үзілісті
E) кемиді
2-модуль
$$$121
Интегралды
есептеңіз:
![]() .
.
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$122
Интегралын
есептетеңіз:
![]() .
.
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$123
Егер
![]() функциясы
функциясы
![]() аралығында
дифференциалданса және мына теңдік
орындалса:
аралығында
дифференциалданса және мына теңдік
орындалса:
A)
![]() ,
,
B)
![]()
C)
![]()
D)
![]()
E)
![]()
онда
![]() аралығында
аралығында
![]() функциясының
функциясының
![]() функциясы алғашқы функциясы деп аталады.
функциясы алғашқы функциясы деп аталады.
$$$124
![]()
A) С
B) 1
C) 0
D)
![]()
E)
![]()
$$$125
![]()
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$126
![]()
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$127
Егер
![]() болса,
онда
болса,
онда
![]()
A)

B)

C)
![]()
D)
![]()
E)

$$$128
![]() үшін,
үшін,
![]()
A)
![]()
B)

C)

D)
![]()
E)

$$$129

A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$130
![]()

А)
![]()
B)
![]()
C)
![]()
D)
![]()
E)

$$$131
![]() ,
,![]() дифференциалданатын
функциялары
үшін, бөліктеп интегралдау формуласын
жазу керек:
дифференциалданатын
функциялары
үшін, бөліктеп интегралдау формуласын
жазу керек:
![]()
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$132
 интегралын
есептеуге қажет ауыстыруды көрсетіңіз:
интегралын
есептеуге қажет ауыстыруды көрсетіңіз:
A)
![]()
B)

C)
![]()
D)
![]()
E)
![]()
$$$133
![]() интегралын
есептеуге қажет ауыстыруды көрсетіңіз:
интегралын
есептеуге қажет ауыстыруды көрсетіңіз:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$134
![]()
A)

B)
![]()
C)
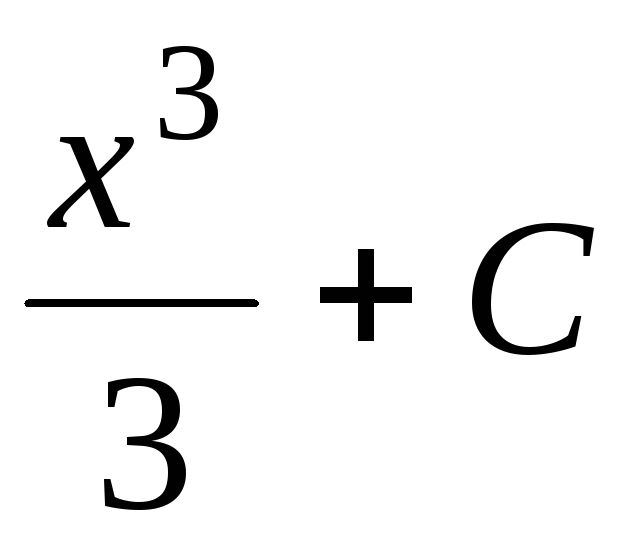
D)

E)

$$$135
![]()
A)
![]()
B)
![]()
C)
![]()
D)

E)
![]()
$$$136
![]()
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$137
![]()
А)
![]()
В)
![]()
С)
![]()
D)
![]()
Е)
![]()
$$$138

А)
![]()
![]()
В)

С)

D)
![]()
Е)

$$$139

А)
![]()
В)
![]()
С)

D)
![]()
Е)
![]()
$$$140
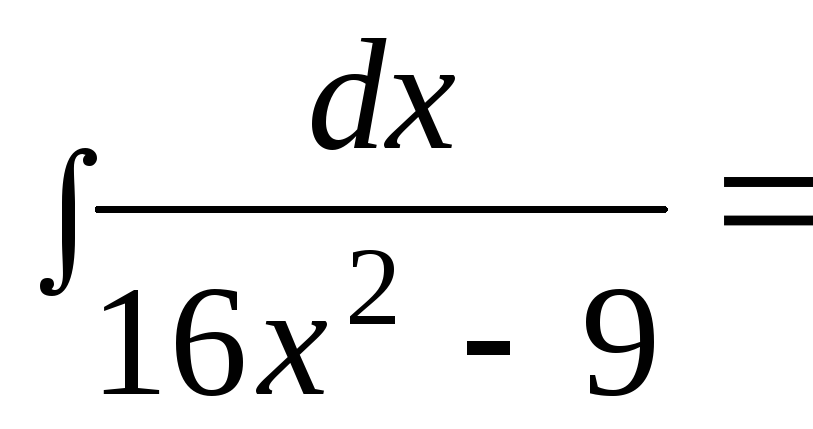
А)
![]()
В)
![]()
С)
![]()
D)
![]()
Е)
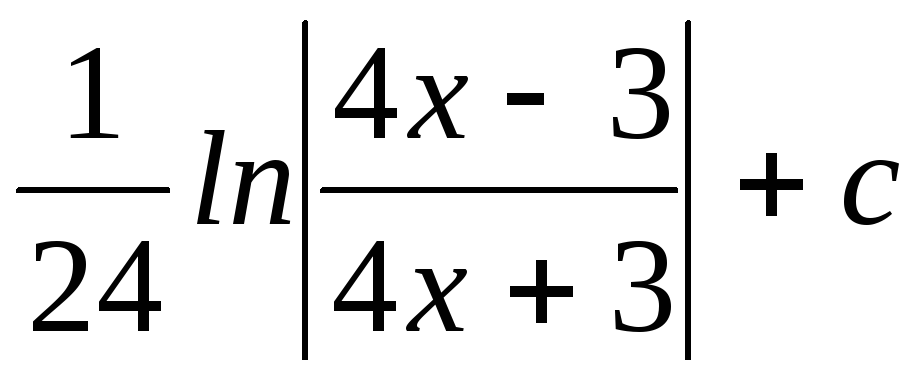
$$$141

А)
![]()
В)
![]()
С)

D)
![]()
Е)
![]()
$$$142
![]()
А)
![]()
В)
![]()
С)
![]()
D)

Е)
![]()
$$$143
![]()
А)
![]()
В)
![]()
С)

D)
![]()
Е)

$$$144
![]()
А)
![]()
![]()
В)

С)

D)

![]()
Е)

![]()
$$$145
![]()
А)
![]()
В)
![]()
С)
![]()
D)
![]()
Е)
![]()
$$$146
![]()
![]() интегралды
есептеңіз:
интегралды
есептеңіз:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$147
![]() функциясының
функциясының
![]() кесіндісіндегі анықталған интегралы
келесі
шек түрінде анықталады:
кесіндісіндегі анықталған интегралы
келесі
шек түрінде анықталады:

A)

B)

C)
![]()
D)

E)
![]()
$$$148
![]() кесіндісіндегі
үзіліссіз функция осы кесіндіде
кесіндісіндегі
үзіліссіз функция осы кесіндіде
A) тұрақты
B) интегралданбайды
C) интегралданады
D) монотонды
E) үзіліссіз емес
$$$149
Берілген кесіндіде функцияның интегралдануының қажетті шартын көрсетіңіз.
A) Осы кесіндіде функция тұрақты болуы керек
B) Осы кесіндіде функция үзіліссіз болуы керек
C) Осы кесіндіде функция нөлге тең болуы керек
D) Осы кесіндіде функция шенелген болуы керек
E) Осы кесіндіде функция кемімелі болуы керек
$$$150
![]() интегралын
есептеңіз:
интегралын
есептеңіз:
A)
![]()
B) 0
C) 1
D) 4
E)
![]()
$$$151
Егер
![]() функциялары
функциялары
![]() аралығында интегралданса және
аралығында интегралданса және
![]() ,
,
![]() теңсіздігі орындалса
,
онда:
теңсіздігі орындалса
,
онда:
A)

B)

C)

D)

E)
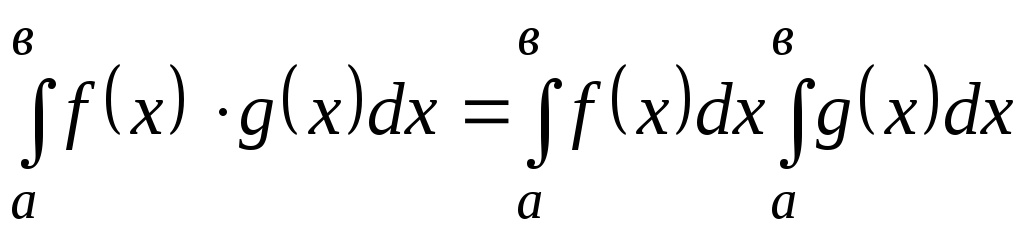
$$$152
Егер
![]() функциясы
функциясы
![]() аралығында үзіліссіз және
аралығында үзіліссіз және
![]() қандайда бір оның алғашқы функциясы
болса , онда
қандайда бір оның алғашқы функциясы
болса , онда

A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$153
Егер
![]() функциясы жұп болса, онда
функциясы жұп болса, онда
A) 1
B) 0
C)

D)

E)
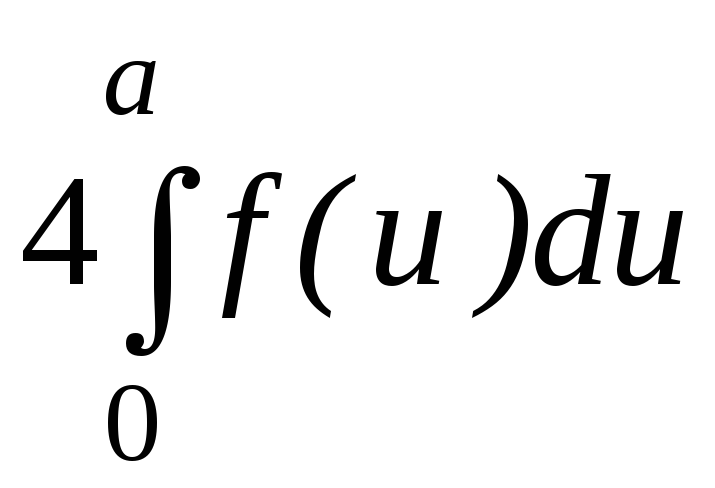
$$$154
Егер
![]() функциясы
тақ болса, онда
функциясы
тақ болса, онда

A)

B)

C) 1
D) 0
E)

$$$155
![]()
А) -0
В) 2
С) -2
D) 1
Е)0
$$$156

А)
![]()
В)
![]()
С) 3
D) 0
Е) 1
$$$157

А) 0
В) 1
С)
![]()
D)
![]()
Е)
![]()
$$$158

А) 3
В) 0
С) 1
D) e+1
Е) e-1
$$$159

А) 2
В) 1
С) -1
D) 0
Е) -2
$$$160
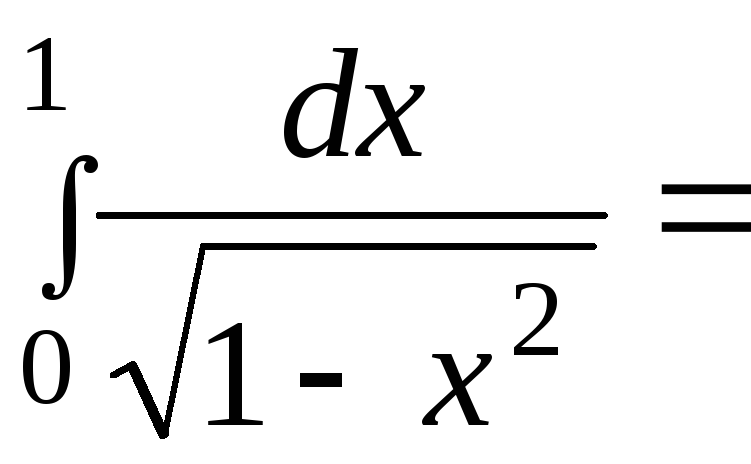
А)
![]()
В)
![]()
С)
![]()
D)
![]()
Е) 0
$$$161
![]()
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$162
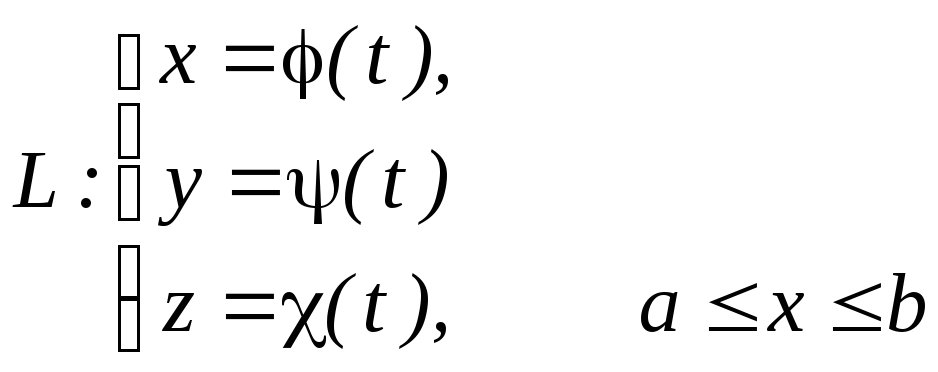 параметірлік
түрде берілген қисықтың ұзындығы
параметірлік
түрде берілген қисықтың ұзындығы
![]()
A)

B)

C)

D)

E)
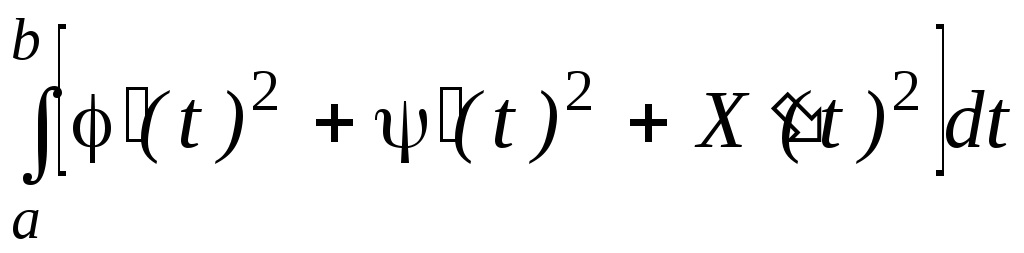
$$$163
Егер
қисық
![]() :
:![]() берілсе, онда
берілсе, онда![]()
A)

B)

C)

D)

E)

$$$164
Егер
қисық полярлық координата түрінде
берілсе
![]() :
:![]() ,
,![]() ,
онда
,
онда![]()
A)

B)

C)

D)

E)

$$$165
Егер
![]() функциясының
функциясының![]() аралығында таңбасын бірнеше рет
өзгертетін болса, онда
аралығында таңбасын бірнеше рет
өзгертетін болса, онда![]() сызықтармен
шенелген жазық фигуранаң ауданын есептеу
формуласын көрсетіңіз
сызықтармен
шенелген жазық фигуранаң ауданын есептеу
формуласын көрсетіңіз
A)

B)

C)
![]()
D)

E)
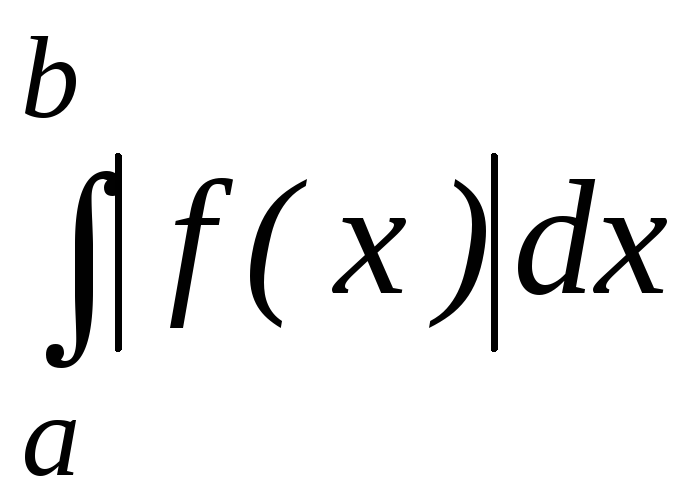
$$$166
![]() қисығының
ұзындығын табыңыз:
қисығының
ұзындығын табыңыз:
A)
![]()
B)-![]()
C)
![]() -1
-1
D)
![]()
E) 1
$$$167
![]() сызықтарымен
шенелген жазық фигураның ауданын
табыңыз:
сызықтарымен
шенелген жазық фигураның ауданын
табыңыз:
A) 1
B) 2
C) 4
D) 8
E) 16
$$$168
![]()
![]() сызықтарымен
шенелген фигураның ауданын табыңыз:
сызықтарымен
шенелген фигураның ауданын табыңыз:
A)
B)
![]()
C)
![]()
D) 3
E) 2
$$$169
Винттік
сызықтың ұзындығын табыңыз:
 .
.
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$170
Бірінші текті меншіксіз интегралдын анықтамасын көрсетіңіз
A)


B)


C)


D)

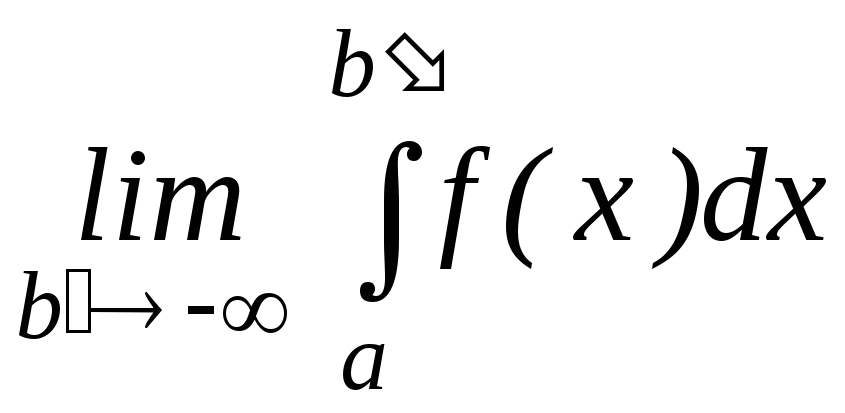
E)

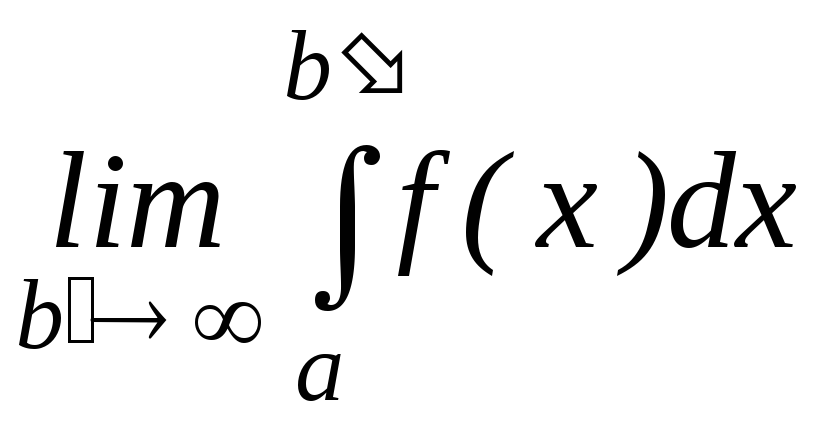
$$$171
 ,
,
 меншіксіз интегралдарының екеуі
бірдей жинақты немесе екеуі бірдей
жинақсыз болуы үшін, келесі шарттың
орындалуы жеткілікті
меншіксіз интегралдарының екеуі
бірдей жинақты немесе екеуі бірдей
жинақсыз болуы үшін, келесі шарттың
орындалуы жеткілікті![]() :
:
A)

![]()
B)
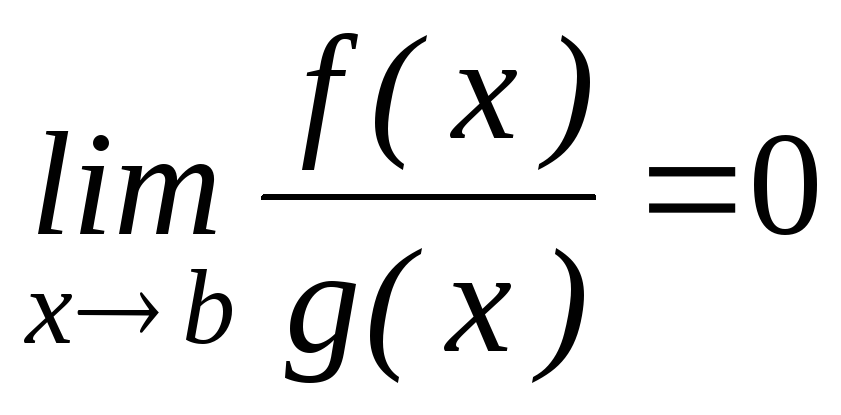
C)

D)
![]()
E)

$$$172
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А)
![]()
В)
![]()
С)
![]()
Д)
![]()
Е) жинақсыз
$$$173
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А)
![]()
В)
![]()
С) 4
Д)
![]()
Е) жинақсыз
$$$174
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А)
![]()
В)
![]()
С)
![]()
Д)
![]()
Е) жинақсыз
$$$175
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А)
![]()
В)
![]()
С)
![]()
Д)
![]()
Е) жинақсыз
$$$176
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А) 3
В) 5
С)
![]()
Д)
![]()
Е) жинақсыз
$$$177
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А) 5
В) жинақсыз
С)
![]()
Д)
![]()
Е) 2
$$$178
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А)
![]()
В) 5
С) жинақсыз
Д)
![]()
Е) 3
$$$179
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А)
![]()
В) 5
С)
![]()
Д) жинақсыз
Е) 3
$$$180
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А) 3
В) 5
С)
![]()
Д)
![]()
Е) жинақсыз
$$$181
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А) жинақсыз
В) 5
С)
![]()
Д)
![]()
Е) 3
$$$182
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А) 2
В)
![]()
С)
![]()
Д)
![]()
Е) жинақсыз
$$$183
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А)
![]()
В) 2
С)
![]()
Д)
![]()
Е) жинақсыз
$$$184
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А)
![]()
В) 2
С)
![]()
Д) 3
Е) жинақсыз
$$$185
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А) жинақсыз
В) 4
С) 3
Д) 2
Е)
![]()
$$$186
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А) жинақсыз
В) 5
С)
![]()
Д)
![]()
Е) 3
$$$187
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А) 5
В) жинақсыз
С)
![]()
Д)
![]()
Е) 3
$$$188
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А) 3
В) 4
С)
![]()
Д) 2
Е) жинақсыз
$$$189
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А) 2
В) 4
С) 3
Д)
![]()
Е) жинақсыз
$$$190
Меншіксіз
интеграл жинақты болса, оны есептеу
керек:
![]()
А) жинақсыз
В) 4
С) 3
Д) 2
Е)
![]()
3-модуль
$$$191
![]() функциясының
функциясының
![]() нүктесіндегі x
бойынша дербес өсімшесін
көрсетіңіз
нүктесіндегі x
бойынша дербес өсімшесін
көрсетіңіз
А)
![]()
В)
![]()
С)
![]()
Д)
![]()
Е)
![]()
$$$192
![]() функциясының
функциясының
![]() нүктесіндегі y
бойынша
дербес өсімшесін көрсетіңіз
нүктесіндегі y
бойынша
дербес өсімшесін көрсетіңіз
А)
![]()
В)
![]()
С)
![]()
Д)
![]()
Е)
![]()
$$$193
![]() функциясының
функциясының
![]() нүктесіндегі
толық өсімшесін
көрсетіңіз
нүктесіндегі
толық өсімшесін
көрсетіңіз
А)
![]()
В)
![]()
С)
![]()
Д)
![]()
Е)
![]()
$$$194
![]() функциясының
функциясының
![]() айнымал бойынша дербес туындысы:
айнымал бойынша дербес туындысы:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$195
![]() функциясының
y
айнымал бойынша дербес туындысы:
функциясының
y
айнымал бойынша дербес туындысы:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$196
![]() функциясының
функциясының
![]() нүктесіндегі
дифференциалын көрсетіңіз
нүктесіндегі
дифференциалын көрсетіңіз
А)
![]()
В)
![]()
С)
![]()
Д)
![]()
Е)
![]()
$$$197
![]() функциясының
функциясының
![]() нүктесіндегі екінші
ретті дифференциалын көрсетіңіз
нүктесіндегі екінші
ретті дифференциалын көрсетіңіз
А)
![]()
В)
![]()
С)
![]()
Д)
![]()
Е)
![]()
$$$198
Егер
![]() функциясының
функциясының![]() -
стационар нүктесінде
-
стационар нүктесінде![]()
![]() ,
,![]() болып,
болып,![]() ,
,![]() шарты орындалса , онда
шарты орындалса , онда![]() нүктесінде функциясының
нүктесінде функциясының
А) минимум болады
В) экстремумі жоқ
C) минимумы болмайды
D) максимумы болады
E) ең үлкен мәні болады.
$$$199
Егер
![]() функциясының
функциясының
![]() -
стационар нүктесінде
-
стационар нүктесінде
![]()
![]() ,
,
![]() болып,
болып,
![]() ,
,
![]() шарты орындалса , онда
шарты орындалса , онда
![]() нүктесінде функциясының
нүктесінде функциясының
А) максимумы болады
В) экстремумі жоқ
C) минимумы болмайды
D) локальді минимумі болады
E) ең үлкен мәні болады.
$$$200
Егер
![]() функциясының
функциясының
![]() -
стационар нүктесінде
-
стационар нүктесінде
![]()
![]() ,
,
![]() болып,
болып,
![]() ,
,
![]() шарты орындалса , онда
шарты орындалса , онда
![]() нүктесінде функциясының
нүктесінде функциясының
А) ең үлкен мәні болады
В) экстремумі жоқ
C) минимумы болмайды
D) локальді минимумі болады
E) локальді максимумы болады .
$$$201
![]() функциясының
толық дифференциалын табыңыз:
функциясының
толық дифференциалын табыңыз:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$202
Егер
![]() болса, онда
болса, онда
![]() табыңыз:
табыңыз:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$203
Егер
![]() болса, онда
болса, онда
![]() :
:
A)
![]()
В)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$204
Егер
![]() болса, онда
болса, онда
![]() :
:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$205
Егер
![]() болса, онда
болса, онда![]() :
:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$206
![]() функцияның
толық дифференциалын:
функцияның
толық дифференциалын:
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
$$$207
Егер
![]() .болса,
онда
.болса,
онда
![]()
A)
![]()
B)
![]()
C)
![]()
D)
![]()
E)
![]()
