
шпор по вышмат 2семестр
.docА
$$$
1![]() мен
мен
![]() жиындарының бірігуін көрсетіңіз
C={x: x
жиындарының бірігуін көрсетіңіз
C={x: x![]() A
немесе x
A
немесе x![]() B}
B}
$$$
2![]() мен
мен
![]() жиындарының қиылысуын көрсетіңіз
C={x:
x
жиындарының қиылысуын көрсетіңіз
C={x:
x![]() A
және x
A
және x![]() B}
B}
$$$
3![]() мен
мен
![]() жиындарының айырымын көрсетіңіз
C={x: x
жиындарының айырымын көрсетіңіз
C={x: x![]() A
және x
A
және x![]() B}
B}
$$$
8 A={2, -3, 0, a, б, в} мен B={-1, 0, 4, в} жиындарының
бірігуін көрсетіңіз.
![]()
C)
{2, -3, 0, а, б, в, -1, 4}
$$$ 9 A={2, -3, 0, a, б, в} мен B={-1, 0, 4, в} ж-ң
қиылысуын көрсетіңіз.
![]() D)
{0, в}
$$$10 A={2, -3, 0, a, б, в} мен B={-1, 0, 4, в} ж-ң
айырымын көрсетіңіз.
D)
{0, в}
$$$10 A={2, -3, 0, a, б, в} мен B={-1, 0, 4, в} ж-ң
айырымын көрсетіңіз.
![]() E)
{2, -3, а, б}
E)
{2, -3, а, б}
$$$
11
![]() нақты санының
маңайын көрсетіңіз (
>0): A)
{x
нақты санының
маңайын көрсетіңіз (
>0): A)
{x![]() R:
a-
< x < a+}
$$$
12
R:
a-
< x < a+}
$$$
12
![]() нақты с-ң оң жақ
маңайын көрсетіңіз (
>0): B)
{x
нақты с-ң оң жақ
маңайын көрсетіңіз (
>0): B)
{x![]() R:
a ≤ x < a+}
$$13
R:
a ≤ x < a+}
$$13
![]() нақты санының сол жақ
маң-н көрсетіңіз (
>0): C)
{x
нақты санының сол жақ
маң-н көрсетіңіз (
>0): C)
{x![]() R:
a-
< x ≤ a}
$$$ 14 a= +∞ (плюс ақырсыздық) нүктесінің
маңайын көрсетіңіз (
>0): D)
(,
+∞]
$$$ 15 a= -∞ (минус ақырсыздық) нүктесінің
маңайын көрсетіңіз (
>0): E)
[-∞; -)
R:
a-
< x ≤ a}
$$$ 14 a= +∞ (плюс ақырсыздық) нүктесінің
маңайын көрсетіңіз (
>0): D)
(,
+∞]
$$$ 15 a= -∞ (минус ақырсыздық) нүктесінің
маңайын көрсетіңіз (
>0): E)
[-∞; -)
$$$
16 a= ∞ (ақырсыздық) нүктесінің
маңайын көрсетіңіз (
>0): A)
[-∞; -)
![]() (;
+∞]
(;
+∞]
$$$128
![]() үшін,
үшін,
![]()
E)
![]()
$$$ 208 Айнымалдары ажыратылған бірінші ретті дифференциалдық теңдеуді көрсетіңіз
C)
![]()
$$$ 209 Айнымалдары ажыратылатын бірінші ретті дифференциалдық теңдеуді көрсетіңіз
D)
![]()
Б
$$$149 Берілген кесіндіде функцияның интегралдануының қажетті шартын көрсетіңіз.
D) Осы кесіндіде функция шенелген болуы керек
$$$170
Бірінші текті меншіксіз интегралдын анықтамасын көрсетіңіз
Е)
![]()
![]()
$$$&&
Біртекті
бірінші ретті дифференциалдық теңдеуді
көрсетіңіз
E)
![]()
$$$ 213 Бернулли теңдеуін (дифференциалдық) көрсетіңіз
С)![]()
$$$ 214 Біртекті бірінші ретті дифференциалдық теңдеуді айнымалдары ажыратылатын теңдеуге келтіретін айнымал ауыстыруын көрсетіңіз
D)
![]()
$$$
216 Бернулли теңдеуін шешуге арналған
айнымал ауыстыруын көрсетіңіз A)
![]()
$$$ 217 Бернулли теңдеуін сызықтық теңдеуге келтіретін айнымал ауыстыруын көрсетіңіз
B)
![]()
В
$$$169
Винттік
сызықтың ұзындығын табыңыз:
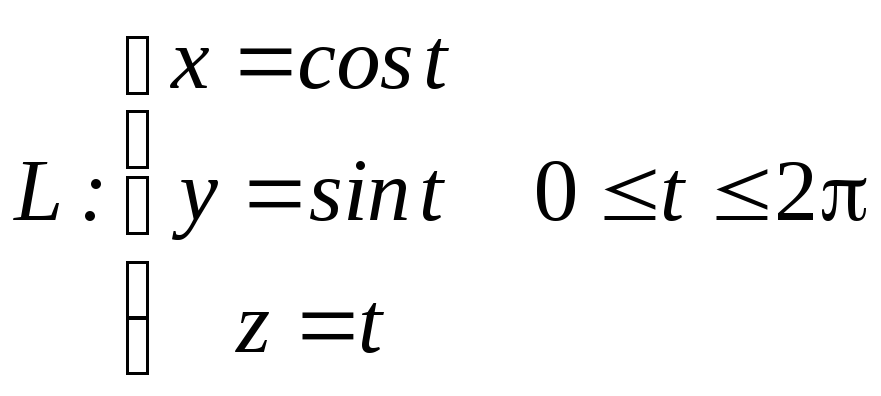 .
D)
.
D)
![]()
Д
$$$236 Дифференциалдық теңдеудің реті деп:
A) теңдеудегі туындының жоғарғы ретін
$$$245
Дифференциалдық
теңдеуді шешіңіз:
![]() . E)
. E)
![]()
$$$246
Дифференциалдық
теңдеуді шешіңіз:
![]() . А)
. А)
![]()
$$$247
Дифференциалдық
теңдеуді шешіңіз:
![]() . В)
. В)
![]()
$$$248
Дифференциалдық
теңдеуді шешіңіз:
![]() С)
С)
![]()
$$$249
Дифференциалдық
теңдеуді шешіңіз:
![]() . D)
. D)
![]()
Е
$$$
4Егер U-негізгі жиын,
![]() болса, онда
болса, онда
D)
![]() $$$ 5Егер U-негізгі жиын,
$$$ 5Егер U-негізгі жиын,
![]() болса, онда
болса, онда
E)
![]()
$$$
6Егер U-негізгі жиын,
![]() болса, онда
болса, онда
A)
![]() $$$
7Егер U-негізгі жиын,
$$$
7Егер U-негізгі жиын,
![]() болса, ондаB)
болса, ондаB)
![]()
$$$
17Егер X-жоғарыдан шенелген жиын, ал M
оның жоғарғы шекарасы болса, онда B)
![]() $$$ 18Егер X-төменнен шенелген жиын,
ал m оның төменгі шекарасы болса, онда
C)
$$$ 18Егер X-төменнен шенелген жиын,
ал m оның төменгі шекарасы болса, онда
C)
![]() $$$ 19Егер X-шенелген жиын болса, онда
$$$ 19Егер X-шенелген жиын болса, онда
![]()
D)
![]()
$$$
20Егер M саны X-cандар жиынының ең үлкен
элементі болса, онда Е)
![]()
$$$
21Егер m саны X-cандар жиынының ең кіші
элементі болса, онда A)
![]()
$$$
25 Егер X=[1;2)
болса, онда
![]() табыңыз
Е)
табыңыз
Е)
![]() жоқ
жоқ
$$$
26 Егер X=(2;3]
болса, онда
![]() A)
2
$$$
27 Егер X=(2;3) болса, онда
A)
2
$$$
27 Егер X=(2;3) болса, онда
![]() және
және
![]() табыңыз
B)
табыңыз
B)
![]() -жоқ;
-жоқ;
![]() 2
$$$
28 Егер X=(2;3]
болса, онда
C)
maxX=supX=3
2
$$$
28 Егер X=(2;3]
болса, онда
C)
maxX=supX=3
$$$
29 Егер y=f(x) функциясы D аймағында (қатаң)
өспелі болса, онда D)
![]()
$$$
30 Егер y=f(x) функциясы D аймағында (қатаң)
кем-і болса, онда E)
![]()
$$$
31 Егер y=f(x) функциясы D аймағында кем-н
болса, онда
A)
![]()
$$$
32 Егер y=f(x) функциясы D аймағында өспейтін
болса, онда B)
![]()
$$$
33 Егер |q|<1 болса, онда
![]() C)
0
C)
0
$$$
34 Егер |q|>1 болса, онда
![]() D)
∞
D)
∞
$$$
24 Егер X=[1;2)
болса, онда
![]() D)
2
D)
2
$$$
36 Егер
![]() және
және
![]() болса, онда
болса, онда
![]() A)
2
A)
2
$$$
44 Егер
![]() тең болса, онда
тең болса, онда
D)
![]() ïåí
ïåí
![]() функциялары,
функциялары,
![]() ұмтылғанда, эквивалентті;
ұмтылғанда, эквивалентті;
$$$
45 Егер
![]() болса, онда
болса, онда
Å)
![]()
![]() ;
;
$$$46
Егер
![]() ,
,
![]() -ақырлы
сан болса, онда:
A)
-ақырлы
сан болса, онда:
A)![]() -нүктесінің
қандайда бір манайында
-нүктесінің
қандайда бір манайында
![]() шенелген функция
шенелген функция
$$$47
Егер
![]() біржақты шектері бар, бірақ
біржақты шектері бар, бірақ
![]() теңдіктерінің ең болмағанда біреуі
орындалмаса, онда
теңдіктерінің ең болмағанда біреуі
орындалмаса, онда
![]() функциясы
функциясы
![]() нүктесінде
B)
1 текті үзілісті деп
аталады.
нүктесінде
B)
1 текті үзілісті деп
аталады.
$$$48
Егер
![]() -тізбегі
шенелген, ал
-тізбегі
шенелген, ал
![]() -ақырсыз
үлкен тізбек болса, онда: C)
-ақырсыз
үлкен тізбек болса, онда: C)
![]()
$$$50
Егер
E)
![]()
теңдігі
орындалса, онда
![]() функциясы
функциясы
![]() нүктесінде
үзіліссіз деп аталады
нүктесінде
үзіліссіз деп аталады
$$$51
Егер
![]() нүктесіндегі
нүктесіндегі
![]() функциясының біржақты шектерінің ең
болмағанда біреуі жоқ немесе ақырсыз
болса, онда
функциясының біржақты шектерінің ең
болмағанда біреуі жоқ немесе ақырсыз
болса, онда
![]() нүктесінде
нүктесінде
![]() функциясы
функциясы
A) екінші текті үзілісті деп аталады
$$$52
Егер
![]() және
және
![]() үшін
үшін
![]() болса, онда: B)
болса, онда: B)
![]()
$$$56
Егер
![]() -сандық
тізбек жинақты болса, к4 ол:
A)
шенелген
-сандық
тізбек жинақты болса, к4 ол:
A)
шенелген
$$$119
Егер
![]() функциясы
функциясы
![]() кесіндісінде үзіліссіз болса, онда ол
кесіндісінде үзіліссіз болса, онда ол
![]() кесіндісінде:
E)
шенелген
кесіндісінде:
E)
шенелген
$$$120
Егер
берілген интервалда
![]() фун-ң туындысы
фун-ң туындысы
![]() теріс болса, онда
теріс болса, онда
![]() функциясы осы интервалда: E)
кемиді
функциясы осы интервалда: E)
кемиді
$$$123
Егер
![]() функциясы
функциясы
![]() аралығында
дифференциалданса және мына теңдік
орындалса:
аралығында
дифференциалданса және мына теңдік
орындалса:
E)
![]()
онда
![]() аралығында
аралығында
![]() функциясының
функциясының
![]() функциясы алғашқы функциясы деп аталады.
функциясы алғашқы функциясы деп аталады.
$$$127
Егер
![]() болса, онда
болса, онда
![]()
E)
![]()
$$$151
Егер
![]() функциялары
функциялары
![]() аралығында интегралданса және
аралығында интегралданса және
![]() ,
,
![]() теңсіздігі орындалса
,
онда:
теңсіздігі орындалса
,
онда:
А)![]()
$$$152
Егер
![]() функциясы
функциясы
![]() аралығында үзіліссіз және
аралығында үзіліссіз және
![]() қандайда бір оның алғашқы функциясы
болса , онда
қандайда бір оның алғашқы функциясы
болса , онда
![]()
В)
![]()
$$$153
Егер
![]() функциясы жұп болса, онда
функциясы жұп болса, онда
![]() C)
C)
![]()
$$$154
Егер
![]() функциясы
тақ болса, онда
функциясы
тақ болса, онда
![]() В)
0
В)
0
$$$163
Егер
қисық
![]() :
:
![]() берілсе, онда
берілсе, онда
![]()
С)
![]()
$$$164
Егер қисық полярлық координата түрінде
берілсе
![]() :
:
![]() ,
,
![]() ,
онда
,
онда
![]() В)
В)
![]()
$$$165
Егер
![]() функциясының
функциясының
![]() аралығында таңбасын бірнеше рет
өзгертетін болса, онда
аралығында таңбасын бірнеше рет
өзгертетін болса, онда
![]() сызықтармен
шенелген жазық фигуранаң ауданын есептеу
формуласын көрсетіңіз
Е)
сызықтармен
шенелген жазық фигуранаң ауданын есептеу
формуласын көрсетіңіз
Е)
![]()
$$$198
Егер
![]() функциясының
функциясының
![]() -
стационар нүктесінде
-
стационар нүктесінде
![]()
![]() ,
,
![]() болып,
болып,
![]() ,
,
![]() шарты орындалса , онда
шарты орындалса , онда
![]() нүктесінде функциясының
C)
минимумы болмайды
нүктесінде функциясының
C)
минимумы болмайды
$$$199
Егер
![]() функциясының
функциясының
![]() -
стационар нүктесінде
-
стационар нүктесінде
![]()
![]() ,
,
![]() болып,
болып,
![]() ,
,
![]() шарты орындалса , онда
шарты орындалса , онда
![]() нүктесінде функциясының D)
локальді минимумі болады
нүктесінде функциясының D)
локальді минимумі болады
$$$200
Егер
![]() функциясының
функциясының
![]() -
стационар нүктесінде
-
стационар нүктесінде
![]()
![]() ,
,
![]() болып,
болып,
![]() ,
,
![]() шарты орындалса , онда
шарты орындалса , онда
![]() нүктесінде функциясының Е)локальді
максимумы болады
нүктесінде функциясының Е)локальді
максимумы болады
$$$202
Егер
![]() болса, онда
болса, онда
![]() табыңыз:
В)
табыңыз:
В)
![]()
$$$203
Егер
![]() болса, онда
болса, онда
![]() :
С)
:
С)
![]()
$$$204Егер
![]() болса, онда
болса, онда
![]() :
D)
:
D)
![]()
$$$205
Егер
![]() болса, онда
болса, онда
![]() 亢:
Е)
亢:
Е)
![]()
$$$206
![]() функцияның толық дифференциалын:
А)
функцияның толық дифференциалын:
А)![]()
$$$207
Егер
![]() .болса,
онда
.болса,
онда
![]() В)
В)![]()
$$$
223 Егер
![]() - n-
ші
ретті дифференциалдық оператор болса,
онда оның біртектілік
қасиетін
көрсетіңіз
- n-
ші
ретті дифференциалдық оператор болса,
онда оның біртектілік
қасиетін
көрсетіңіз
С)
![]() ,
С-сан
,
С-сан
$$$
224Егер
![]() - n-
ші
ретті дифференциалдық оператор болса,
онда оның аддитивтік
қасиетін
көрсетіңіз
- n-
ші
ретті дифференциалдық оператор болса,
онда оның аддитивтік
қасиетін
көрсетіңіз
D)
![]()
$$$
227 Егер
![]() интервлында
интервлында
![]() -ші
ретке дейінгі туындылары бар
-ші
ретке дейінгі туындылары бар
![]() функциялары осы интервалда сызықты
тәуелді болса, онда
функциялары осы интервалда сызықты
тәуелді болса, онда
B)
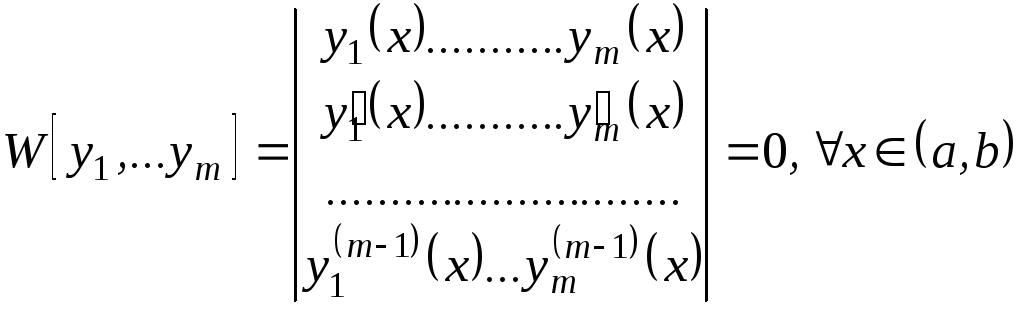
$$$
232 Егер коэффициенттері тұрақты сызықтық
біртекті
![]() -ші
ретті
-ші
ретті
![]() дифференциалдық теңдеудің сипаттаушы
теңдеуінің түбірлері:
дифференциалдық теңдеудің сипаттаушы
теңдеуінің түбірлері:
![]() әртүрлі, өзара тең емес сандар болса,
онда
әртүрлі, өзара тең емес сандар болса,
онда
![]() дифференциалдық теңдеудің фундаментальды
ше-р жүйесін көрсетіңіз
дифференциалдық теңдеудің фундаментальды
ше-р жүйесін көрсетіңіз
В)
![]()
$$$ 287 Егер
![]() екі
еселі интегралдағы айн-ы
екі
еселі интегралдағы айн-ы
![]() ,
,
![]() ,
арқылы ауыстырса, онда Якобиан:
В)
,
арқылы ауыстырса, онда Якобиан:
В)
![]() тең
болады
тең
болады
$$$288 Егер
![]() (мұндағы
(мұндағы
![]() және
және
![]() шекаралық нүктелерінде ғана қиылысатын
аймақтар) болса, онда
шекаралық нүктелерінде ғана қиылысатын
аймақтар) болса, онда
![]()
C)
![]()
$$$ 301
Егер
![]() және
және
![]() пластинка бетінің ты-ы болса, онда
пластинка бетінің ты-ы болса, онда
![]() интегралы нені өрнектейді? А)
пластинканың
массасын;
интегралы нені өрнектейді? А)
пластинканың
массасын;
$$$ 302
Егер
G аймағы
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]() ,
,
![]() сызықтарымен шенелген болса (
сызықтарымен шенелген болса (![]() функциялары
функциялары
![]() кесіндісінде үзіліссіз), онда
кесіндісінде үзіліссіз), онда
![]()
B)
![]()
$$
303 Егер G аймағы
![]()
![]() сызықтарымен шенелген болса, онда
сызықтарымен шенелген болса, онда![]() және
және
![]() функциялары
функциялары
![]() кесіндісінде үзіліссіз)
кесіндісінде үзіліссіз)
![]()
C)
![]()
$$$
331 Егер
![]() ,
,
![]() ,
,
![]() болса, онда
болса, онда
![]() интегралды есептеңіз А)
интегралды есептеңіз А)
![]()
$$$
333 Егер
![]() ,
,
![]() ,
,
![]() болса, онда
болса, онда
![]() интегралын есептеңіз C)
1
интегралын есептеңіз C)
1
$$$
335 Егер
![]() ,
,
![]() ,
,
![]() болса, онда
болса, онда
![]() интегралын есептеңіз Е)
3
интегралын есептеңіз Е)
3
И
$$$121
Интегралды
есептеңіз:
![]() .
.
E)
![]()
$$$122
Интегралын есептетеңіз:
![]() .
.
E)
![]()
$$$
88
Кез-келген
![]() ñàíû ¾øií
ñàíû ¾øií
![]()
Ñ)
![]() ;
;
$$$
228
Кез
келген аралықта сызықты
тәуелсіз функциялар жүйесін
көрсетіңізС)
![]() ,
,
![]() - өзара тең емес әртүрлі сандар
- өзара тең емес әртүрлі сандар
![]()
$$$
229 Кез келген аралықта сызықты
тәуелсіз фун-р жүйесін
көрсетіңіз D)
![]()
$$$
230 Кез келген аралықта сызықты
тәуелсіз фун-р жүйесін
көрсетіңіз Е)
![]()
$$$
231 Коэффициенттері тұрақты сызықтық
біртекті
![]() -ші
ретті
-ші
ретті
![]() ,
,
![]() дифференциалдық теңдеудің фундаментальды
(іргелі) шешімдер жүйесі қандай шарттарды
қанағаттандырады?
дифференциалдық теңдеудің фундаментальды
(іргелі) шешімдер жүйесі қандай шарттарды
қанағаттандырады?
А)
![]() -
функциялары
-
функциялары
![]() аралығында сызықты тәуелсіз
және
олардың әрқайсысы көрсетілген біртекті
теңдеудің шешімдері
аралығында сызықты тәуелсіз
және
олардың әрқайсысы көрсетілген біртекті
теңдеудің шешімдері
$$$
233 Коэффициенттері тұрақты сызықтық
біртекті
![]() -ші
ретті
-ші
ретті
![]() ,
,
![]() дифференциалдық теңдеудің жалпы шешімін
көрсетіңіз
дифференциалдық теңдеудің жалпы шешімін
көрсетіңіз
С)
![]() ,
,
![]() -
функциялары
-
функциялары
![]() аралығында көрсетілген біртекті
теңдеудің фундаментальды шешімдер
жүйесі
аралығында көрсетілген біртекті
теңдеудің фундаментальды шешімдер
жүйесі
$$$
234 Коэффициенттері тұрақты сызықтық
біртекті емес
![]() -ші
ретті
-ші
ретті
![]() ,
,
![]() дифференциалдық теңдеудің жалпы шешімін
көрсетіңіз
дифференциалдық теңдеудің жалпы шешімін
көрсетіңіз
Д)
![]() ,
,
![]()
![]() -
берілген диф. теңдеудің қандай да бір
дербес шешімі;
-
берілген диф. теңдеудің қандай да бір
дербес шешімі;
![]() -
біртекті диф. теңдеудің жалпы шешімі
-
біртекті диф. теңдеудің жалпы шешімі
