Технология построения трендов в Microsoft Excel Порядок выполнения лабораторной работы

1. Построите XY-диаграмму исходного динамического ряда.

2. Создайте копию диаграммы исходного ряда (не обязательно).

3. Выделите ряд данных, для которого следует построить или добавить тренд.

4. В меню "Вставка" выберите опцию Добавить линию тренда (Insert Trendline).

В открывшемся диалоговом окне "Тип" выберите нужный тип регрессионного анализа линии тренда. Окно "Линия тренда" (Trendline) предоставляет возможность моделировать тренд, используя пять основных типов регрессии:Linear - линейную, Logaritmic - логарифмическую, Polinomial - полиномиальную (степени от двух до шести задаются в прокурчиваемом списке Степень), Power - степенную, Exponential - экспоненциальную.

2. В том же окне выбрать вкладку "Параметры".

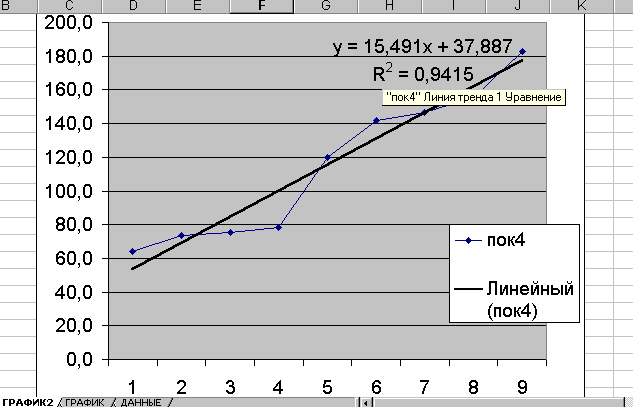
3. В открывшемся диалоговом окне параметров тренда установите флажок "Показывать уравнение на диаграмме" и флажок "Поместить на диаграмму величину достоверности аппроксимации R^2".

По желанию устанавливается необходимое число периодов для изображения возможного прогноза вперед или назад, а также вводится название моделируемого тренда, которое будет помещено в метку диаграммы. Названия даются и по умолчанию, но без указания степени полиномиального тренда.

7. Если не нужен свободный член уравнения, следует активизировать флажок "Пересечение кривой с осью Y в точке 0".

8. Активизируйте кнопку "ОК".

9. Для получения каждого нового тренда повторить шаги от п. 2 до п. 7.

Форматирование линии тренда

Активизируйте диаграмму.

• Сделайте двойной щелчок по линии тренда.

• Выберите вкладку «Вид».

• В группе «Линия» укажите стиль, цвет, толщину линий.

• Проверьте образец отформатированной линии тренда в диалоговом окне .

Форматирование метки линии тренда.

• Активизируйте диаграмму.

• Сделайте двойной щелчок по линии тренда.

• Выберите вкладку «Число».

• «Выберите нужный числовой формат».

Пример построения линии тренда.

КОРРЕЛЯЦИЯ

В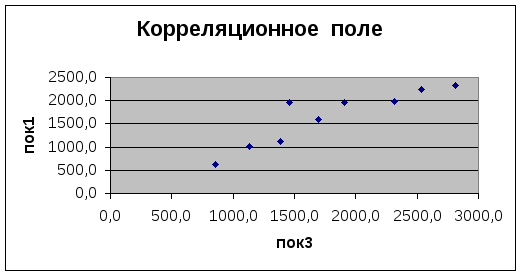данном разделе работы следует построить корреляционную матрицу, отражающую линейную связь между всеми рядами показателей. Необходимо использовать вышеприведенные ис ходные данные и использовать пакет анализа данныхExcel. Необходимо также вывести корреляционные поля, позволяющие визуально оценить корреляционные связи.

Задание на выполнение лабораторной работы:

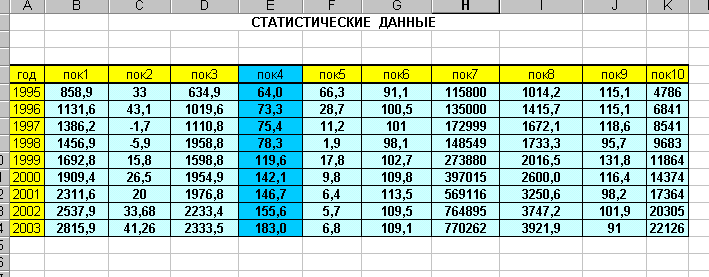
1. Выберите любые 5 рядов данных для упражнения.Используя табличный процессор, попытайтесь найти истинную форму тренда показателя за весь временной промежуток и оцените качество построенного тренда. Сделайте прогноз: по найденному тренду на 2-3 периода.

2. Выберите показатели для упражнения (не менее 5 пар).

а) Постройте корреляцинныю таблицу.

в) Для выбранных данных постройте корреляционные поля.

с) Сделайте качественные выводы о тесноте линейной связи отдельных показателей.

Контрольные вопросы:

1. Какова методика поиска тренда в MS Excel?

2. На основании какого показателя можно выбирать лучший тренд в MS Excel?

3. Какова методика оценки корреляционной завасимости данных в MS Excel?

Литература: 1ocн[178-196], 6ocн[17-21], 2[43-53],4доп[114-134].

Лабораторная работа 5.

Тема: Регрессионный анализ.

Связи между различными величинами носят функциональный или корреляционный характер. Функциональная зависи­мость означает детерминированную, предопределенную заранее связь между величинами и может быть выражена точным мате­матическим соотношением. Корреляционная зависимость означает стохастическую (случайную) связь между величинами и общем случае выражается ковариацией или коэффициентом корреляции, при этом одна независимая случайная величина рассматривается как фактор, а другая случайная величина - как основной признак, для которого оценивается мера тесноты связи с фактором.

Форма взаимосвязи случайных величин и функции получила название уравнения регрессии. Различают простую (парную) и множественную регрессию линейного и криволинейного (квадратичного, экспоненциального, полулогарифмического и т.д.) типа. Вид и параметры уравнения регрессии устанавливаются с помощью метода наименьших квадратов отклонений эмпирических данные от выровненных.

Статистическая оценка тесноты связи основана на показа­телях вариации:

• общая дисперсия результативного признака, обусловлен­ная влиянием всех факторов в совокупности -;

• факторная дисперсия результативного признака, отражающая вариацию результативного признака от воздействия фактора -;

• остаточная дисперсия результативного признака, отража­ющая вариацию результативного признака от воздействия всех прочих факторов, кроме выделенного-.

Основное соотношение: .

Качественная оценка степени связи случайных переменных - коэффициент детерминации, который вычисляется как отношение факторной к общей дисперсии - R², доля факторной дисперсии в общей дисперсии. Иногда используется индекс корреляции - R. Для оценки значимости R применяется F-критерий Фишера. Фактическая величина критерия сравнивается с критическим значением, определяемым с учетом уровня значимости и числа сте­пеней свободы. Если фактическое значение больше критического, величина R признается существенной.

При значениях коэффициента детерминации более 0,7 вариа­ции зависимой переменной, в основном, обусловлены влиянием факторов, и регрессионные модели признаются пригодными для их прак­тического использования в целях прогнозирования.

Найденные коэффициенты уравнения регрессии являются оцен­ками истинных значений параметров. Если анализируется совокуп­ность малого размера (до 30 значений), то для определения довери­тельного интервала параметров используют распределение Стьюдента (значение t-критерия Стьюдента). Рассчитанные значения t-критериев сравниваются с критическими с учетом принятого уровня значимости и числа степеней свободы и признаются типичными, если фактическое значение больше критического.

Если анализируется совокупность достаточно большого размера, вместо таблицы распределения Стьюдента пользуются таблицей интеграла вероятностей Лапласа.

Как выполнять в MS Excel.

Для получения коэффициентов регрессии используется процедура "Регрессия" пакета анализа. Кроме того, могут быть использованы функция "ЛИНЕЙН" для получения параметров регрессионного уравнения и функция "ТЕНДЕНЦИЯ" для получения предсказанных значений Y в требуемых точках.

Для реализации процедуры Регрессия необходимо: выполнить команду "Сервис" ->"Анализ данных", в появившемся диалоговом окне "Анализ данных" в списке "Инструменты анализа" выбрать строку "Регрессия". В появившемся диалоговом окне задать "Входной интервал Y", то есть ввести ссылку на диапазон анализируемых зависимых данных, содержащий один из столбцов данных. Указать "Входной интервал X", то есть ввести ссылку на диапазон независимых данных. Указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Размер выходного диапазона будет определен автоматически. Если небходимо визуально проверить отличие экспериментальных точек от предсказанных по регрессионной модели, следует установить флажок в поле График подбора, нажать кнопку ОК.

Результаты анализа. Выходной диапазон будет включать в себя результаты дисперсионного анализа, коэффициенты регрессии, стандартную погрешность вычисления Y, среднеквадратичные отклонения, число наблюдений, стандартные погрешности для коэффициентов.

Приводимое значение R-квадрат (коэффициент детерминации) определяет, с какой степенью точности полученное регрессионное уравнение аппроксимируется исходные данные.

Задание: Построить и объяснить регрессионную модель для предсказания изменений уровня заболеваемости органов дыхания (Y) в зависимости от содержания в воздухе двуокиси углерода (X1) и степени запыленности (X2). В таблице приведены данные наблюдений в течение 29 месяцев.

X1	X2	Y
1	1,3	1160
1	1,3	1155
1,1	1,4	1158
1,1	1,4	1157
1,1	1,5	1160
1,1	1,5	1161
1	1,4	1157
1	1,5	1159
1,2	1,6	1256
1,2	1,7	1260
0,6	1	1040
0,6	1	1039
0,7	1,1	1039
0,7	1,15	1040
0,75	1,2	1040
0,7	1,2	1039
0,7	1,3	1040
0,7	1,3	1039
0,8	1,4	1140
0,8	1,4	1138
0,78	1,5	1240
0,8	1,5	1239
0,78	1,5	1241
0,78	1,6	1240
0,8	1,7	1239
0,8	1,8	1239
0,75	1,8	1240
0,78	1,9	1238
0,75	1,9	1238

Сверьте решение :Y=682+91*X1+275*X2.

Контрольные вопросы:

1. Какова методика получения регрессионных уравнений в MS Excel?

2. Какие показатели характеризуют качество регрессионных уравнений в MS Excel?

3. Как визуально можно проверить отличие экспериментальных точек от предсказанных по регрессионной модели в MS Excel?

Литература: 1осн. [273-285], 2осн. [42-74], 6осн. [22-30], 2доп. [60-76], 3доп. [260-266], 4 доп. [135-142], 6доп. [206-214].

Лабораторная работа 6.

Тема: Анализ временных рядов. Коинтеграция.

В данной работе следует проверить коинтеграцию временных рядов используя критерий Энгла-Грэнжера. В данной работе следует проверить приводимый пример, незначительно изменив данные, провести вычисления и объяснить смысл применения критерия Энгла-Грэнжера.

Исходные данные и результаты расчетов сведены в таблицу (столбцы B,C,D).

В таблице даны: у - временной ряд зависимой переменной, х - временной ряд независимой переменной, е остатки от регрессии (чтобы получить данные об остатках необходимо активизировать параметр "вывод остатков" в окне задания условий функции РЕГРЕССИЯ пакета "Анализ данных" ). e(t-1) и е(t)-e(t-1) соответствующие модифицированные ряды от е. Далее получить новое регрессионое уравнение (аналогично предыдущему шагу), где зависимая переменная е(t)-e(t-1), а e(t-1) независимая. Значение t-статистики при 5% уровне значимости -2,60423, критическое значение статистики Энгла-Грэнжера при этом же уровне значимости 1,6177. По абсолютной величине фактические значения t-статистики превышают критические значения статистики Энгла-Грэнжера. С учетом оценки по критерию можно сделать вывод о коинтеграции рассматриваемых временных рядов.