Глава 4. Регрессионный анализ.

Тема 9. Регрессионный анализ статданных. Простая линейная регрессии. Оценивание параметров линейной регрессиии методом наименьших квадратов, коэффициент детерминации.

Простая линейная регрессия. На предыдущей лекции были рассмотрены основные понятия и методы корреляционного анализа, позволяющего решать задачи определения тесноты и направ­ления связи, существующей между изучаемыми величинами. Регрессионный анализ представляет собой следующий этап статистического анализа и позволяет предсказать значения случайной величины на основании значений одной или нескольких незави­симых случайных величин. Достижение этой цели оказывается возможным за счет определения вида аналитического выражения, описывающего связь зависимой слу­чайной величины (которую в этом случае называют результативным признаком) с не­зависимыми случайными величинами(которые называют факторами).

Форма связи результативного признака с фактораминазывается уравнением регрессии. В зависимости от типа выбранного уравнения различают линей­ную и нелинейную регрессию (например, квадратичную, логарифмическую, экспонен­циальную и т.д.).

Регрессия может быть парная (простая) и множественная, что определяется числом взаимосвязанных признаков. Если исследуется связь между двумя признаками (результативным и факторным), то регрессия называется парной (простой); к этому типу относится, например, исследование зависимости между продажами и затратами на рекламу. Если исследуется связь между тремя и более признаками, то регрессия называется множественной (многофакторной) - например, если исследуется связь между уровнем потребления, доходом, финансовым состоянием и размером семьи.

На этапе регрессионного анализа решаются следующие основные задачи:

1. Выбор общего вида уравнения регрессии и определение параметров регрессии.

2. Определение в регрессии степени взаимосвязи результативного признака и факторов, проверка общего качества уравнения регрессии.

3. Проверка статистической значимости каждого коэффициента уравнения рег­рессии и определение их доверительных интервалов.

Простая линейная регрессия.

Выбор общего вида уравнения регрессии является важной задачей, поскольку форма связи выявляет механизм получения значений зависимой случайной перемен­ной Y. Форма связи может быть линейной или нелинейной. Линейная связь описыва­ется линейным уравнением. Уравнение простой линейной регрессии имеет вид:

График этой функции называется линией регрессии. Линия регрессии точнее всего отражает распределение экспериментальных значений на диаграмме рассеяния, а угол ее наклона характеризует степень зависимости между двумя переменными.

Параметры уравнения регрессии могут быть определены с помощью метода наи­меньших квадратов. При опре­делении параметров модели методом наименьших квадратов минимизируется сумма квадратов остатков.

Для нахождения оценок параметров идоставляющих минимум функции, вычисляются и приравниваются к нулю частные производные этой функции=0 и=0,

откуда система нормальных уравнений принимает следующий вид:

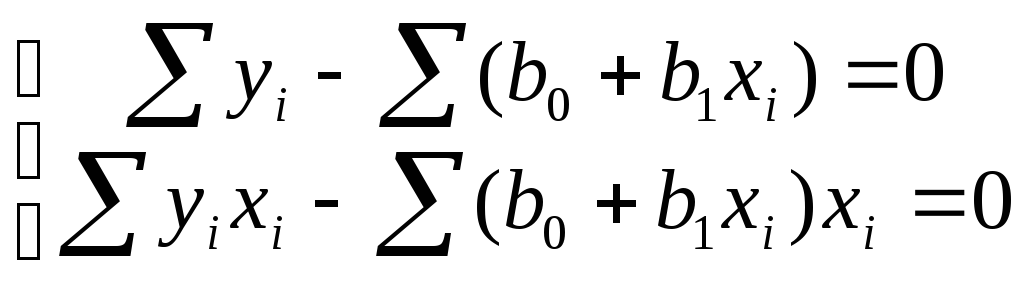
После простых преобразований имеем:

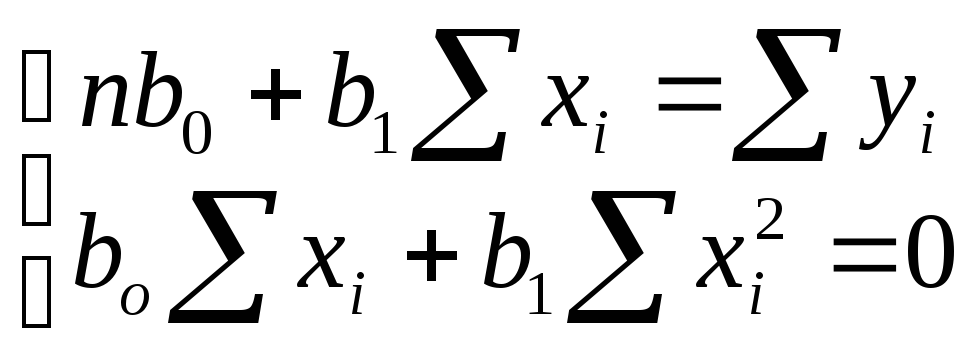
Тогда коэффициент наклона прямой регрессии равен:

а свободный член регрессии

.

Для свободного члена последнее равенство можно переписать следующим образом:

откуда . Это означает, что средняя точка (х, у) совместного распределения величин X, Y всегда лежит на линии регрессии. Поэтому при замененаполу­чается, т.е. среднеезаменяет.

Для анализа общего качества уравнения линейной регрессии используется коэффициент детерминации , который получается посредством возведения в квадрат коэффициента корреляции. Коэффициент детерминации показывает в какой мере изменчивость величины У объясняется поведением величины X. Haпример, если коэффициент корреляции совокупных данных, относящихся к производственным затратам, равняется 0,8, то коэффициент детерминации = 0,82 = 0,64. Это значение говорит о том, что 64% вариации (изменчивости) затрат объясняется количеством изделий, выпущенных за определеный период. Остальная часть (36%) общих затрат объясняется другими причинами.

Для расчета параметров уравнения линейной регрессии и проверки его адекватности исследуемому процессу в современных статистических пакетах имеются соответствующие функции и процедуры.

Литература:

1осн. [273-285], 2осн. [42-74], 6осн. [22-30], 2доп. [60-76], 3доп. [260-266], 4 доп. [135-142], 6доп. [206-214].

Контрольные вопросы

1. Какова основная задача регрессионого анализа статданных?

2. Какие могут быть формы связи между факторными и результативными признаками?

3. Каковы основные этапы регрессионного анализа?

4. Каким методом может быть найдено регрессионное уравнение?

5. Что отражает коэффициент детерминации?