mat_univer_ret (1)

интегралды еcепте:C) 2.D) .G) .

берілсе, тап:C) _{.E) .F)} .

берілсе, тап: B) .

берілсе, тап:D) .

берілсе, тап:D) 5.E) 10-.H).

интегралды еcепте:A) 3(e -1).D) 3e-3.G) -3+3e.

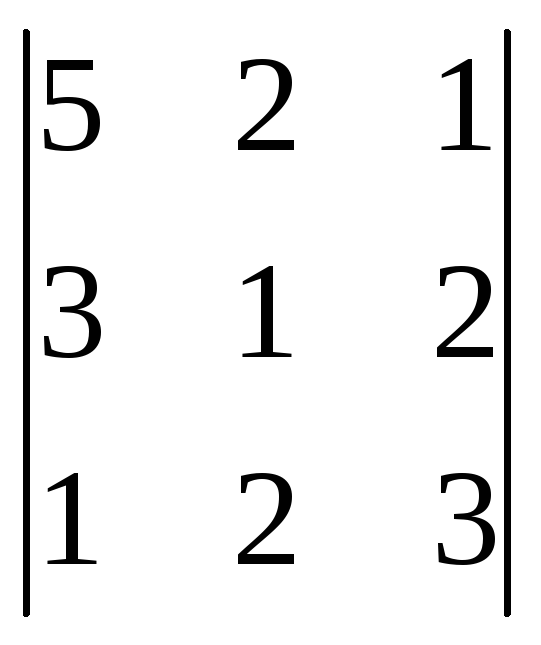анықтуышы үшін А13 алгебралық толықтауышын есептеңіз:A) .D) 5.G) 5lne.

берілген. табу керек:A) .C) .F) .

геометриялық мағынасы:A) Қисық сызықты трапецияның ауданы.

гиперболасының нақты жарты өсін табыңыз:C).D) 6.F) 12-.

дифференциалдық теңдеуінің жалпы шешімін табыңыз:A) .E) .

дифференциалдық теңдеуінің жалпы шешімін табыңыз:A) .F) .

дифференциалдық теңдеуінің жалпы шешімін табыңыз:E) .

есептеңіз, мұнда :A) 40.B) 1.E) 70.

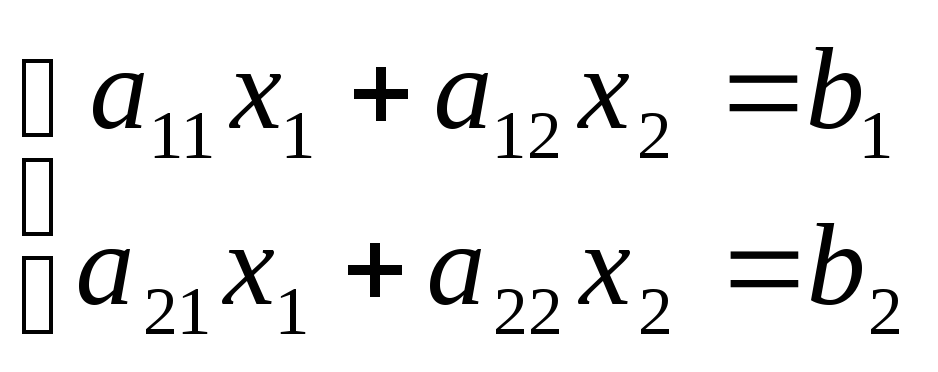жүйесін шешу үшін Крамер формуласын көрсетіңіз:B) ; .

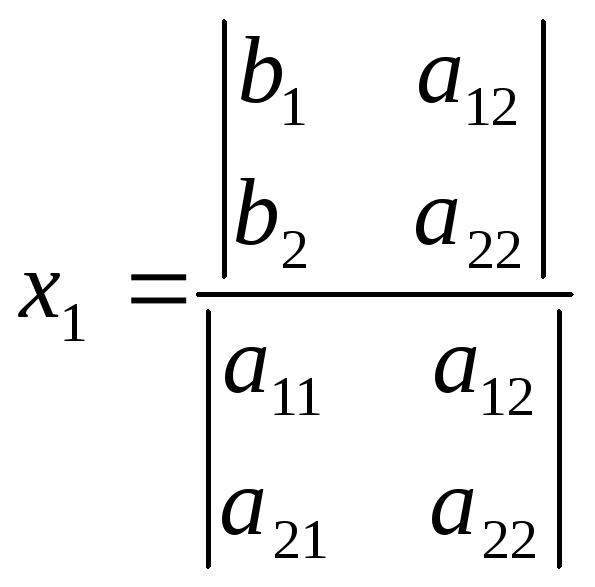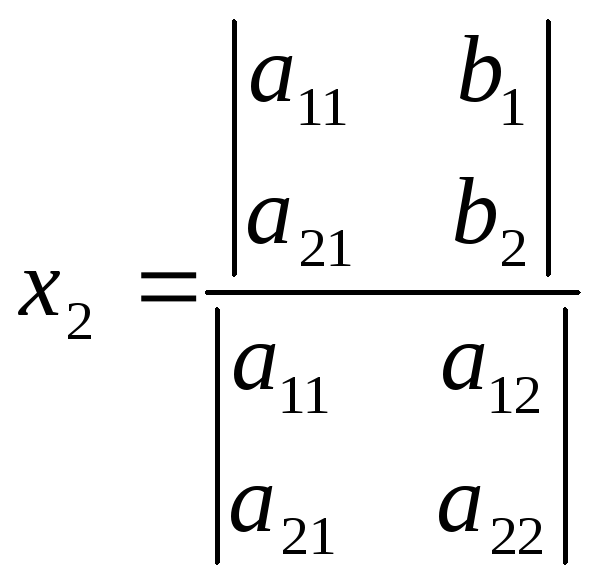интегралды е епте:C) .E) .H) .

интегралды еcепте: B) .D) .F) .

интегралды еcепте:A) .C) .

интегралды еcепте:A) .C) -.

интегралды еcепте:A) .D) .G) .

интегралды еcепте:B) .D) .

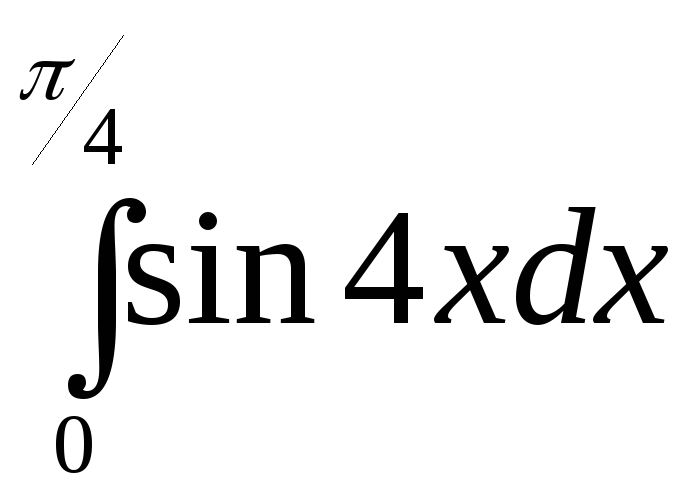интегралды еcепте:B) .E) 0,5.H) 2-1.

интегралды еcепте:B) ln (+1).D) ln (1 + ).

интегралды еcепте:C) + C .G) 0,2.H) 5-1.

интегралды еcепте:C) -e+ C.E) .H) .

интегралды еcептеA) arctg (x+2) + C .D) arctg (2+x) + C.F) 20 arctg (x+2) + C.

интегралын есептеңіз: C) 6.E) 2.G) .

неге тең:A) F(b)-F(a), где (x) = f(x).E) - F(a)+F(b), где (x) = f(x).

неге тең:B) 31ex + C.F) C+31ex.

нені белгілейді:A) Анықталған интеграл.

облысы бойынша дененің көлемі келесі формула бойынша есептеледі:B) .

сызықтарымен шектелген фигураның ауданын тап:A) 9/2.D) (2/9)-1.G) 4,5.

сызықтық тендеулер жүйесін шешініз:

функциясы үшін - ті тап:B) .E) .

функциясы үшін кризистік нүктелерін тап:A) –2 және 0.F) және 0.H) -2lne және 0.

функциясының максимум нүктелерін анықтау керек :B) -2lne.E) .F) .

функциясының өсу аралығын тап: A) (-∞; -1)  (3; ∞).D) .

функциясының туындысын есепте: A) .C) .

функциясының туындысын есепте: B) .C) .D) .

 матрицалардың көбейтіндісін есепте:A) .

+ матрицалардың қосындысын есептеніз:D) .G) .H) .

c={1,1,2} және d={2,1,0} векторларының скаляр көбейтіндісін табыңыз:B) 3.D) 3lne.E) .

c={2,4,4} және d={2,1,2} векторларының арасындағы бұрыштың cos табыңыз: B) cos  =8/9.E) cos  =23/32.

F(x) функциясы f(x) функциясы үшін алғашқы образ деп аталады, егер барлық х үшін. . . болса:D) F(x) = f(x).

f(x) функциясы өзінің анықталу облысындағы кез-келген х үшін жұп деп аталады, егер :C) f(-x)=f(x).E) f(x)=f(-x).

f(x) функциясы өзінің анықталу облысындағы кез-келген х үшін тақ деп аталады, егер:B) f(-x)=-f(x).E)- f(x)=f(-x).

y= - функциясы үшін вертикаль асимптотаның теңдеуін жаз:A) x=1.C) x-1=0.D) 1-x=0.

y=4-x2, y=0 сызықтарымен шектелген фигураның ауданын тап:A) 32/3. D) .F) .

y=f(x) функциясының x=x0 нүктесіндегі туындысы мынаған тең:D) y=f(x) функцмясына (x0,f(x0)) нүктесінде жүргізілген жанаманың көлбеулік бұрышының тангенсіне тең.

А квадрат матрицасы ерекше деп аталады, егер:A) detA=0.E) detA=ln1.H) detA=lne-100.

А квадрат матрицасы ерекше емес деп аталады, егер:C) detA≠0.

А(2,-3) және В(-1,7) нүктелерінің ара қашықтығын табыңыз:B) 5.E) .F) 10-.

Ақиқат оқиғаның ықтималдығы:A) .F) p=lne.G) p=100.

Бернулли формуласы:D) .

болатындай А және В сандарын тап :A) A = 1, B = -1.D) A = 20, B = -1.

Бөліктеп интегралдау формуласы: B) .F) .

Бірінші тамаша шектің формуласы:A) .F) .

векторының ұзындығын табыныз:C) 7.F).H)14-.

Егер болса, тап:D) .F) .

Егер болса, y’ есепте:A) 2cos 2x.C) –2(- cos2x).

Егер y(x)=ln(3x) болса, табу керек: A)- .C) .G) .

Егер анықтауыштың екі жолын орындарымен ауыстырсақ, онда:A) Анықтауыштың таңбасы өзгереді.

Егер беттің теңдеуі түрінде берілсе, онда нүктесінде жанама жазықтығының теңдеуі мына түрде болады:A) .

Егер беттің теңдеуі түрінде берілсе, онда нүктесіндегі нормаль жазықтығының теңдеуі мына түрде болады :B) .

Екі жолы өзара пропорционал анықтауыш:A) Нөлге тең.

Интегралды еепте :A) .D) .F) .

интервалында сызықтарымен шектелген фигураның ауданы қай формуламен есептеледі:D) .F) .

Кездейсоқ оқиғаның қабылдайтын мәні:B) .F) .H)0.

Келесі анықтауыш үшін М12 - минорды есепте 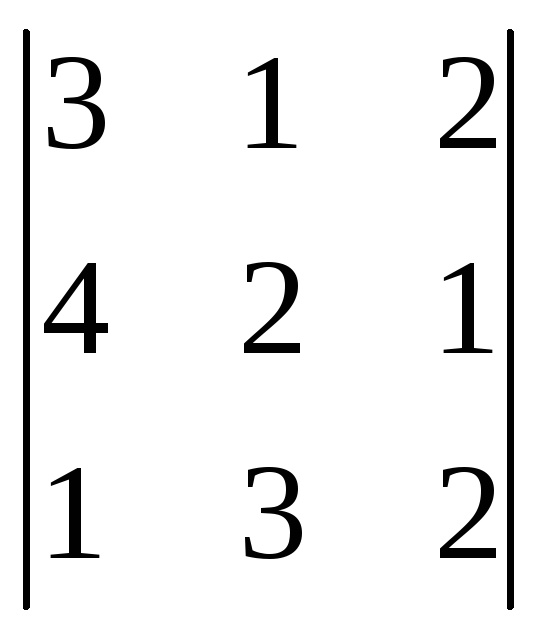:A) 7.F).H)14-.

Келесі анықтауышты есепте :B) 1.D) 100.G) lne.

Келесі анықтауышты есепте 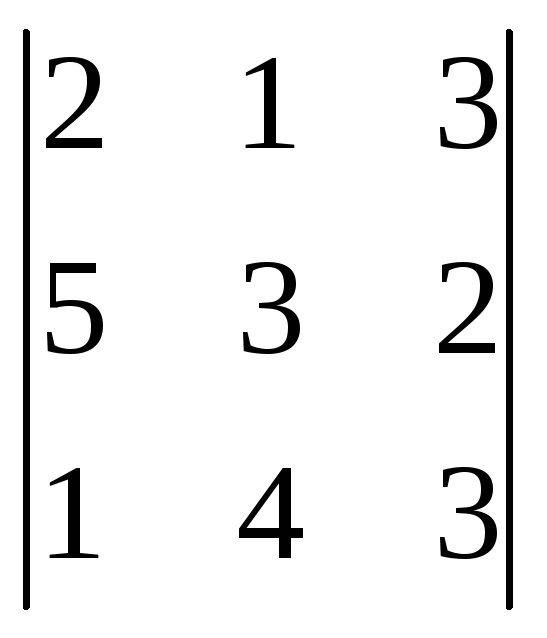:C) 40.G).H) 40lne.

Қандай векторлар коллинеар:C) c={-2,1,-3}, d={4,-2,6}.G) c={2,-1,3}, d={4,-2,6}.

Қарама-қарсы оқиғалардың ықтималдығы:B) .H) .

М нүктесі АВ кесіңдісінің ортасы, А=(2, 7, 6) М=(3, 1, 7). В нүктесінің координаталары қандай:A) B=(, -5, .E) В=(4, -5, 8).H) B=(.

М(1,1) нүктесінен 3х+4у-2=0 түзуіне дейінгі ара қашықтықты табыңыз:D) 1.E) 50.H) lne.

М1(2, -5) және М2 (3, 2) нүктелері арқылы өтетін түзудің бұрыштық коэффициенті қандай :B) .E) 7.G) 14-.

Математикалық күтімнің қате жазылған қасиеті:F) .G).H).

Меншіксіз интегралды есептеңіз :C) .

Мүмкін емес оқиғаның ықтималдығы:D) .E) .H) p=1-50.

Ортогональ векторларды анықтаныз:A) c={-1,0,2}, d={0,6,0}.D) c={1,1,3}, d={1,2,-1}.F) c={0,1,2}, d={1,4,-2}.

ОХ осінен айналдырғанда шығатын айналу денесінің көлемі :A) .C) .

Р-ның қандай мәнінде түзуі түзуіне параллель болады:B) 2.E) .H) log24.

Сандық қатар жинақталады дейміз, егер: C) .

Тәжірибенің, алдын ала болжап білуге болмайтын нәтижесі:C) Кездейсоқ оқиға.

Тәуелсіз оқиғалардың ықтималдықтарын көбейту формуласы:A) .

Төмендегі векторлардың қайсысы 3х-у+2z-5=0 жазықтығының нормаль векторы болады:B) .

Төмендегі сандардың қайсысы эллипстің эксцентриситеті бола алады:A) 0,2.D) 0,5.H) 1/5.

Үйлесімсіз оқиғалардың ықтималдықтарын қосу формуласы:A) .

Функция өсімшесінің у=f(x0+x)-f(x0) аргумент өсімшесі x-ке x-тің нөлге ұмтылғанда қатынасының шегі:B) f(x) функциясының туындысы.

функциясының туындысын есепте:B) .D) .H) .

Х дискретті кездейсоқ шаманың математикалық күтімінің формауласы:C) .

Х кездейсоқ шамасының дисперсиясының формуласы:D) .F).

Х үзіліссіз кездейсоқ шаманың математикалық күтімінің формауласы:A) .

Шекті есепте :A) .C) -0,6.E) .

Шекті есепте :A) .C) 2-1.E) 0,5.

Шекті есепте :A) .D) .H) .

Шекті есепте :A) 1 .E) lne.G) 20.

Шекті есепте :A) e2 .C) .F) .

Шекті есепте :B) 2a.D) .F) .

Эллипстің кіші жарты осі 24, ал фокустар қашықтығы 2с=20. Эллипстің үлкен жарты осін табыңыз:C) 26.E) .G) .