5.2.2. Алгоритм Джарвиса

Анализируя свойства выпуклой оболочки можно заметить, что если провести прямую по ребру принадлежащему оболочке, все вершины множества окажутся по одну сторону от этой прямой или на самой прямой (свойство). Используя это свойство можно выделитьребер, удовлетворяющих заданному критерию, а затем расставить их в порядке следования. Очевидно, в худшем случае. Джарвис предложил алгоритм, несколько оптимизирующий указанный выше способ. Алгоритм Джарвиса обходит выпуклую оболочку, порождая в нужном порядке последовательность крайних точек, по одной на каждом шаге. Этот процесс очень напоминает заворачивание предмета в бумагу, поэтому он имеет также другое название - «заворачивание подарка».

Выбор вершин выпуклой оболочки ведется по некоторому критерию, сохраняющему свойство . Рассмотрим следующую последовательность операций:

1. Найдем точку (обозначим ее ), которая заведомо будет принадлежать выпуклой оболочке (например, самую правую точку с минимальной координатой поy) и запомним ее.

2. Пусть построена последовательность вершин выпуклой оболочки. В качестве точкивыберем нерассмотренную к этому моменту вершину, имеющую наименьший полярный угол относительно

3. Повторим шаг 2 для второй и последующих точек выпуклой оболочки до тех пор, пока в оболочку не будет включена вершина с максимальным значением у-координаты.

4. Далее начинается обратный проход, который повторяет шаг 2 с единственной ремаркой: при сравнении полярных углов необходимо искать минимальный относительно отрицательного направления оси абсцисс.

Пример отбора точек при обходе Джарвиса показан на рисунке:

Оценим время работы этого метода. Для каждой вершины выпуклой оболочки находятся полярные углы всех остальных точек (это требует времени), и среди этих полярных углов ищется минимальный (еще). Нетрудно видеть, что данный процесс напоминает сортировку простым выбором минимального элемента! Если оболочка состоит източек, то время работы равно²⁶. Наихудшим будет случай, когда все точки исходного множества принадлежат выпуклой оболочке. В этом случае время работы метода составит.

Как следует из анализа сложности алгоритма, для худшего случая алгоритм Джарвиса затрачивает больше времени, чем алгоритм Грэхема. Однако, если число вершин выпуклой оболочки невелико (или является медленно растущей функцией (медленнее, чем )), то алгоритм Джарвиса в этом случае является более предпочтительным.

5.2.3. Метод разделяй и властвуй.

Поскольку задача построения выпуклой оболочки легко разбивается на подзадачи, можно для ее решения применить технику «разделяй и властвуй». Разобьем множество източек на два подмножестваипоиточек в каждом соответственно. После разбиения можно рекурсивно строить выпуклую оболочку для каждого из множестви. Для построениянеобходимо решить задачу слияния оболочеки. С этой целью выберем некоторую внутреннюю точкумножества. Например, в качествеможно взять центроид трех любых вершин, лежащих на. Далее рассмотрим следующие варианты:

1. точка является внутренней вершиной в. Условие выполняется, если при обходе вершин изпротив часовой стрелки, вершинавсе время лежит слева от ребер соответствующего многоугольника. Данная процедура занимаетвремени. Поскольку вершиныиявляются упорядоченными по полярному углу относительно точки, можно, используя метод Грэхема, построить завремени выпуклую оболочку для множества. Эта ситуация проиллюстрирована на рисунке ниже

2. точка не является внутренней вершиной в.Поместим в точкуточечный источник света, который «освещает» точки из. Извыходят два луча (опорные прямые), касающиеся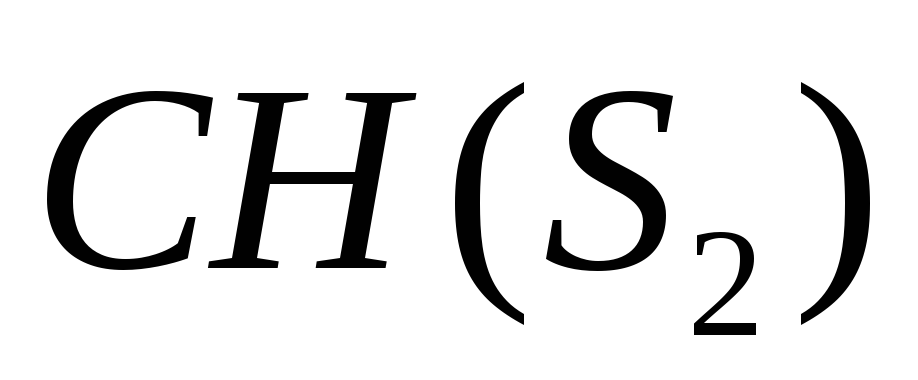в точкахи. Тогда цепь, составляющая, разбивается точкамиина освещенную и затененную части. При движении против часовой стрелке вокруг точкиот точкикпо затененной части полярный угол возрастает, а такое же движение откпо освещенной части вызывает уменьшение значения угловой меры. Можно не рассматривать вершины освещенной части цепи, поскольку они являются внутренними точками множества. Затененная часть границыи граница множествапредставляют собой два упорядоченных списка, которые содержат в общей сумме не болеевершин. После слияния этих последовательностей (требует не болеевремени), применяем к получившейся последовательности метод Грэхема и строим

Обозначая время работы алгоритма на точках черези учитывая, что построение опорных прямых требуетвремени, имеем следующие рекуррентные соотношения

где - некоторые константы. Решением этого уравнения является функция

Метод разделяй и властвуй имеет много общего с алгоритмом сортировки слиянием. Идеи, заложенные в алгоритме Quicksort, нашли отражение в методе построения выпуклой оболочки, названном