5.1.2. Относительный покой

Пусть жидкость находится в открытом сосуде и вращается с угловой скоростью  около своей вертикальной оси (рис. 5.2).

Когда движение установится, жидкость будет вращаться вместе с сосудом и будет относительно последнего находиться в покое. Лабораторную систему отсчёта свяжем с вращающимся сосудом.

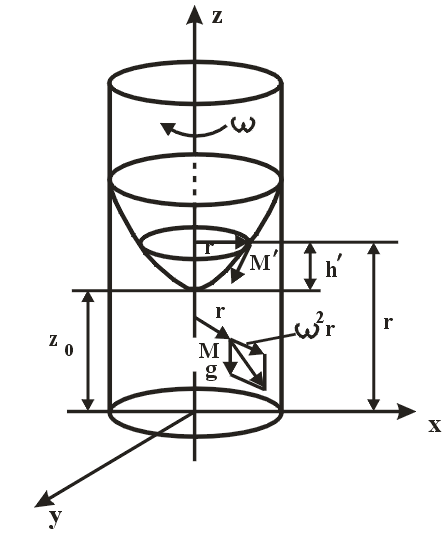
Рис. 5.2. Относительный покой жидкости во вращающемся сосуде

Из массовых сил на каждую частицу жидкости, например М, будут действовать сила тяжести и центробежная сила инерции, вызванная вращательным движением сосуда:

для силы тяжести: ,

(5.16)

для центробежной силы инерции: ,

где x,y,z - координаты точки М (рис. 5.2).

Для определения поверхности равного давления во вращающемся сосуде воспользуемся дифференциальным уравнением (5.4). Получаем:

, (5.17)

откуда после интегрирования находим:

. (5.18)

Уравнение (5.18) показывает, что поверхности равного давления представляют параболоиды вращения.

Для определения свободной поверхности, то есть поверхности соприкосновения жидкости с газом, можно сделать предположение, что она также будет являться поверхностью равного давления, а именно давления газа над ней р₀. Для получения соответствующего уравнения надо найти значение C₀. Учитывая, что при z = z₀, где z₀ расстояние от вершины параболоида до днища сосуда, x = 0, y = 0, получим:

.

Окончательно, с учетом, что r² = x² + y² , получим:

. (5.19)

По этому уравнению можно найти любую точку, например, М' (радиус r) на свободной поверхности.

Точка М' находится над уровнем z₀ на высоте h', равной

, (5.20)

где w =  r - линейная скорость точки М'.

Приведенные ранее уравнения позволяют найти закон распределения давлений. Используя формулу (5.3) и, учитывая преобразования, сделанные при выводе уравнения (5.17), получаем:

. (5.21)

Интегрируя, получаем:

. (5.22)

Учитывая, что r² = x² + y² , полученное уравнение приводим к виду:

. (5.23)

Постоянную C₁ находим по давлению р₀ в точке свободной поверхности, расположенной на оси z (r = 0) и координата которой z = z₀. Тогда

,

. (5.24)

5.2. Характеристики движения сред

Поток жидкости. Под потоком жидкости подразумевают движение среды жидкости, ограниченной поверхностями раздела фаз.

Можно указать следующие примеры потоков:

- поток в реке, который ограничен неподвижным ложем реки и свободной поверхностью жидкости, соприкасающейся с воздухом;

- поток в трубе, полностью заполненной жидкостью, ограничен твердыми стенками трубы;

- струя, вытекающая из отверстия в стенке сосуда, представляет собой пример потока, ограниченного лишь свободной поверхностью жидкости, соприкасающейся с газом,

Установившееся и неустановившееся движение.

Установившимся (стационарным) движением является такое, когда скорости частиц потока, а также все другие, влияющие на его движение величины (плотность, температура, давление и др.) не изменяются во времени в каждой фиксированной точке пространства. При таком движении любая из указанных величин, например, скорость w_х в некотором направлении x может иметь различное значение в разных точках w_х = f(x,y,z), но в любой точке скорость не изменяется со временем, т.е. w_х / t = 0.

При неустановившемся (нестационарном) потоке, величины, характеризующие движение, изменяются во времени в фиксированной точке пространства. Так скорость среды в направлении x в любой точке является не только функцией пространственных координат x,y,z данной точки, но также времени t, т.е. w_х = f(x,y,z,t), при этом w_х/t не равно нулю.

Равномерное и неравномерное движение - это два вида установившегося движения потока.

Равномерное - это такое движение, когда форма и площадь поперечного сечения, а также средняя скорость по длине прямолинейного потока жидкости являются постоянными.

При неравномерном движении, площадь поперечного сечения и средняя скорость меняются по длине потока.

Напорное и безнапорное движение. Напорным движением называется такое движение, когда поток ограничен твердыми поверхностями и не имеет свободной поверхности, т.е. поперечное сечение канала полностью заполнено жидкостью. Напорное движение происходит вследствие наличия разности давлений по длине потока, создаваемой, например, насосом, водонапорной башней и т.д.

Безнапорным движением называется такое, когда поток не со всех сторон ограничен твердыми стенками, а имеет свободную поверхность. В этом случае движение, в частности, может быть вызвано уклоном канала, по которому движется жидкость и происходит при неизменном по длине канала давлении.

Линия тока. Линия тока представляет собой линию, в каждой точке которой в данный момент времени вектор скорости жидкости касателен к этой линии (рис. 5.3).

Рис. 5.3. Линия тока А - А₁ - А₂

При установившемся движении жидкости линии тока и траектория движения частиц жидкости, на них расположенных, совпадают. При неустановившемся движении линии тока и траектории различны между собой, т.к. каждая частица находится на данной линии тока лишь одно мгновение, да и сама линия тока в общем случае существует одно мгновение.

Средняя скорость, поперечное и живое сечения потока. Поле конвективной скорости потока может иметь сложный характер. Даже в простейшем случае ламинарного стабилизированного течения среды в прямой цилиндрической трубе, когда все слои движутся параллельно в одном направлении, как будет показано ниже, скорости в различных точках потока имеют различные значения (рис. 5.7). Выбрав произвольное плоское сечение можно найти среднюю по площади данного сечения S скорость

. (5.25)

Если вектор средней скорости окажется перпендикулярен выбранному плоскому сечению, то такое сечение называют поперечным сечением потока. Понятно, что для случая течения в прямой трубе поперечное сечение будет перпендикулярно оси трубы. В более сложных случаях, например, в случае изогнутой трубы определение площади поперечного сечения и средней скорости представляет значительно большую сложность.

Живым сечением потока называют поверхность, нормаль к которой в каждой точке совпадает с направлением локальной конвективной скорости. В простейшем случае однонаправленного движения живое сечение идентично с плоским поперечным сечением. В общем случае живое сечение может представлять собой поверхность сложной формы.

Массовый и объемный расходы потока. Уравнение постоянства расхода. Масса жидкости, протекающая через поперечное сечение потока S в единицу времени, называется массовым расходом. Объем жидкости, протекающий через поперечное сечение потока S в единицу времени, называется объемным расходом:

, (5.26) , (5.27)

где G - массовый расход, кг/с; - средняя по поперечному сечению S скорость; - объемный расход, м³/с;

Из уравнения неразрывности для установившегося движения (2.22) или закона сохранения массы в интегральной форме (2.3) следует уравнение постоянства расхода (2.24):

. (5.28)

Рис. 5.4. Трубопровод переменного сечения

Для трех различных сечений трубопровода на рис. 5.4 (1,2,3) имеем

или

.

Отсюда следует, что для установившегося движения при увеличении площади поперечного сечения потока его средняя скорость уменьшается, и наоборот.

Геометрические элементы потока. Основными геометри­ческими элементами потока являются площадь поперечного сечения потока S, смоченный периметр П_с, гидравлический радиус r_г, эквивалентный диаметр d_э.

Смоченным периметром П_с называется длина контура поперечного сечения, по которому жидкость соприкасается со стенкой. Гидравлический радиус r_г представляет собой отношение площади поперечного сечения потока к смоченному периметру:

. (5.29)

Эквивалентный диаметр связан с r_г и равен

. (5.30)

Идеальная жидкость, виды напора. Идеальной жидкостью называется несжимаемая среда, движущаяся без трения. Для установившегося прямолинейного потока идеальной жидкости в любом поперечном сечении поле скорости будет однородным т.е. локальные скорости будут совпадать со средней. В этом случае для всего потока выполняется уравнение Бернулли (2.38), являющееся законом сохранения механической энергии. Поделив уравнение (2.38) на ускорение свободного падения g, его можно представить в виде

. (5.31)

Величину H называют полным или гидродинамическим напором. Из (6.31) следует, что гидродинамический напор для любых поперечных сечений потока идеальной жидкости, например, 1 и 2, должен оста­ваться неизменным

. (5.32)

Составляющие полного гидродинамического напора носят следующие названия: h = h_г - нивелирная высота (нивелирный, или геометрический напор); -пьезометрический, или статический напор; -полный гидростатический напор или просто гидростатический напор; -скоростной, или динамический напор. Все члены уравнения (5.32) имеют размерность длины и выражают удельную энергию, отнесенную к единице веса среды. Физический смысл их следующий: h_г - удельная потенциальная энергия положения относительно некоторой горизонтальной плоскости сравнения; h_ст - удельная потенциальная энергия давления; h_гс - полная удельная потенциальная энергия; h_ск - удельная кинетическая энергия; H - полная удельная механическая энергия.

Уравнение Бернулли можно переписать в ином виде, умножив члены уравнения (2.38) на плотность  или (5.31) на

. (5.33)

Каждый член этого уравнения имеет размерность давления и характеризует энергию единичного объема среды.

Реальная жидкость, потерянный напор, гидравлическое сопротивление, коэффициенты гидравлического сопротивле­ния. При движении реальной жидкости часть энергии затрачивается на работу по преодолению сил вязкого трения А_тр, в результате чего механическая энергия переходит в тепловую. Этот процесс необратим и носит название диссипации энергии. Потери механической энергии называются гидравлическим сопротивлением. Уменьшение механической энергии за счет гидравлического сопротивления, отнесенное в весу среды, носит название потерянного напора h_п. С учетом этого, уравнение (5.32) можно записать для реальной жидкости в виде

, (5.34)

где h_п,1-2 - потерянный напор на участке между сечениями 1 и 2. Учитывая, что в реальной жидкости поле скоростей неоднородно, в уравнении (5.34) использованы пьезометрический, скоростной и геометрический напоры осредненные по поперечным сечениям 1 и 2.

Для реальной вязкой жидкости можно записать аналог уравнения (5.33):

. (5.35)

В этом случае гидравлическое сопротивление на участке 1 - 2 характеризуется потерянным давлением р_n,1-2. Нетрудно убедиться, что потерянные напор и давление связаны простым соотношением

. (5.36)

Следует отличать потерянное давление р_n,1-2 от перепада давлений в сечениях 1 и 2 р_1-2 = р₁ - р₂. В частном случае горизонтального движения потока с постоянной средней скоростью эти величины будут совпадать, как это следует из (5.35). Однако в общем случае, как видно из того же соотношения, они отличны. Так, например, при стабилизированном течении пленки жидкости по твердой вертикальной поверхности под действием силы тяжести (безнапорное течение) перепад давлений р_1-2 = 0, а потерянное давление, равное , отлично от нуля, так как при этом наличествует гидравлическое сопротивление.

Отношение потерянного напора h_п к скоростному h_ск носит название коэффициента гидравлического сопротивления :

или (5.37)

. (5.38)

Потерянный напор можно представить в виде суммы потерь механической энергии на трение по длине прямолинейного участка потока h_тр, на котором движение происходит с постоянной по величине и направлению средней скоростью, и участках потока, на которых происходит изменение средней скорости по величине или направлению h_м.с. (местные сопротивления):

или (5.39)

. (5.40)

В соответствии с этим выделяют и коэффициенты гидравлического сопротивления трению _тр и коэффициенты местных сопротивлений _м.с. В свою очередь, _тр представляют в виде

, (5.41)

где _г - коэффициент гидравлического трения, - длина прямолинейного участка,d_э -эквивалентный диаметр.

Потерянное на трение давление р_тр можно выразить через поток импульса на границах или коэффициент импульсоотдачи. Потерянное давление или уменьшение механической энергии единичного объема есть работа против сил вязкого трения, отнесенная к единице объема:

. (5.42)

Работа есть произведение силы на длину пути в направлении действия силы, а есть сила трения, действующая на единицу поверхности, ограничивающую поток. С учетом вышесказанного для прямолинейного равномерного течения в направлении осиХ можно записать

. (5.43)

На рис. 5.5 дана геометрическая интерпретация уравнения (5.34).

Благодаря тому, что все члены уравнения Бернулли в записи (5.34) имеют размерность длины, зависимость между отдельными членами уравнения наглядно изображается графически (рис. 5.5).

На рисунке обозначены средние величины:

- нивелирные высоты (геометрические напоры) для сечений 1,2,3;

- пьезометрические (статические) напоры для тех же сечений;

- скоростные напоры;

h_n1-2 , h_n1-3 - потери напора между сечениями 1-2 и 1-3 соответ-ственно.

Рис. 5.5. Изменение различных видов напора при течении реальной жидкости

Линия О'-О' является линией гидродинамического напора для случая движения идеальной жидкости; в данном случае она дает возможность наглядно показать величины потерянного напора между сечениями 1-2 и 1-3.